Circunferencias tangentes a otra de centro conocido y a una recta conociendo el punto de tangencia
Para éste tipo de problemas conocemos una recta r tangente, una circunferencia dada y un punto de tangencia T determinado. Lo que se nos pide es hallar las dos circunferencias que son tangentes a la que se nos proporciona y a la recta dada. Este ejercicio ya se vio en las tangencias correspondientes a primero de bachillerato, donde lo resolvíamos usando las propiedades de las tangencias. Tu punto de partida debe ser semejante a esto:
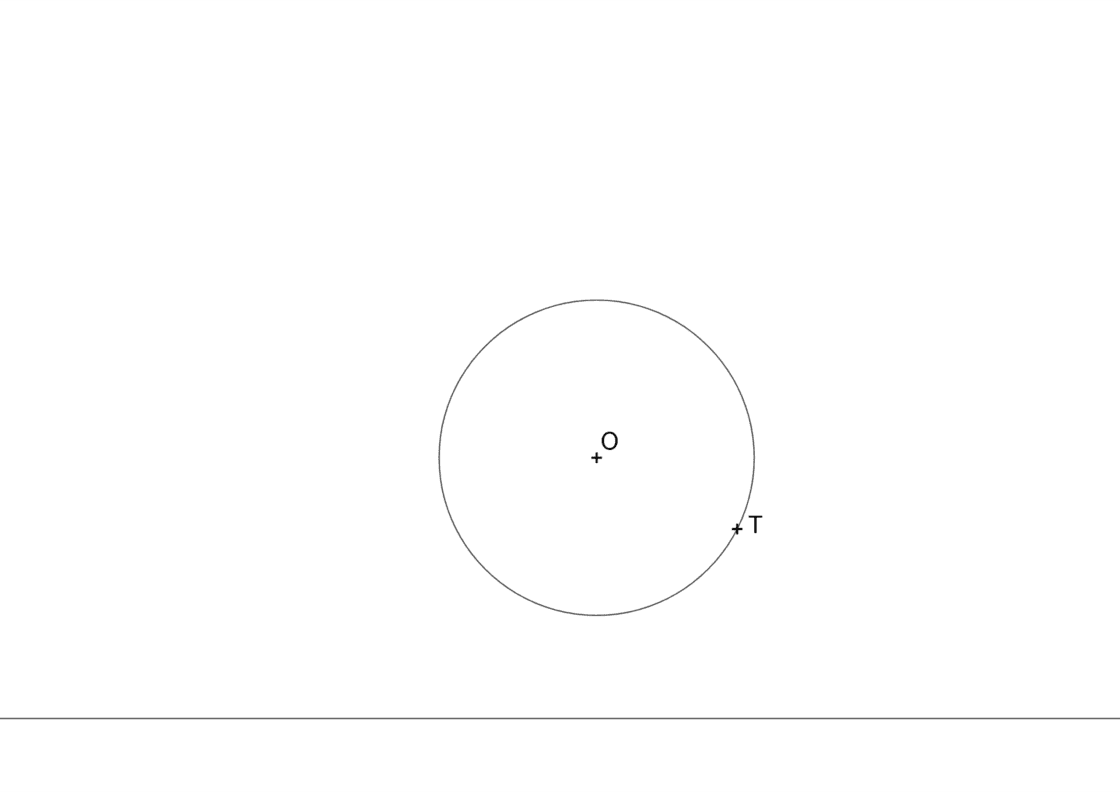
Para resolverlo procederemos de la siguiente manera:
Trazamos la recta tangente a la circunferencia dada por el punto de tangencia T que conocemos. Si prolongamos esta recta, obtendremos el punto C, que es el centro radical de las tres circunferencias.
Con centro en C y radio CT trazamos un arco de circunferencia que corta a la recta en los puntos T1 y T2. Si trazamos perpendiculares desde T1 y T2, encontraremos los centros de las circunferencias tangentes que se nos solicita sobre la prolongación del segmento que forman O y T.
Como puedes ver, tendrás dos circunferencias. Una de ellas contendrá a la circunferencia inicial, y la otra será exterior.
Otra variante posible… conociendo el punto de tangencia sobre la recta
Este tipo de problemas son similares al planteamiento del ejercicio anterior, pero en ésta ocasión conocemos el punto de tangencia sobre la recta. Por lo tanto tu punto de partida se parecerá a esto:
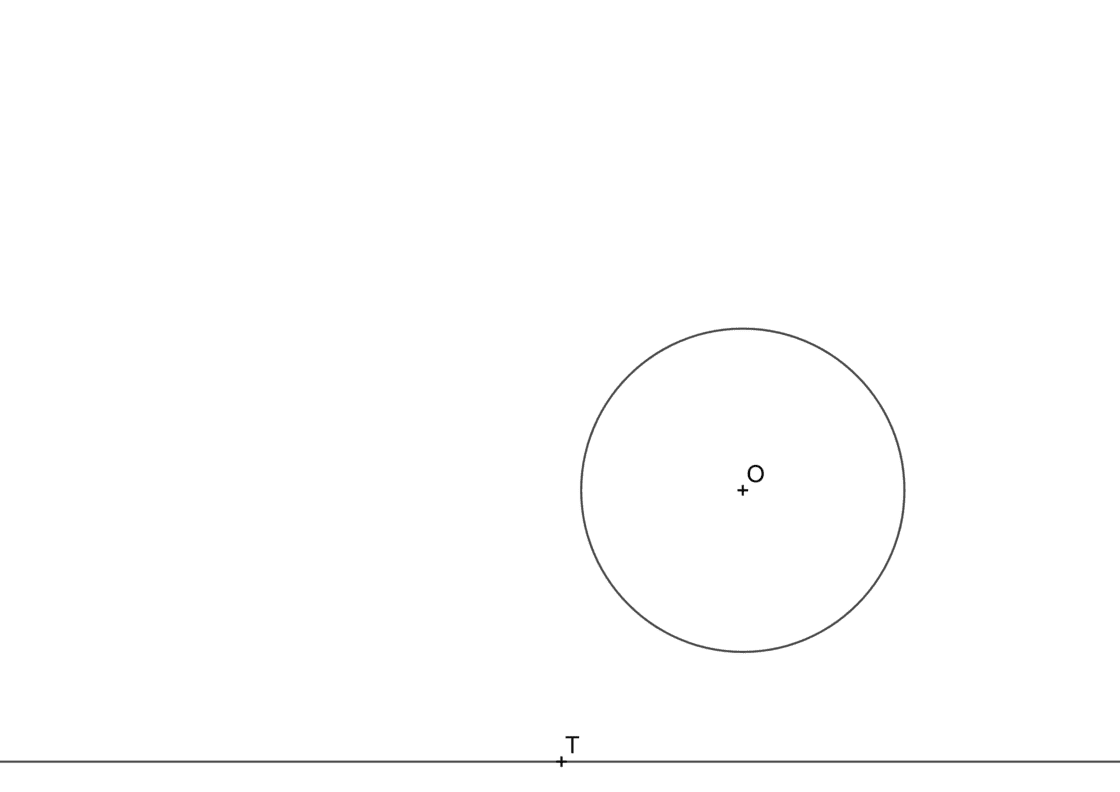
Aquí tienes el vídeo con el desarrollo detallado del ejercicio, y más abajo la descripción detallada paso a paso.
Para empezar, trazaremos una perpendicular a la recta r que conocemos a partir del punto de tangencia T1 que conocemos. Los centros de las circunferencias tangentes que buscamos se encontrarán sobre ésta perpendicular.
Sobre esta perpendicular que acabamos de trazar, dibujamos una circunferencia auxiliar con centro en cualquier parte de dicha perpendicular, al que llamaremos O2, y radio O2T. De ese modo obtenemos dos puntos de corte A y B sobre la circunferencia inicial que conocíamos de centro O1.
La recta que une A y B es el eje radical de las circunferencias de centro O y O1. Si prolongamos la recta que pasa por A y B hasta cortar sobre la recta r, obtendremos el centro radical Cr de la recta y las dos circunferencias de centro O y O1. Desde Cr trazaremos ahora las rectas tangentes a la circunferencia inicial de centro O1 hallando los puntos de tangencia T1 y T2
Para hallar los centros de las circunferencias tangentes buscadas solo tenemos que unir el centro de la circunferencia inicial dada O1 con T2, y en su prolongación tendremos el centro O3 al cortar con la perpendicular a r que pasa por T1. Del mismo modo, si unimos T3 con O1, en su prolongación hallamos O4 en el punto de corte con la perpendicular a r que pasa por T1.
Circunferencias tangentes a dos rectas que se cortan y pasan por un punto dado
Para este tipo de ejercicios conoces dos rectas secantes y un punto contenido entre ellas por el que deben pasar las dos circunferencias tangentes. Tu punto de partida debe ser parecido a esto:
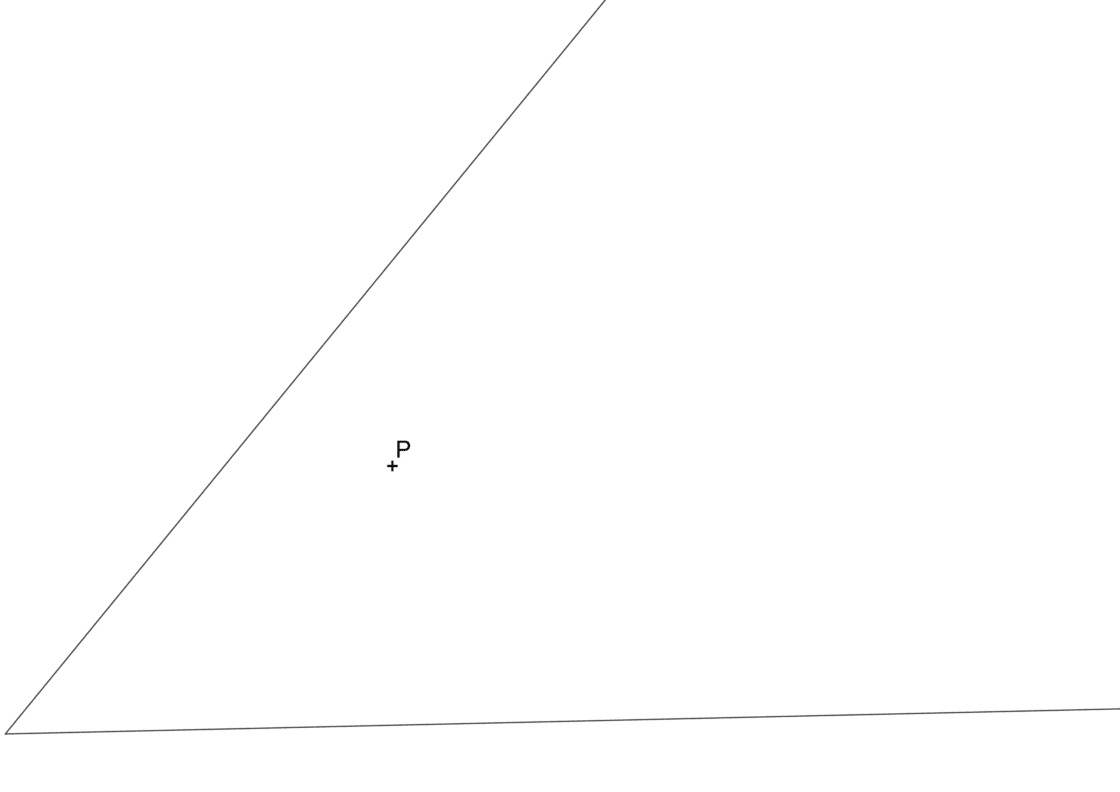
En el siguiente vídeo podéis ver todo el proceso de forma fácil y clara. Y justo debajo tenéis la transcripción.
Partimos de la base de una determinada información que conocemos. En éste caso, conocemos dos rectas concretas que denominaremos r y s. También conocemos un punto de corte que ambas circunferencias tienen en común al que llamaremos P.
Éste ejercicio es más sencillo de lo que en un principio pudiera parecer. En primer lugar, debemos recordar que la bisectriz del ángulo que forman las dos rectas contiene los centros de ambas circunferencias. Partiendo de ésta base, en primer lugar trazaremos dicha bisectriz.
En segundo lugar, trazaremos una perpendicular a dicha bisectriz que pase por P. De ese modo podemos hallar P’, que se encuentra sobre esa perpendicular separada de la bisectriz por la misma distancia que P. Prolongamos esta perpendicular para hallar un punto de corte con una de las dos rectas, en éste caso A, que utilizaremos más tarde. Si te das cuenta, esta recta es el eje radical de las dos circunferencias que estamos buscando, y el punto de corte A, en realidad es el centro radical de estas dos circunferencias con la recta que ha cortado.
Trazamos una circunferencia auxiliar con centro en un punto cualquiera sobre la bisectriz al que vamos a llamar O1 y que pase por P y P’. Acto seguido hallaremos una recta que pase por A y sea tangente a dicha circunferencia auxiliar, hallando el punto T.
Para terminar, con centro en A y radio AT, trazamos una semicircunferencia para hallar los puntos donde las circunferencias tangentes tocan a la recta que contiene A. Estos puntos los llamaremos T1 y T2
Resolución dada una recta y los dos puntos de corte
En este caso el planteamiento es ligeramente distinto. Se nos proporciona una recta de tangencia r y los dos puntos donde dichas circunferencias se cortan entre si que llamaremos P y P’. Para este tipo de problemas podemos encontrar dos posibles opciones. En la primera de ellas, ambas circunferencias se encuentran en el plano. Esta tiene una solución mucho más fácil. En la segunda opción una o ambas circunferencias son tan grandes que no pueden ser contenidas en el plano.
Trazando dos perpendiculares a partir de dichos puntos hallaremos los puntos de corte con la bisectriz, que determinan los centros de ambas circunferencias tangentes.
Veamos como resolver ambas situaciones.
Caso 1: Las circunferencias tangentes están dentro del plano
Para este tipo de ejercicios la mediatriz entre los puntos P y P’ determina un ángulo agudo bastante cerrado con la recta de referencia. Tu punto de partida es semejante a esto:

En primer lugar trazaremos el segmento que une P con R y prolongaremos dicho segmento hasta cortar con la recta r hallando el punto A.
A continuación hallaremos la mediatriz del segmento PR, y en el punto donde corte A con la recta r tendremos el punto donde las rectas que contienen a las circunferencias se cortan.
Trazamos el reflejo de la recta r sobre la mediatriz, obteniendo la recta s. El resto del problema se resolverá como en el caso anterior.

Aquí abajo tienes la solución completa.
Caso 2: Cuando las circunferencias tangentes no están en el plano
En éste caso, una o ambas circunferencias tangentes no están contenidas en su totalidad dentro del plano de trabajo. Solo se puede visualizar parte de ellas. Tu punto de partida es algo similar a esto:

Para su resolución procederemos de la siguiente manera:
Unimos P y R y prolongamos éste segmento hasta su corte con la recta r, hallando así el punto A. Sobre esa mediatriz trazamos una circunferencia cualquiera con centro O1, que pase por P y R
Hallamos la recta que pasa por el punto A y es tangente a la circunferencia que acabamos de trazar, obteniendo el punto T1
Trazamos un arco con centro en A y radio igual al segmento AT1, que corta a la recta r en los puntos T2 y T3 que corresponden con los puntos de tangencia de las circunferencias tangentes que buscamos.
Para terminar, levantamos perpendiculares a la recta r desde los puntos T2 y T3. Los puntos donde dichas perpendiculares cortan a la mediatriz de PR serán los centros de esas circunferencias.
Conocidas dos rectas tangentes y a una tercera circunferencia de centro O1
En este caso, como explica el enunciado, tienes dos rectas secantes y una circunferencia interior, y lo que se pide es hallar las circunferencias tangentes a ambas rectas y a la circunferencia. Hay dos juegos de circunferencias solución. El primer caso supone dos circunferencias externas a la circunferencia inicial, y en el segundo caso las circunferencias contienen a la circunferencia inicial. Lo habitual es que solo te pidan un par de ellos, ya que hallar las cuatro circunferencias supone mucho tiempo y una gran cantidad de líneas que vuelve el ejercicio bastante confuso. Para simplificarlo, yo lo he dividido en dos ejercicios distintos, en uno hallarás las circunferencias externas, y en otro las internas.
Aunque no te lo creas, este ejercicio se resuelve igual que el ejercicio con dos rectas y un único punto. Para que lo veas, aquí tienes una aplicación interactiva, mueve el punto azul y lo comprobarás.
Aquí debajo tienes un vídeo con todo el proceso explicado, y un poco más abajo la transcripción y las láminas para poder realizar el ejercicio.
Resolución del primer par de circunferencias tangentes (externas)
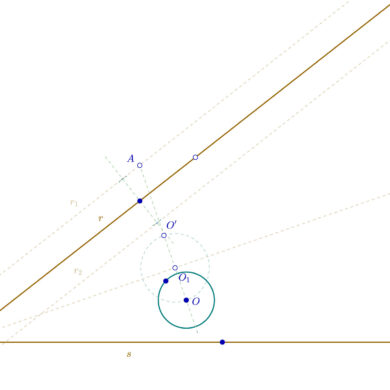
Tu punto de partida será algo similar a esto:
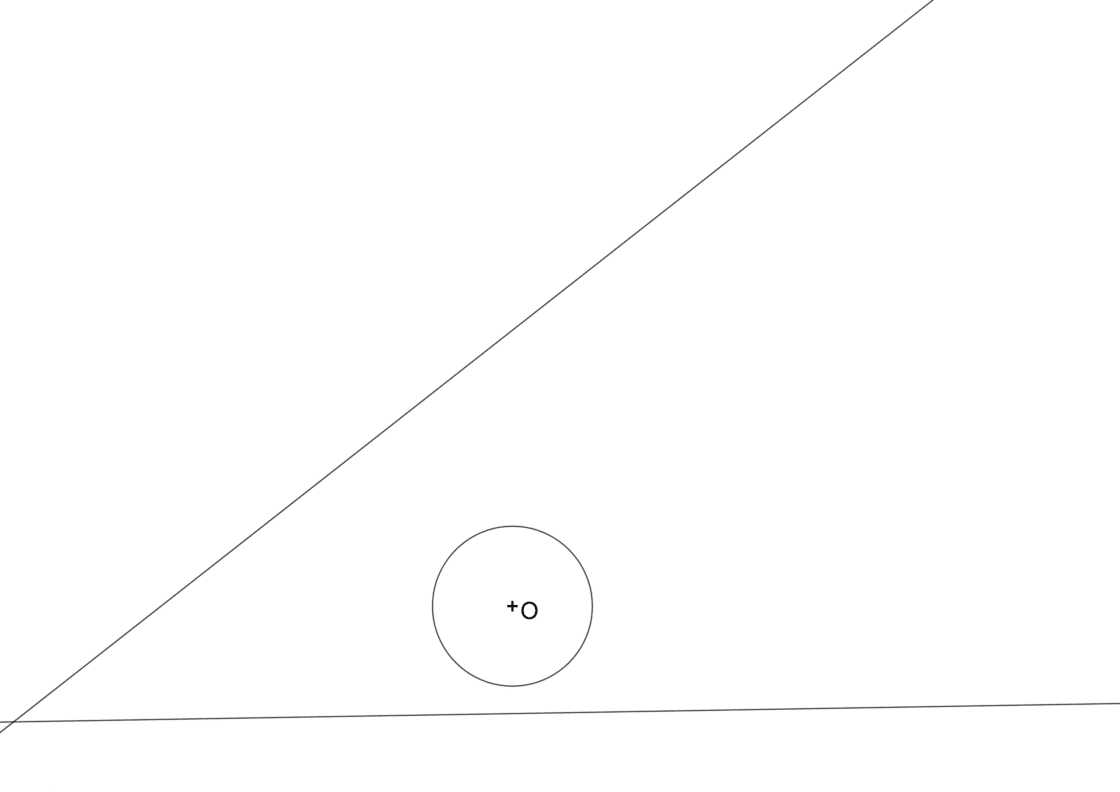
Trazamos por la recta más alejada de la circunferencia (en éste caso r) una recta paralela a la que llamaremos r1, separada de r por una distancia igual al radio de la circunferencia dada, y en la parte exterior de la recta. Si en vez de trazar la paralela por la recta más alejada de la circunferencia optamos por elegir la que esté más cerca, nos encontraremos con problemas más tarde, por lo que es importante tener en cuenta este punto.
Acto seguido hallaremos el punto O’ simétrico de O respecto a la bisectriz del ángulo que forman las dos rectas. La prolongación de la recta que forman O y O’ cortará a la paralela de r en el punto A.
Trazamos una circunferencia auxiliar con centro en el punto medio entre O y O’ (al que llamaremos O1) y con radio igual a la mitad de OO’
Desde A trazamos rectas tangentes a la circunferencia de centro O1, obteniendo los puntos de tangencia T1 y T2.
Ahora trazaremos un arco con centro en A y radio AT1, hallando los puntos de corte con la recta r1, que llamaremos C y D.
Trazamos perpendiculares a la recta r1 que pasan por los puntos C y D, donde estas rectas cortan a la bisectriz tendremos los puntos O2 y O3, solución de las dos circunferencias tangentes exteriores a la circunferencia dada.
Resolución del segundo par de circunferencias tangentes (que contienen a la inicial)
Tu punto de partida será algo similar a esto:
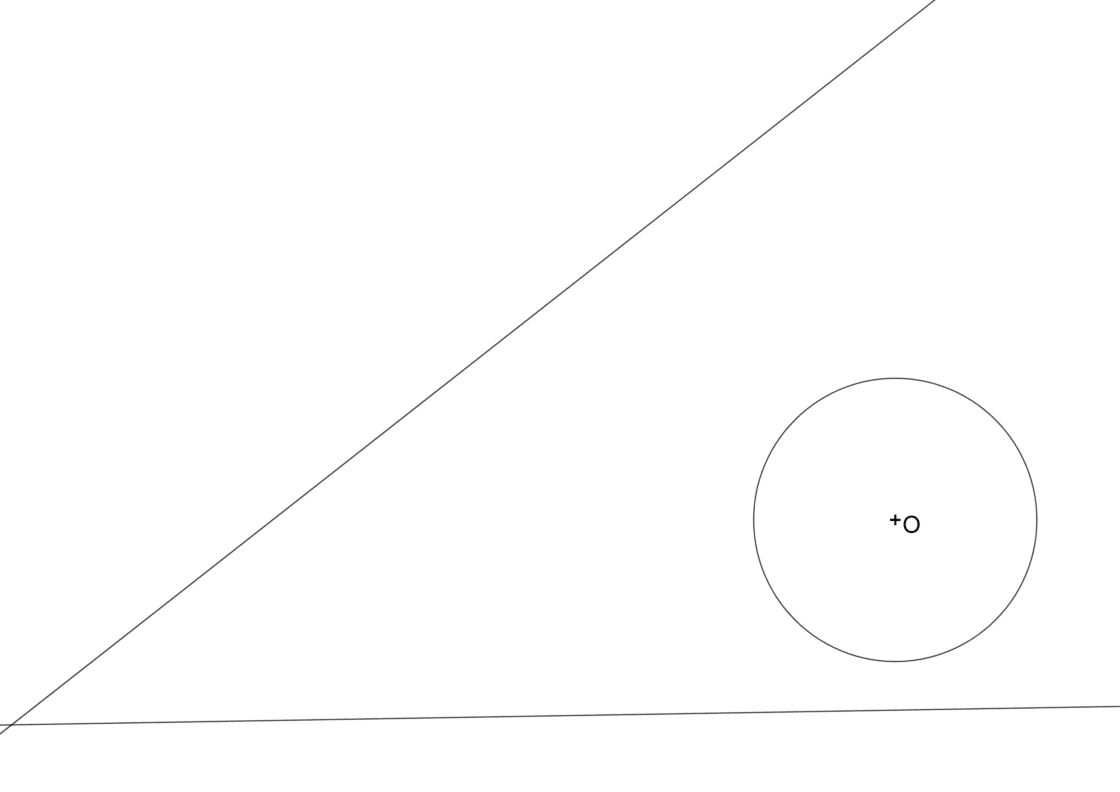
Al igual que en el acaso anterior trazamos por la recta más alejada de la circunferencia (en éste caso r) una recta paralela a la que llamaremos r2, separada de r por una distancia igual al radio de la circunferencia dada, y en la parte exterior de la recta. La diferencia es que en este caso la recta paralela la realizaremos hacia el interior, acercándonos a la circunferencia inicial.
Ahora dibuja el punto O’ simétrico de O respecto a la bisectriz del ángulo que forman las dos rectas. La prolongación de la recta que forman O y O’ cortará a la paralela de r en el punto B.
A continuación halla los puntos de tangencia de las rectas tangentes a la circunferencia auxiliar que pasan por el punto B. De éste modo obtienes los puntos de tangencia T3 y T4.
Con centro en B y radio BT3 trazamos un arco de circunferencia que corta a la recta r2 en E y F. Si trazamos perpendiculares a r2 que pasen por E y F hallaremos los centros de las circunferencias buscadas O3 y O4 en los puntos de corte con la bisectriz de las rectas.
Resolución final
Y en la siguiente imagen tenéis la resolución final con las cuatro circunferencias tangentes. Vale, a simple vista puede resultar un poco agobiante. Pero para facilitar las cosas te recomiendo que lo veas a pantalla completa en el ordenador y que hagas zoom sobre las partes de la construcción que quieras revisar.
Circunferencias tangentes a otra de centro conocido y que pasen por dos puntos dados.
En ésta ocasión se nos proporciona una circunferencia concreta con centro en O1 y dos puntos, P y Q por los que pasan ambas circunferencias. Hay que aclarar que las circunferencias que se buscan en este problema han de pasar de manera obligatoria por ambos puntos, P y Q. Si solo pasaran por uno de ellos cada una, habría infinitas soluciones.
Tu punto de partida será algo similar a esto:
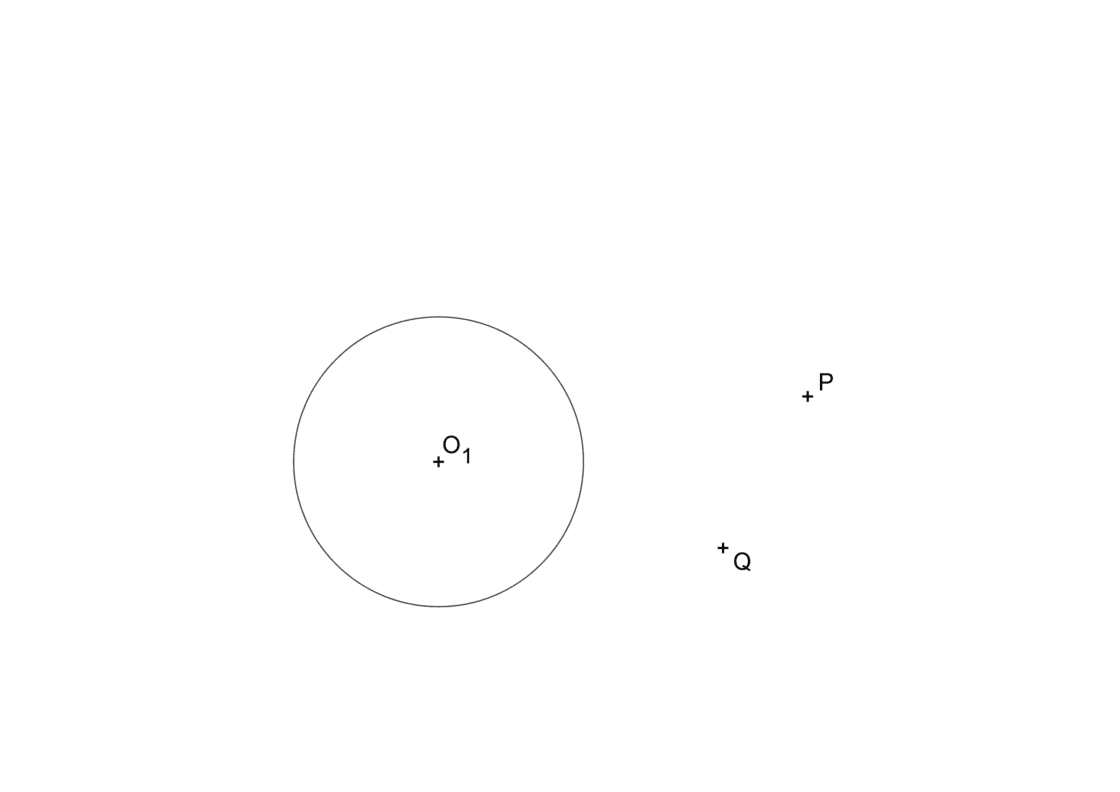
Aquí abajo tienes un vídeo con todo el proceso explicado paso a paso, y a continuación la transcripción de todo el ejercicio.
- El primer paso será unir P y Q y dibujar la mediatríz. Date cuenta de que sobre esa mediatríz se encontrarán los centros de ambas circunferencias. ¿Por qué lo se? Porque si tu dibujas la mediatríz de cualquier arco de cualquier circunferencia, siempre pasará por el centro de la misma.
- Ahora tienes que dibujar una circunferencia con centro en cualquier parte de esa mediatríz, pero es importante que el radio sea hasta P y que corte a la circunferencia que te dan.
- Los puntos donde esa circunferencia corta a la original los unes y prolongas la línea. Donde corta a la prolongación del segmento PQ tendrás el centro radical de las circunferencias.
- Tu siguiente paso será hallar los puntos de tangencia de la circunferencia inicial (de centro O1) con el centro radical Cr. Esos puntos serán T1 y T2
- Si unes O1 con T2 y prolongas la línea, el punto donde corten a la mediatríz de PQ será el centro O3 de una de las dos soluciones.
- Con centro en O3 y radio hasta T2 ya puedes dibujar la primera solución.
- Para hallar la segunda, une O1 con T1 y prolonga esa línea hasta que corte la mediatríz. Ese punto será O2 el otro centro que buscas.
- Pincha en O2 con el compás y mide de radio hasta T1 y de esa manera podrás dibujar la otra circunferencia y así habrás solucionado el problema.
Te puede interesar…
Potencia, eje radical y centro radical
Problema de Apolonio – Circunferencias tangentes a tres circunferencias
Circunferencias tangentes – Resolución de tangencias usando potencias
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
