Resolución de triángulos

En ésta sección os mostraré la resolución de triángulos sencillos. Siempre partiendo de la base de que conocemos algunos de sus elementos notables, como pueden ser lados, altura, base, etc. Este tipo de ejercicios están recomendados para el nivel de primero de bachillerato.

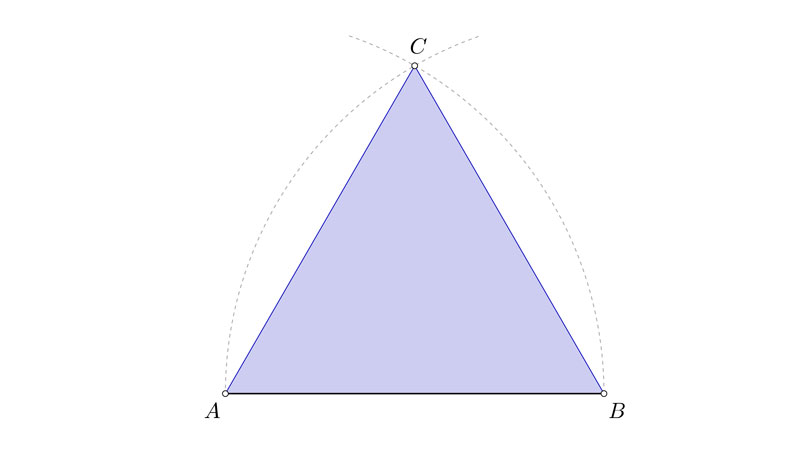
Construir un triángulo equilátero conocido el lado

Conocido el lado AB, se nos pide construir un triángulo equilátero. El ejercicio en si es muy sencillo de solucionar. Para ello solo tenemos que trazar dos arcos idénticos. Uno con centro en A, y radio AB y otro con centro en B y radio BA. El punto donde se corten nos indicará el vértice C que nos falta para la resolución del tríangulo equilátero de lado AB. Tu punto de partida será algo parecido a esto.

Aquí tienes un video donde puedes ver todo el proceso paso a paso.

Resolución de triángulos equiláteros conocida la altura

La resolución de triángulos equilateros conocida la altura es un proceso un poco más complejo que el anterior, pero no mucho. Para practicar considera una altura de 8cm, el principio será parecido a esto.

• En primer lugar, dibujamos una recta auxiliar r sobre la que dibujaremos la base más adelante.
• Dibujamos una perpendicular a la recta r por un punto cualquiera. Sobre esa perpendicular dibujaremos la altura h, hallando el punto C.
• Dividimos la altura h en tres partes iguales. Supongo que te acuerdas del Teorema de Thales.
• Partiendo desde el punto C contamos dos partes. Ese punto será el centro O de la circunferencia circunscrita al triángulo equilátero.
• Con centro en el centro O y radio OC, dibujamos una circunferencia que corta en A y B, los otros vértices del triángulo equilatero que buscamos.

Resolución de triángulos isósceles conociendo la altura y la base

Puedes dibujar un triángulo cuya base mide 10cm y su altura 7cm para practicar, de modo que tu punto de partida será parecido a esto. Para la resolución de triángulos isósceles cuando conocemos la altura y la base debemos realizar los siguientes pasos:

• En primer lugar dibujamos la base, el segmento AB, a partir del cual dibujaremos el triángulo.
• El siguiente paso es dibujar la mediatriz de la base, porque sobre ella se encuentra la altura.
• Sobre esa medriatriz que acabamos de dibujar llevamos la medida de la altura. De ese modo encontramos el punto C, que es el vértice que nos falta por conocer.
• Uniendo A, B y C podemos dibujar el triángulo isósceles de altura h y base AB que se nos pide.

Dibujar un triángulo isósceles conocidos los lados iguales y la altura

En ésta ocasión nos encontramos ante un problema de resolución de triángulos isósceles cuando lo que conocemos son los dos lados iguales y la altura desde la base. Puedes practicar dibujando un triángulo isósceles cuya altura mida 6cm y los lados iguales 7cm. Para solucionarlo debes hacer lo siguiente:

• Dibujamos una recta auxiliar r
• Por un punto cualquiera trazamos una perpendicular
• Partiendo desde la base, medimos la altura h, obteniendo el punto C
• Con centro en C, usando el compás, trazamos dos arcos de tamaño igual a los lados conocidos, cortando a la recta r en los puntos A y B
• Si unimos A, B y C, obtenemos el triángulo isósceles que buscamos.

Resolución de triángulos isósceles conocidos los ángulos iguales y la base

En ésta ocasión se nos pide la resolución de un triángulo isósceles conociendo los dos ángulos iguales y la base. Para poder resolverlo debemos recordar como trasladar ángulos. Para practicar este ejercicio, dibuja un triángulo cuya base sea de 10cm y los ángulos iguales de 45º.

• En primer lugar, dibujaremos una recta auxiliar r, y sobre ella llevaremos el segmento AB, que corresponde a la base.
• Con vértice en A, dibujaremos el ángulo que conocemos.

Llegados a éste punto, tenemos dos posibles maneras de resolver éste ejercicio.

1. Dibujar el mismo ángulo, pero con vértice en B y ver donde cortan.
2. Trazar la mediatriz del lado AB y ver donde corta la prolongación del ángulo.

Cualquiera de las dos opciones es válida.

Construir un triángulo isósceles conociendo la altura y el ángulo opuesto a la base

La resolución de triángulos isósceles cuando se nos dicen la base y el ángulo opuesto hace necesario conocer el proceso para dibujar la mediatriz de un segmento, dibujar paralelas, trasladar ángulos y hallar bisectrices. Para este ejercicio, puedes probar a dibujar un triángulo cuya altura sea de 7cm y el ángulo opuesto a la base de 60º.

• Para empezar, dibujaremos una recta r sobre la que situaremos la base, representada por el segmento AB.
• Acto seguido hallaremos la mediatriz del segmento AB.
• Por otra parte, debemos hallar la bisectriz del ángulo α
• Trasladamos la bisectriz del ángulo α sobre un punto cualquiera de la mediatriz de AB. Lo vamos a trasladar a ambos lados de la mediatriz, ya que lo que queremos es trasladar el ángulo entero, en realidad.
• Tanto por el punto A, como por el punto B, dibujamos paralelas a los lados del ángulo que acabamos de dibujar.
• El punto C de corte nos determina el vértice del triángulo que nos falta para resolver el ejercicio.

Resolución de triángulos rectángulos conociendo un cateto y la hipotenusa

Otro tipo de problemas de resolución de triángulos a los que nos podemos enfrentar es el siguiente. Conocemos uno de los catetos y la hipotenusa, pero desconocemos el otro cateto. Para este ejercicio vamos a suponer que la hipotenusa mide 10cm y que uno de los catetos mide 6cm… ¿Cuánto medirá el otro cateto?

• Dibujamos una recta auxiliar cualquiera r
• Por un punto cualquiera de esa recta, levantamos una perpendicular.
• Sobre esa perpendicular, llevamos la medida del cateto AC que conocemos.
• Desde el punto C, trazamos un arco que mide lo mismo que la hipotenusa, cuya medida si conocemos.
• El punto de corte con la recta r indica el punto B. De esa manera podemos hallar el cateto AB que desconocemos y terminar de dibujar el triángulo.

Construir un triángulo rectángulo conociendo un cateto y el ángulo opuesto

La resolución de triángulos rectángulos cuando conocemos un cateto AB y su ángulo opuesto α no es tan dificil como puede parecer. Te voy a enseñar como resolverlo de manera fácil y rápida. Para practicar realiza un triángulo con un cateto de 6cm y el ángulo opuesto de 30º

• En primer lugar, dibujamos una recta auxiliar r y sobre ella marcamos el cateto que conocemos AB
• Por el extremo A dibujaremos a continuación una perpendicular al cateto.
• Por un punto cualquiera de esa perpendicular trazamos el ángulo α que conocemos.
• Para terminar, realizamos una paralela al lado del ángulo que acabamos de dibujar, pero que pasa por B
• El punto de intersección de esa paralela con la perpendicular determina el punto C, que necesitamos para terminar el ejercicio.

Resolución de triángulos rectángulos cuando conocemos un cateto y su ángulo adyacente no recto

Siguiendo con los triángulos rectángulos, otro tipo de problema al que nos podemos enfrentar es la resolución de triángulos rectángulos cuando conocemos un cateto y su ángulo adyacente. Obviamente, debe ser el ángulo no recto, pues de lo contrario no podriamos resolverlo. Para practicar, dibuja un triángulo rectángulo sabiendo que un cateto mide 10cm y que su ángulo adyacente no recto mide 30º.

• Empezamos dibujando una recta auxiliar r, y sobre ella llevamos el cateto AB que conocemos.
• Por el extremo A vamos a levantar una perpendicular al segmento AB.
• Ahora por el extremo B llevaremos el ángulo adyacente α que si conocemos.
• El punto C de corte entre la perpendicular y el lado del ángulo α es el punto que necesitamos para resolver el ejercicio.

Dibujar un triángulo escaleno cuando conocemos sus tres lados

En el caso de los triángulos escalenos, el problema más básico sería el de la resolución de triángulos cuando conocemos sus tres lados. El proceso es muy sencillo, para practicar, dibuja un triángulo escaleno cuyos lados miden 10cm, 9cm y 6cm respectivamente.

• Vamos a dibujar una recta auxiliar r, y sobre ella llevaremos uno de los lados. Por comodidad, recomiendo elegir el más largo de los tres, que será la hipotenusa. Los extremos los llamaremos A y B.
• Por el punto A, utilizando el compás, vamos a dibujar un arco que mida lo mismo que el lado b,
• Acto seguido, por el punto B, vamos a dibujar con el compás otro arco, pero en ésta ocasión debe medir lo mismo que el lado a.
• El punto de corte de ambos arcos nos indica el punto C, que será el vértice que nos ayudará a terminar de dibujar el triángulo.