Tipos de transformaciones geométricas, isométricas, isomórficas y anamórficas: Giro, traslación, simetría.

Cuando hablamos de tipos de transformaciones geométricas podemos encontrar dos grandes grupos; las transformaciones isomórficas y las transformaciones anamórficas. Éstas a su vez se pueden dividir en otros tipos distintos. Pero antes de empezar, déjame recordarte de lo que estamos hablando

Éste tipo de operaciones lo que nos permiten es dibujar una figura igual, semejante o distinta, a partir de una forma inicial. Por eso éste tema está muy relacionado con el que explica como dibujar figuras iguales o trazar formas semejantes o a escala.

La nueva forma dibujada se dice que es homóloga de la forma original. Por otra parte, una transformación implica una correspondencia entre dos elementos que forman parte de un conjunto. Precisamente un buen ejemplo es cualquier figura, ya que es un conjunto de puntos.

Diferentes tipos de transformaciones geométricas

Si nos referimos a la dirección de la figura, podemos encontrar dos tipos de transformaciones geométricas distintas, las directas y las inversas.

• En las transformaciones directas la figura resultante u homóloga mantiene la misma dirección de la figura original en el plano.
• Por otra parte, en las transformaciones inversas la forma original y su homóloga tienen sentidos opuestos.

Dependiendo de la relación que mantienen la forma original y la homóloga se pueden clasificar en:

Transformaciones isométricas

Las transformaciones isométricas son un tipo de transformaciones geométricas en las cuales la forma homologa mantiene la misma apariencia que la figura original. Es decir, son procedimientos mediante los cuales construimos figuras que mantienen los mismos ángulos, y sus dimensiones también son iguales, tanto en longitud como en área. También se les suele denominar movimientos. Podemos encontrar las siguientes:

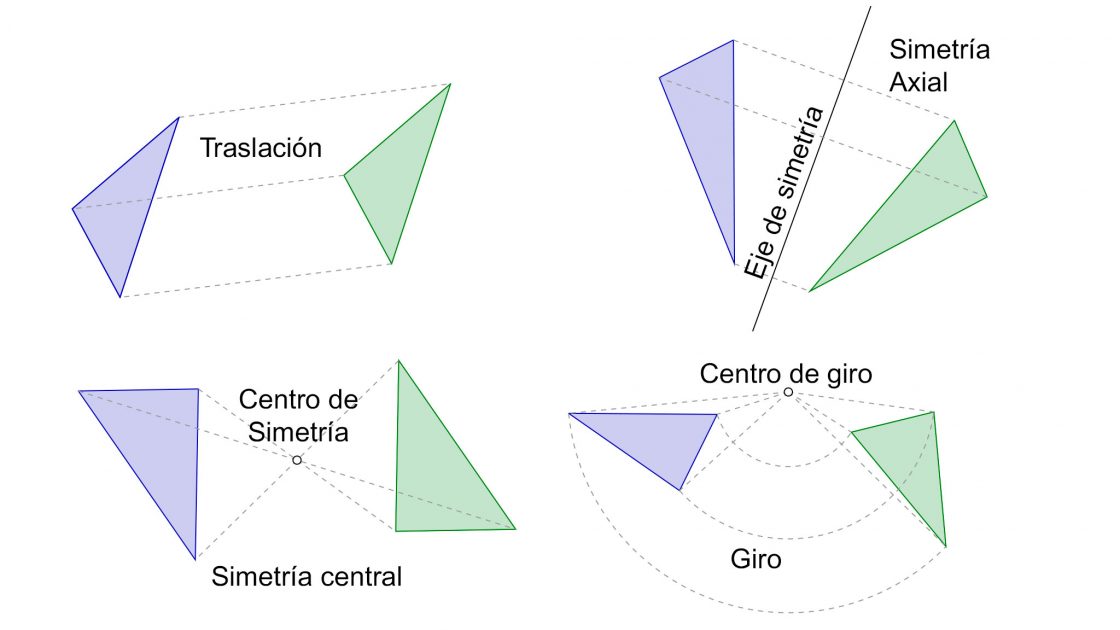
Traslación de figuras

Usando éste método, puedes dibujar figuras que tienen todos sus lados iguales de forma rápida y fácil. Por lo general en éste tipo de ejercicios te indican la dirección en que se debe desplazar la figura con una flecha, y te dicen a que distancia se debe mover. Aquí tienes una lámina para practicar. Si la imprimes en A4 debes moverla 15cm, y si la imprimes en un A6 (una cuartilla) debes moverla 7cm. Tu punto de partida será algo semejante a esto:

• El procedimiento es realmente sencillo. Todo lo que tienes que hacer es dibujar líneas paralelas a la dirección dada por cada uno de los puntos.
• Una vez tienes las líneas paralelas, sobre ellas debes medir la distancia que te indican desde cada punto. De esa manera tendrás los puntos A’, B’, C’, D’ y E’.
• Uniendo los puntos A’, B’, C’, D’ y E’ tendrás la figura homóloga trasladada.

Giro

Todos los puntos de la figura giran el mismo ángulo alrededor de un punto fijo que se denomina centro de giro. El sentido de giro puede ser tanto negativo como positivo. Lo más habitual es que te pidan girar un polígono o figura, proporcionándote el centro de giro y el ángulo a girar. Puedes practicar con la siguiente lámina. En este caso, se pide girar la figura alrededor del centro O 105º. Tu punto de partida será algo similar a lo siguiente:

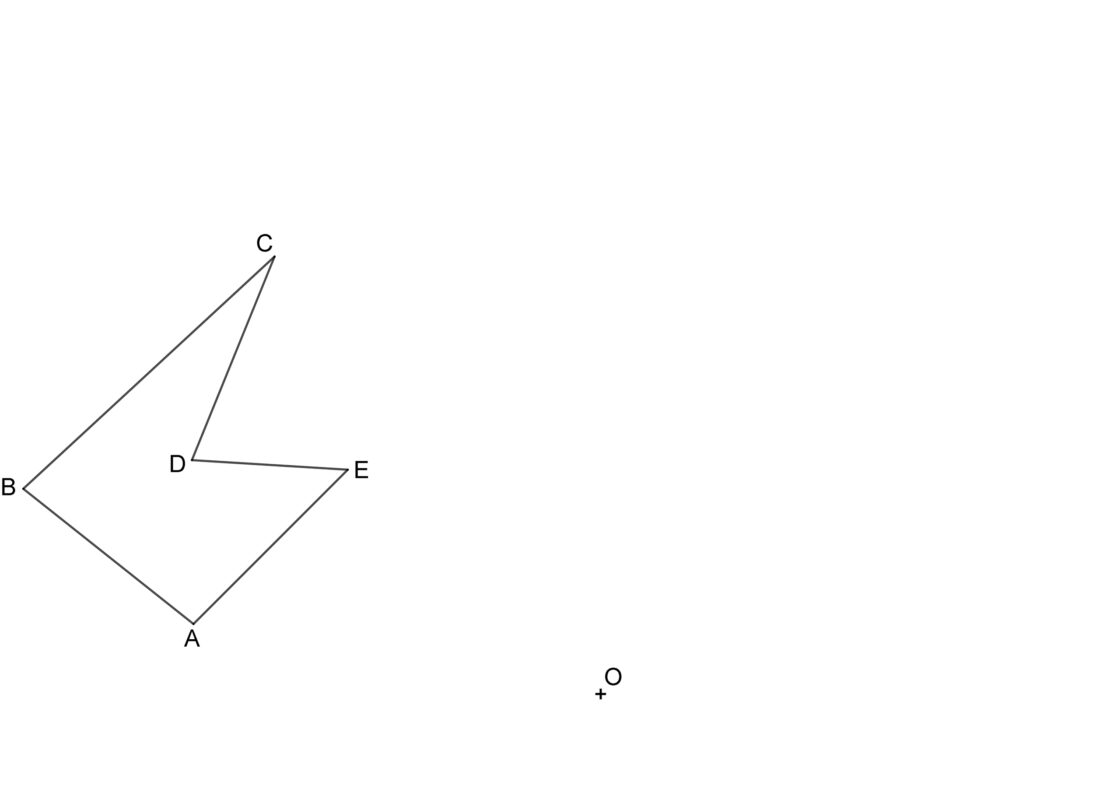
1. Empieza marcando la línea que une A con O.
2. Utilizando esa línea como referencia, marca el ángulo que te indican. En este ejemplo el ángulo utilizado es de 135 grados.
3. Usa el compás para realizar un arco que tenga por centro O y por radio hasta A. Donde ese arco corta al ángulo que marcaste antes tienes el punto A’.
4. Dibuja un arco con centro en O y radio hasta B.
5. Mide con el compás la distancia entre A y B, y luego mide esa misma distancia desde A’. El punto donde corta al arco que pasa por B es B’.
6. Repite ese paso con los demás puntos para hallar C’, D’ y E’.
7. Uniendo todos esos puntos tienes la figura original girada el ángulo que te proporcionan.

Si no te aclaras con el método anterior, siempre puedes dibujar la recta que une O con cada uno de los puntos A, B, C, D, E… Y medir el ángulo cada vez, de modo que OA’ forme un ángulo de 135º (o el que sea) con el segmento AO. Y así todos los demás; BO formará un ángulo de 135º con OB’… CO formará un ángulo de 135º con OC’… y así sucesivalente.

Aquí abajo puedes mover los puntos de la figura original. También puedes mover el punto A’ para modificar el ángulo y comprobar que la figura resultante es igual que la figura original.

Espero que este arcoíris tan bonito te aclare las ideas… ???

Simetría axial

Los puntos de la figura homóloga y de la original se encuentran a la misma distancia de un eje, tomando las medidas en perpendicular. En la naturaleza se da muy a menudo, tanto en seres vivos como en minerales. Un ejemplo muy evidente es el de las mariposas, donde el cuerpo hace de eje de simetría.

No obstante quiero hacer una aclaración. La simetría axial es una transformación isométrica, ya que la figura resultante mide lo mismo y tiene los mismos ángulos y área. Pero la figura no es igual, por eso es también una transformación anamórfica.

Puedes utilizar la siguiente lámina para practicar este ejercicio.

1. Traza perpendiculares al eje de simetría por cada uno de los puntos; A, B, C, D, E…
2. Los puntos donde esas perpendiculares cortan al eje llámalos P, R, S, T, V…
3. Con el compás, mide tomando como centro esos puntos, y como radio hasta el punto que les corresponde. En este ejemplo al punto R le corresponde A. Al punto S le corresponde B y así sucesivamente.
4. Luego, con esa misma medida, marca en el otro extremo de la línea el punto simétrico a cada uno de los originales. Por ejemplo, para A medirás de R a A, y giras el compás (sin levantarlo del papel) para ver donde corta a la línea perpendicular que pasa por A en el otro lado del eje. Ese punto es A’.
5. Para terminar solo tienes que repetir el proceso con los demás puntos.

Aquí abajo puedes mover los puntos de la figura original para modificar su forma, y el punto P para modificar la posición del eje.

Simetría central

Similar a la anterior, solo que los puntos equidistan de un punto que se denomina centro de simetría. La figura homóloga se encuentra girada 180 grados respecto de la original. Puedes practicar con la lámina siguiente:

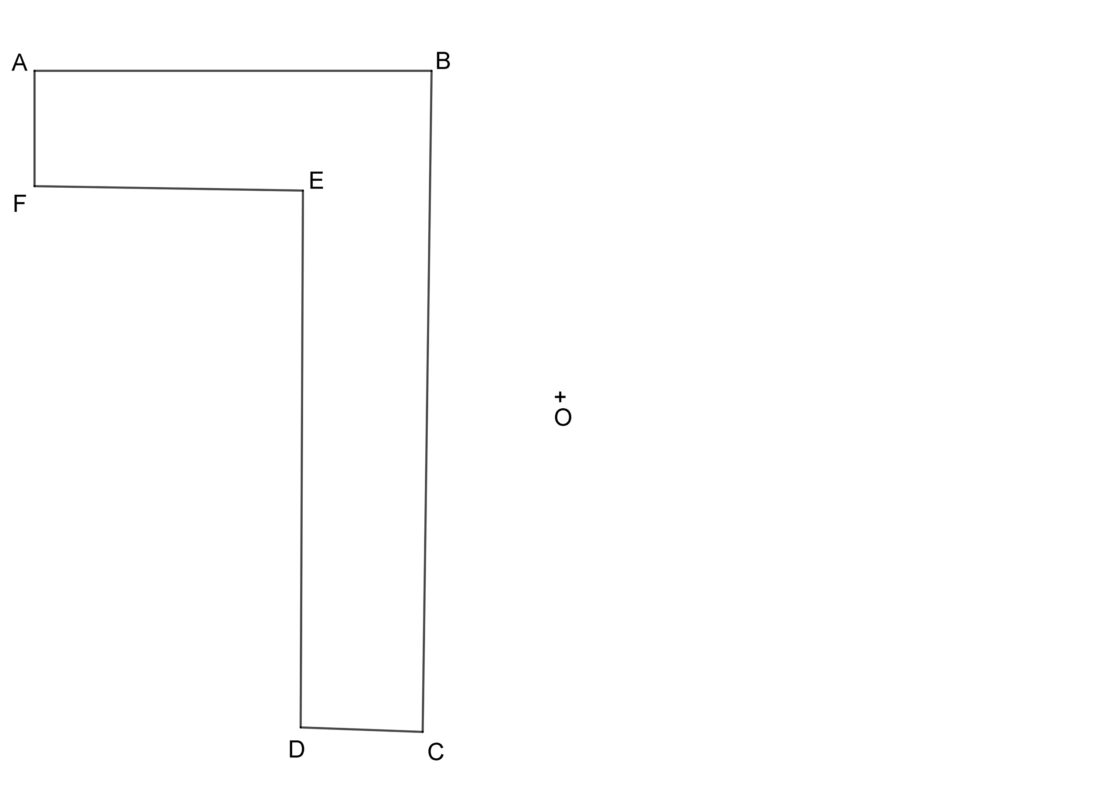
1. Empieza por dibujar líneas que pasen por cada uno de los puntos y por el centro O de simetría.
2. Pincha con el compás en O y abre hasta A. Sin levantar la punta de O mueve el compás para ver donde corta a la línea que pasa por O y A. El punto donde corta es A’.
3. Luego, sin levantar el compás de O, mide la distancia entre O y B. Lleva esa misma distancia, sin levantar tampoco el compás, sobre la recta que pasa por O y B. Ese punto de corte es B’.
4. Repite la operación con todos los demás puntos para completar la figura.

Aquí abajo puedes mover tanto el centro O de simetría como los puntos de la figura original para ver como se comporta este tipo de simetría.

Transformaciones isomórficas

En las transformaciones isomórficas, la figura homóloga (la resultante) mantiene los ángulos y proporciones de la forma original. Entre la figura original y la homóloga existe una relación de proporcionalidad o escala. En éste tipo de transformaciones geométricas las figuras resultantes tienen la misma forma, pero por lo general no tienen el mismo tamaño. No obstante hay determinadas transformaciones isométricas que son también isomórficas, como el giro, la traslación y la simetría axial. Podemos encontrar los siguientes tipos de transformaciones isomórficas:

• Semejanza: Se dice que dos figuras son semejantes cuando tienen sus ángulos iguales y sus lados proporcionales. La razón de proporción viene definida por la razón de semejanza, que se representa con la letra K. De tal manera que una una figura a razón 2 significaría que los lados miden el doble en la figura homóloga que en la original. Si quieres más información sobre este tipo de transformación te recomiendo visitar la entrada donde hablo de los distintos tipos de procedimientos para dibujar figuras semejantes.
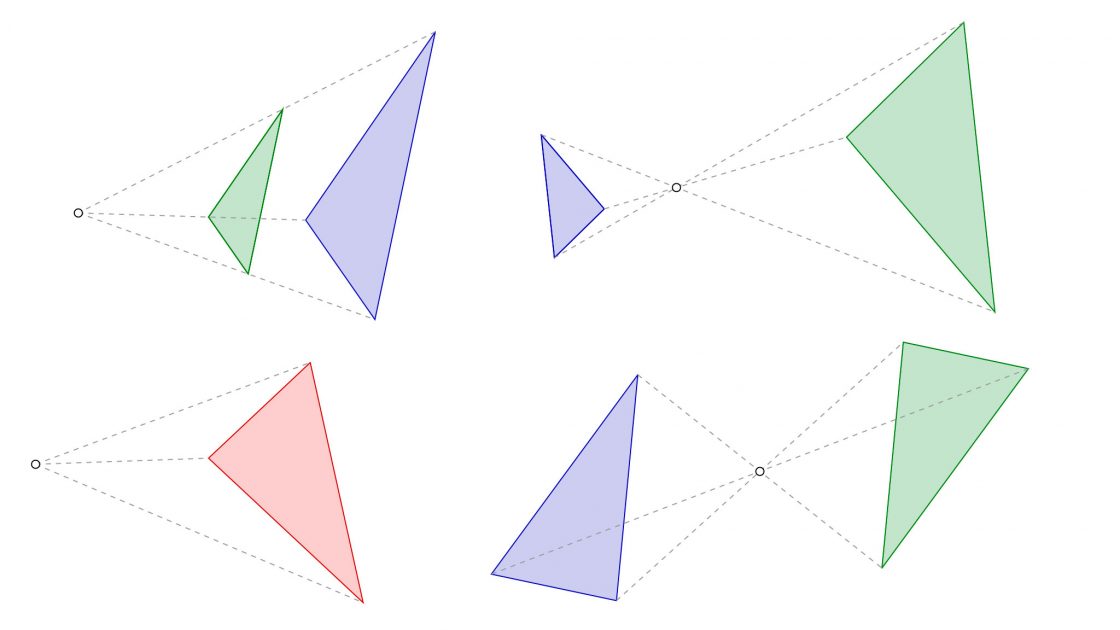
• Homotecia: Es una transformación geométrica en la que los puntos homólogos se encuentran alineados respecto a los originales tomando como referencia un punto que se denomina centro de homotecia. Si quieres saber más sobre esta transformación, te recomiendo echarle un ojo al artículo en el que hablo de la homotecia y sus diferentes tipos.

Transformaciones anamórficas

De entre los tipos de transformaciones geométricas que nos podemos encontrar, las transformaciones anamórficas suelen ser las más complicadas de todas. En este tipo de representaciones las figuras resultantes no mantienen ni la forma, ni los ángulos de la figura original. Por este motivo la figura homóloga es completamente distinta de la que se usa como modelo. Los tipos de transformaciones anamórficas que podemos encontrar son:

• Equivalencia: Las figuras equivalentes tienen la misma superficie, pero distinta forma.
• Inversión: Este tipo de transformación anamórfica implica que a cada punto de la figura original le corresponde un punto homólogo en el mismo plano y que está alineado respecto del original tomando como referencia un punto que se llama centro de inversión. Se da además la propiedad de que el producto de sus distancias respecto al centro de inversión es constante. Si quieres saber más de este tipo de transformaciones, puedes visitar la entrada donde explico la inversión en geometría.

Ayúdame a mejorar esta entrada

¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti.

«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.