Semejanza. Construcción de figuras semejantes y proporcionales

Se dice que dos figuras son semejantes cuando tienen todos sus ángulos iguales, y los lados son proporcionales. La proporcionalidad existente entre dos lados homólogos se denomina razón de semejanza. Este tipo de construcciones son útiles a la hora de realizar maquetas, por ejemplo. Está muy relacionado con el concepto de escala, que se utiliza continuamente en ingeniería y construcción.

Por ejemplo, al referirnos a triángulos, se dice que dos triángulos son semejantes cuando:

Sus tres ángulos son iguales α=α’ β=β’ γ=γ’.
Si decimos que k es la razón de proporción, entonces sus tres lados son proporcionales de la siguiente manera: a/a’=b/b=c/c’=k
Dos de sus lados proporcionales y el ángulo entre ellos igual. En este caso, por defecto, los otros dos ángulos serán iguales y los lados también proporcionales.

En el caso de las circunferencias, estas siempre son semejantes. La razón de proporción entre ellas será la proporción existente entre sus radios o diámetros.

Dos formas poligonales (regulares o irregulares) serán semejantes si se cumplen las mismas condiciones que para los triángulos. Ten en cuenta que cualquier polígono se puede dividir en triángulos. Por lo tanto, si los triángulos resultantes son semejantes, la forma poligonal también lo será.

Dibujar figuras semejantes usando perpendiculares

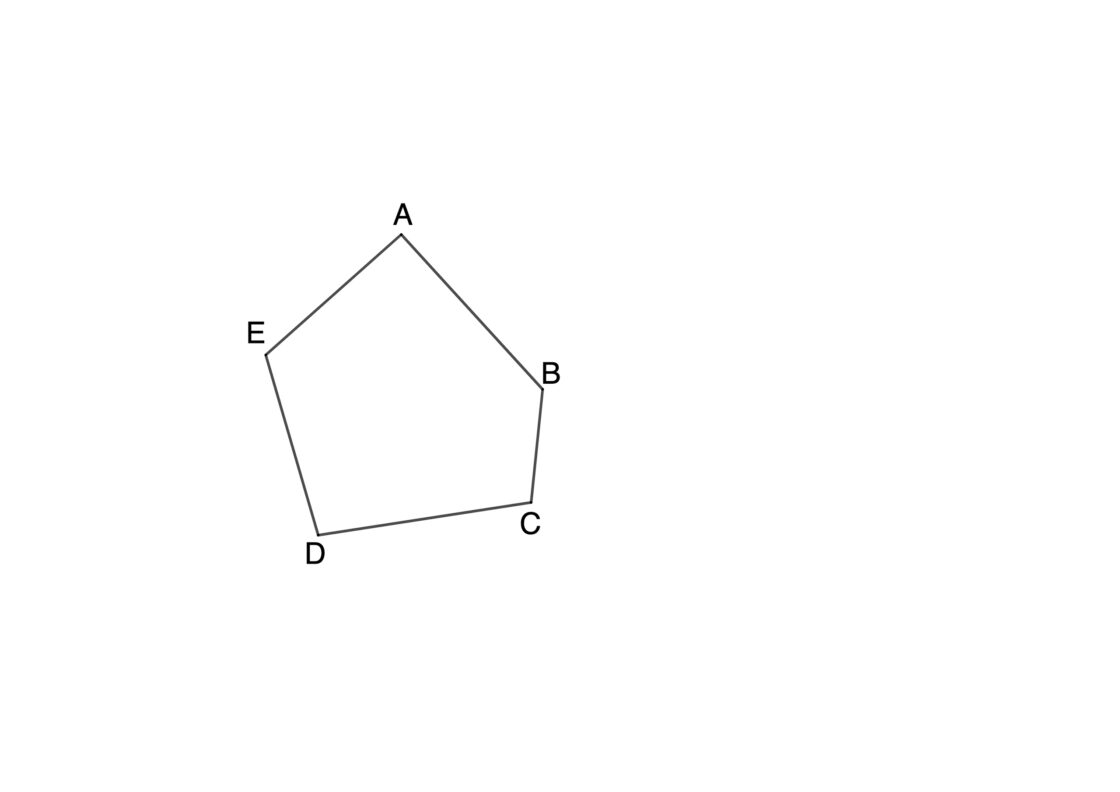
Para construir figuras semejantes usando perpendiculares es imprescindible conocer la razón de semejanza. En su defecto, si no se conoce la razón de semejanza, deberías conocer la longitud de un lado homólogo. Por ejemplo A’B’, para de esa manera, hallar tú la razón de semejanza y después construir la figura. Aquí tienes una plantilla para poder trabajar este ejercicio:

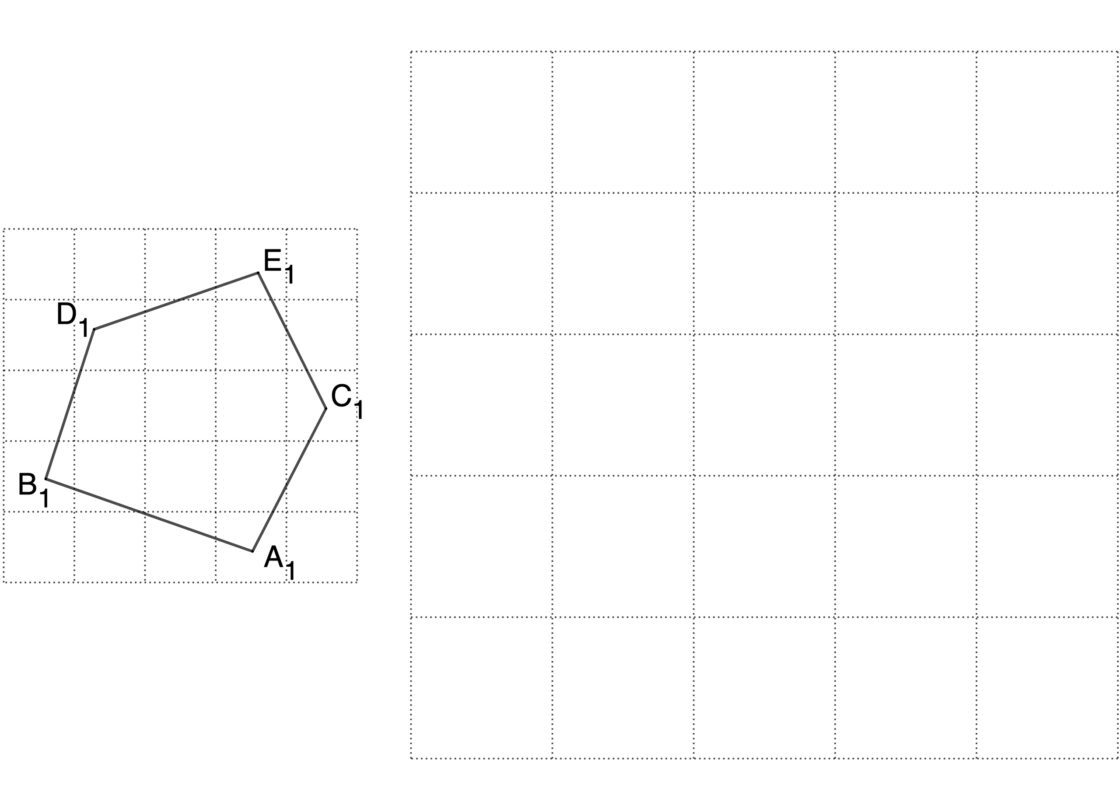
Traza una recta auxiliar y sobre ella traza perpendiculares por los vértices de la figura. De esa manera obtienes A₁, B₁, C₁, D₁ y E₁
Dibuja otra recta auxiliar donde vayas a construir la figura semejante y marca sobre ella el punto A₂ a partir del cual construirás la figura semejante.
Sobre esa línea, y a partir de A₂, lleva la medida hasta B₂, C₂… multiplicando esas medidas por la razón de semejanza.
Levanta perpendiculares por A₂, B₂, C₂… Sobre esas perpendiculares lleva la medida de A₁ a A, la de B₁ a B… y así sucesivamente, siempre multiplicando dichas medidas por la razón de semejanza.
Así obtienes los puntos A’, B’, C’… con los que acabas de dibujar la figura semejante.

Construcción de una figura semejante a otra por radiación

Este método es una aplicación de la homotecia en la construcción de figuras semejantes. Para que puedas practicar, puedes usar la siguiente lámina:

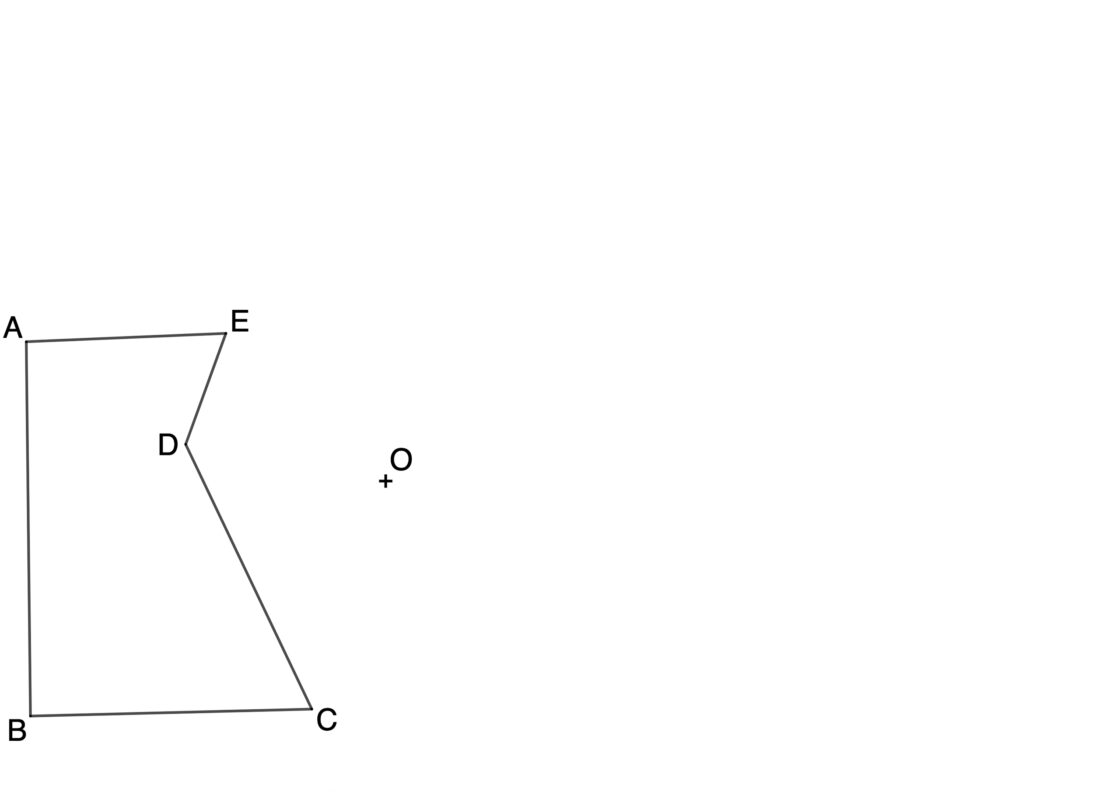
Dada una figura que se quiere replicar, se marca un punto O que utilizarás como referencia.
Dibuja líneas que pasen por O y por cada uno de los vértices de la figura inicial.
Usando el teorema de Tales divide cada uno de los segmentos OA, OB, etc. En tantas partes como necesites para hallar la razón de semejanza. Por ejemplo, si la razón de semejanza fueran 3/2 tendrías que dividirla entre dos y luego llevar uno. Para 5/4 dividirías entre 4 y te llevarías uno más. En este caso es fácil porque la razón es 2, solo tienes que duplicar las medidas.
Lleva las nuevas medidas sobre las rectas que dibujaste antes para hallar los puntos A’, B’, C’, etc.

Dibujar figuras semejantes mediante una cuadrícula

La forma de dibujar figuras semejantes utilizando una cuadrícula es la siguiente. Partimos de la base de que conocemos la figura inicial, y por supuesto la razón de proporción. Quiero aclarar que este método no es el más adecuado para dibujar formas poligonales. Seguro que ya has usado este método en el pasado, pero aplicado a otro tipo de dibujos más relacionados con el mundo del arte, como animales, personas, lugares o edificios, etc. De todas formas te dejo una lámina sencilla para entender el concepto. Para simplificar te dejo dibujada ya la cuadrícula final.

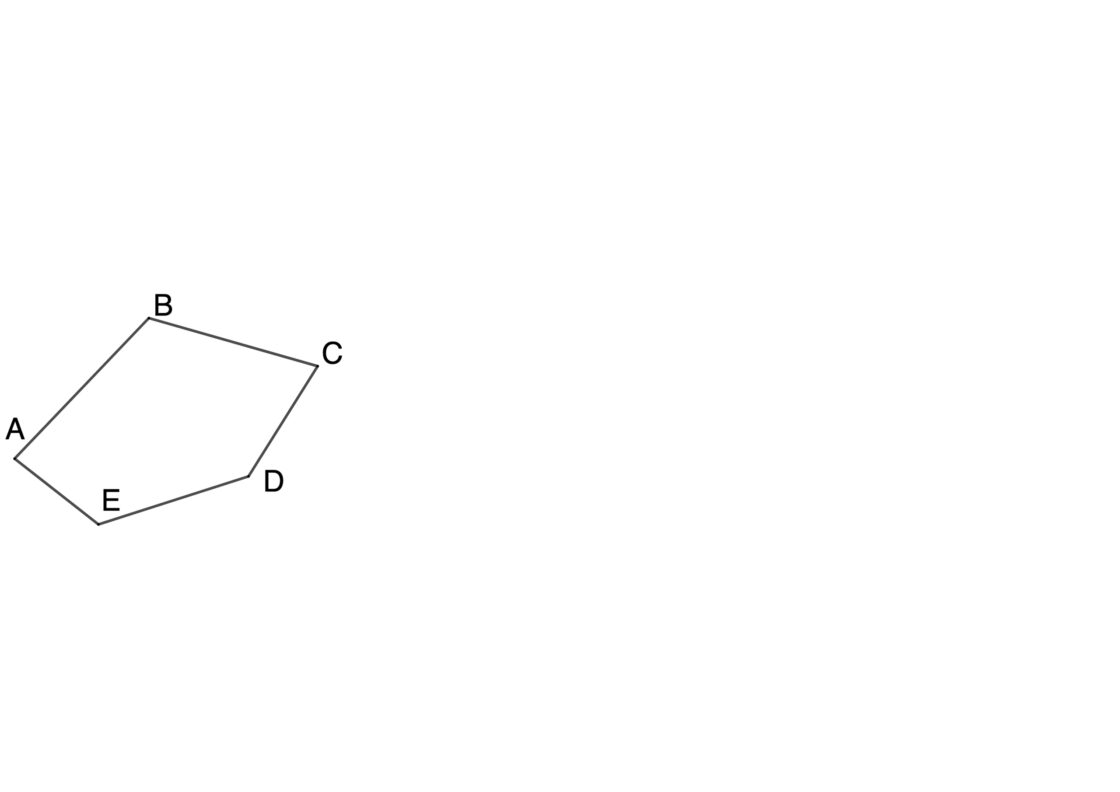
Lo primero que debes hacer es dibujar una cuadrícula de tal manera que los pequeños cuadrados resultantes tengan como lado la unidad de medida que sea (centímetros, milímetros, metros, etc.)
En el lugar donde quieres dibujar la figura proporcional dibujas otra cuadrícula, pero en esta ocasión los cuadrados pequeños deben tener de lado la unidad de medida multiplicada por la razón de proporción.
Una vez tienes la cuadrícula, solo tienes que medir distancias sobre la cuadrícula original y llevarlas sobre la nueva cuadrícula.

Construcción de una figura inversamente proporcional a otra

La forma más sencilla de resolver este ejercicio es aplicar el concepto de homotecia. Partimos de la base de una figura cualquiera (en este ejemplo usaré un triángulo de vértices ABC). También conoces la razón de proporción, que para este ejercicio vamos a considerar que es -1.5

Empieza por marcar un punto cualquiera que será el centro de homotecia. Llámalo O.
Dibuja líneas que pasen por cada uno de los vértices y por el centro de homotecia (el punto O).
Multiplica la distancia que hay desde cada uno de los puntos hasta O por el centro de homotecia. Luego traslada esa misma medida, cada una sobre su línea.
De esa manera hallas los puntos A’, B’ y C’ que forman la figura inversamente proporcional.

Si quieres practicar con algo un poco más complejo, puedes practicar dibujando una figura que sea inversamente proporcional a la que aparece en esta lámina aplicando razón 2.