La inversión es una transformación geométrica por la cual a cada punto A le corresponde un punto A’, cumpliendo las siguientes condiciones:
- Ambos puntos A y A’ se encuentran alineados respecto otro punto fijo O, llamado centro de inversión.
- El valor del producto de los segmentos OA y OA’ es una constante llamada potencia de inversión. Esta constante se suele identificar con la letra k.
La potencia de inversión será positiva cuando ambos puntos se encuentran al mismo lado respecto de O, y negativa cuando O se encuentra entre ellos. Ten en cuenta que si O representa la distancia cero, medida en una dirección sería positiva, mientras que en la otra sería negativa. Como ya sabes, un número positivo multiplicado por un punto negativo da como resultado un valor negativo.
En la siguiente aplicación interactiva puedes comprobarlo moviendo el centro de inversión O. Fíjate que si el punto está dentro de la circunferencia, entonces la potencia de inversión será negativa. Por otra parte, si está fuera, al estar ambos segmentos en el mismo respecto de O, entonces la potencia será positiva.
Si acabas de estudiar la resolución de tangencias usando el concepto de potencia, tal vez te estés preguntando que diferencia hay entre una cosa y la otra. Bien, para ser sinceros, ninguna en absoluto. La potencia es un caso particular de la inversión que solo se aplica a la circunferencia. ¡Ojo! Solo a la circunferencia, no a los puntos dentro de ella. Por otra parte, la inversión se refiere a cualquier punto del plano, incluyendo rectas y otro tipo de polígonos.
Elementos y figuras dobles en la inversión
Cuando hablamos de puntos dobles en una relación de inversión, nos referimos a aquellos que son inversos de si mismos. Para que esto se de, si la potencia es mayor de cero, la distancia al centro de inversión debe ser la raíz cuadrada de k. Si lo piensas un poco, significa que todos esos puntos se encuentran a una distancia constante del centro de inversión. Eso significa que dibujan una circunferencia de centro O y radio igual a la raíz cuadrada de k. Esta circunferencia recibe el nombre de circunferencia de puntos dobles o de autoinversión.
En la siguiente aplicación puedes mover el punto P y el punto P’ se calculará solo para mantener la potencia constante. Fíjate que la circunferencia azul es la circunferencia de puntos dobles. La forman todos los puntos que son dobles de si mismos.
Ten en cuenta que en la inversión negativa no existen puntos dobles, ya que los puntos siempre se encuentran en lados opuestos a O. Esto se puede explicar matemáticamente de una forma fácil. Como imagino que ya sabes, un valor negativo nunca puede ser el producto de dos valores positivos o negativos. Para que k<0 obligatoriamente un valor ha de ser positivo y otro negativo. Por lo tanto es imposible que estén en el mismo lugar.
Aunque la única figura que es doble punto a punto es la circunferencia de puntos dobles, existen otra serie de figuras o puntos que también lo son porque los puntos se corresponden con otros que pertenecen a la misma figura. Por ejemplo, las rectas que pasan por el centro de inversión se consideran dobles, aunque solo las que pasan por la circunferencia de autoinversión tienen el mismo valor.
También se consideran dobles aquellas circunferencias respecto a las cuales el centro de inversión tenga una potencia de inversión igual a k. Pueden darse dos casos, que la potencia sea positiva, o que la potencia sea negativa. Para ponerlo en palabras más sencillas. Son dobles las circunferencias cuyos centros son la intersección de dos rectas tangentes a la circunferencia de puntos dobles. En el siguiente ejemplo puedes comprobarlo moviendo los puntos azules.
Inversión circunferencia-recta
Una propiedad curiosa en la inversión es que la figura inversa de una circunferencia que pasa por el centro de inversión es una recta paralela a la recta tangente en la circunferencia por el centro de inversión. Dicho así resulta un poco complejo de entender, pero seguro que la aplicación de aquí abajo te aclara las ideas sobre este concepto. Como siempre, puedes mover los puntos azules para verificar que efectivamente se cumple.
Sobre este mismo tema, te propongo un juego si no te lo acabas de creer. En la siguiente aplicación puedes mover el centro de inversión. Mira lo que ocurre con la circunferencia azul cuando lo acercas a la circunferencia negra. También puedes mover los puntos A, B, C y A’ para verificar que la potencia de inversión permanece constante.
Te puede interesar…
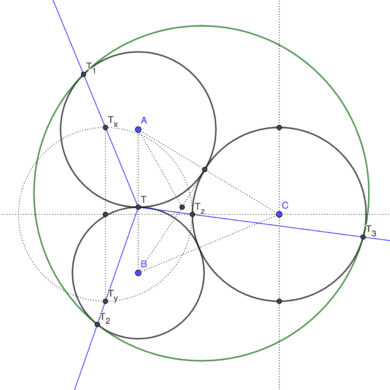
Circunferencia tangente a tres circunferencias tangentes
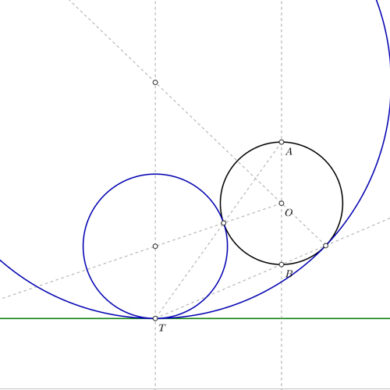
Resolución de circunferencias tangentes usando inversión
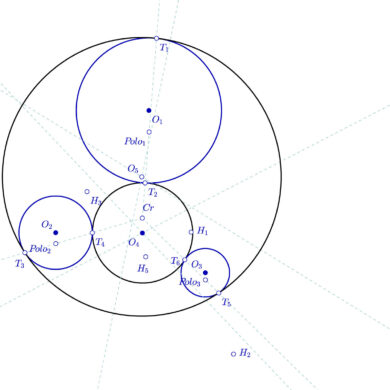
Problema de Apolonio – Circunferencias tangentes a tres circunferencias
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
