Las rectas tangentes a la elipse son desde mi punto de vista los ejercicios de tangencias a curvas cónicas más sencillos que hay. Además, una vez conozcas los procedimientos y elementos, te darás cuenta de que hallar las tangentes a cualquier otro tipo de curva cónica es prácticamente igual.
Recta tangente a una elipse por un punto de la misma
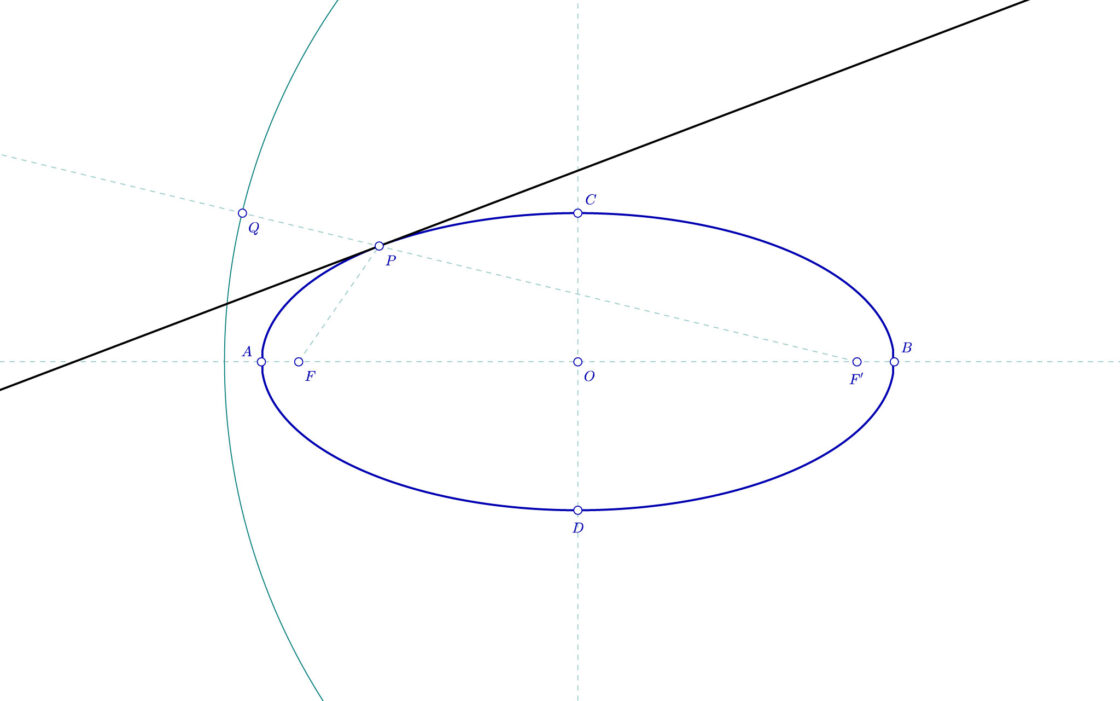
Se nos pide hallar las rectas tangentes a una elipse conocidos el eje mayor AB y el eje menor CD y que pasan por un punto T que pertenece a dicha elipse. Si no conocemos los focos, el primer paso será hallarlos. Si los conocemos, trazamos la circunferencia focal que corresponde al foco más alejado del punto. En éste caso F’.
Tu punto de partida será algo semejante a ésto:

Prolongamos la recta que parte de F’ y pasa por T hasta cortar a la circunferencia focal en el punto Q. Una vez conocido esto, si trazamos la bisectriz del ángulo FTQ, habremos hallado la tangente buscada. Tened en cuenta que en éste caso solo encontraremos una única recta al tratarse de un punto propio a la elipse.
Imagina que al tratar de dibujar la circunferencia focal te das cuenta de que el punto Q queda fuera del plano. Entonces tienes otra solución posible. Dibuja la bisectriz del ángulo que forman F, B y F’ y después dibuja la perpendicular a dicha recta por el punto T.
Aquí abajo tienes una aplicación interactiva de ambas soluciones para que puedas verificar el resultado.
Si todavía no te ha quedado claro, aquí abajo tienes un vídeo para ver como se resuelve este ejercicio.
Rectas que pasan por un punto exterior y son tangentes a la elipse
En éste caso se nos pide hallar las rectas que pasan por un punto externo a la elipse y que son tangentes a la misma. Como en el caso anterior, se nos proporcionan los dos ejes. Si no se nos indican los focos, deberemos hallarlos para poder continuar. Tu punto de partida debería parecerse a lo siguiente:
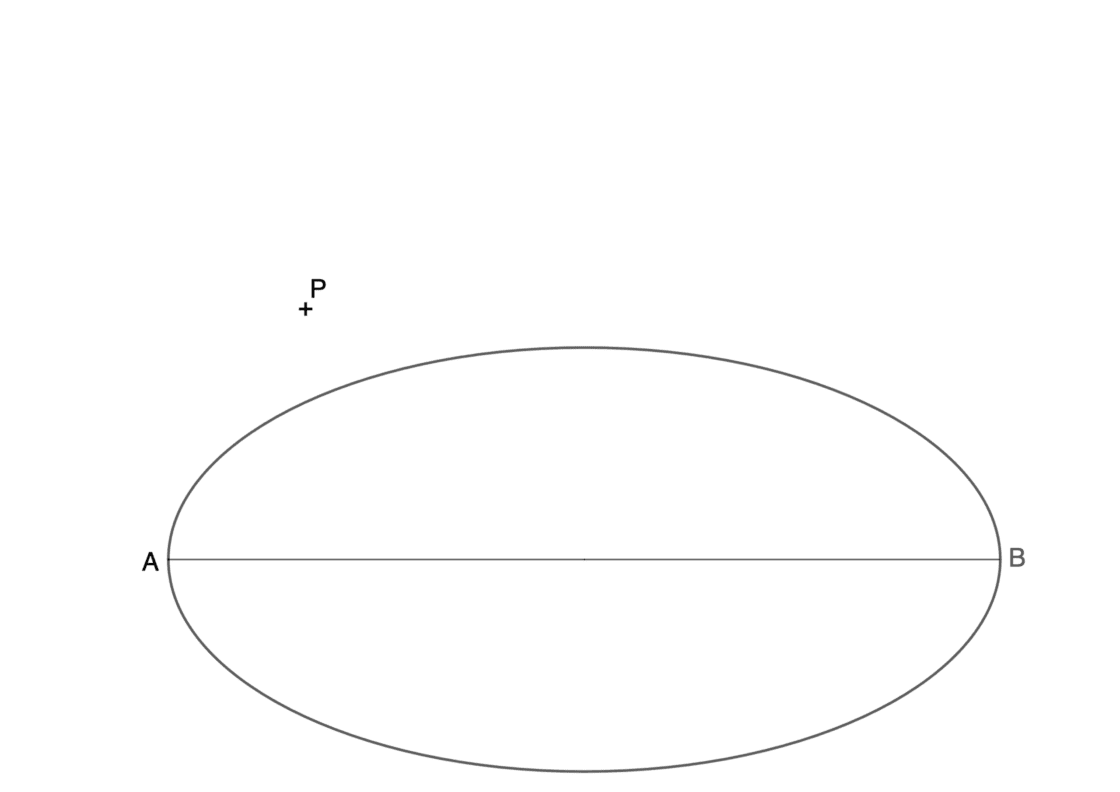
Al igual que en el ejercicio anterior, dibujamos una de las circunferencias focales de la elipse. En éste ejemplo he elegido la de F’. Acto seguido, con centro en P y radio PF dibujaremos un arco de circunferencia que corta a la circunferencia focal en los puntos Q y R.
Une los puntos Q y R con F’. En los puntos donde esos segmentos cortan a la elipse tienes los puntos de tangencia T1 y T2
Para terminar, solo tienes que dibujar las rectas que pasan por P y cada uno de los puntos de tangencia. En la aplicación interactiva de aquí abajo puedes mover los puntos A y B para cambiar el tamaño y forma de la elipse. También puedes mover el punto P para ver como se calculan sus tangentes.
Para que veas más claro el proceso, aquí tienes un vídeo donde explico el proceso completo. Si no sabes como hallar los focos de la elipse, puedes echarle un ojo a la sección de primero de bachillerato donde explico como hallar los focos de la elipse.
Rectas tangentes a una elipse y que son paralelas a una recta dada
En ésta ocasión, aparte de una elipse (o de la información para dibujarla) se nos proporciona una recta r y se nos solicita encontrar las rectas tangentes a la elipse que son paralelas a dicha recta. Tu punto de partida debería ser parecido a ésto:
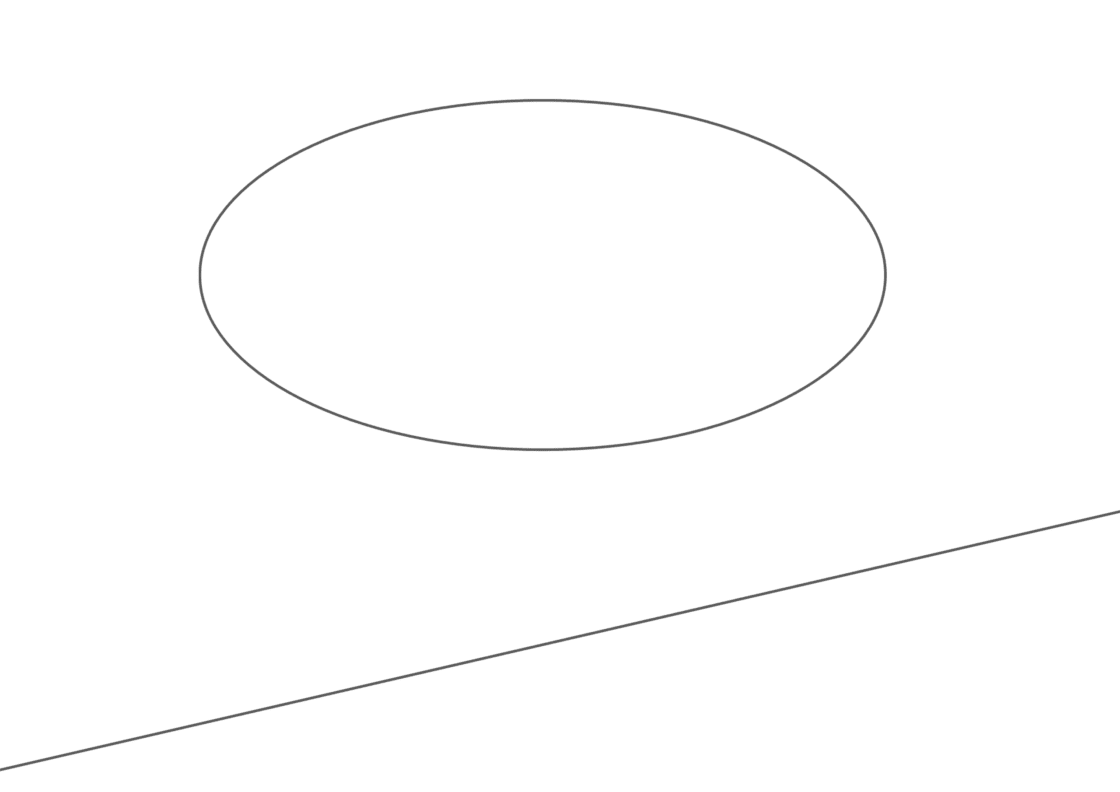
Como puedes comprobar, le he añadido un componente extra de dificultad al no proporcionarte ni los ejes ni los focos. Si no sabes como dibujarlos, te recomiendo visitar la entrada donde explico como hallar los ejes de una elipse.
Si no conocemos los focos, lo primero que debemos hacer es hallarlos. Una vez hallados éstos, dibujaremos la circunferencia focal por uno de los focos. Yo he dibujado la de F’.
Ahora dibuja una recta perpendicular a la recta r que pase por el otro foco. Los puntos donde corta la circunferencia focal que dibujaste antes son Q y R.
Si trazamos los segmentos F’Q y F’R, encontraremos los puntos de tangencia T1 y T2 en los lugares donde dichos segmentos cortan a la elipse. Ahora solo tienes que dibujar paralelas a la recta r que pasan por cada uno de esos puntos para hallar la solución.
Aquí tienes un vídeo donde puedes ver todo el proceso.
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti. Gracias de antemano por dejar tu comentario un poco más abajo.
