Antes de empezar con éste apartado deberías tener muy claro el procedimiento para resolver parábolas. Si no es así, es absurdo intentar comprender los métodos necesarios para dibujar una recta tangente a la parábola. Si ya has visto como resolver tangentes a otras curvas cónicas, date cuenta de que el procedimiento es el mismo. Solo tienes que recordar que la circunferencia focal de una parábola tiene su centro en el infinito.
Recta tangente a la parábola por un punto de la misma
Para éste tipo de ejercicios te suelen proporcionar una parábola ya dibujada y un punto que pertenece a la misma. Otra posibilidad es que te proporcionen el vértice, el foco y el punto, o bien el vértice y el eje y el punto y te pidan dibujar tanto la parábola como la recta tangente a la parábola. Para éste ejercicio vamos a suponer que ya tienes la parábola dibujada. Tu punto de partida se parecerá a ésto:
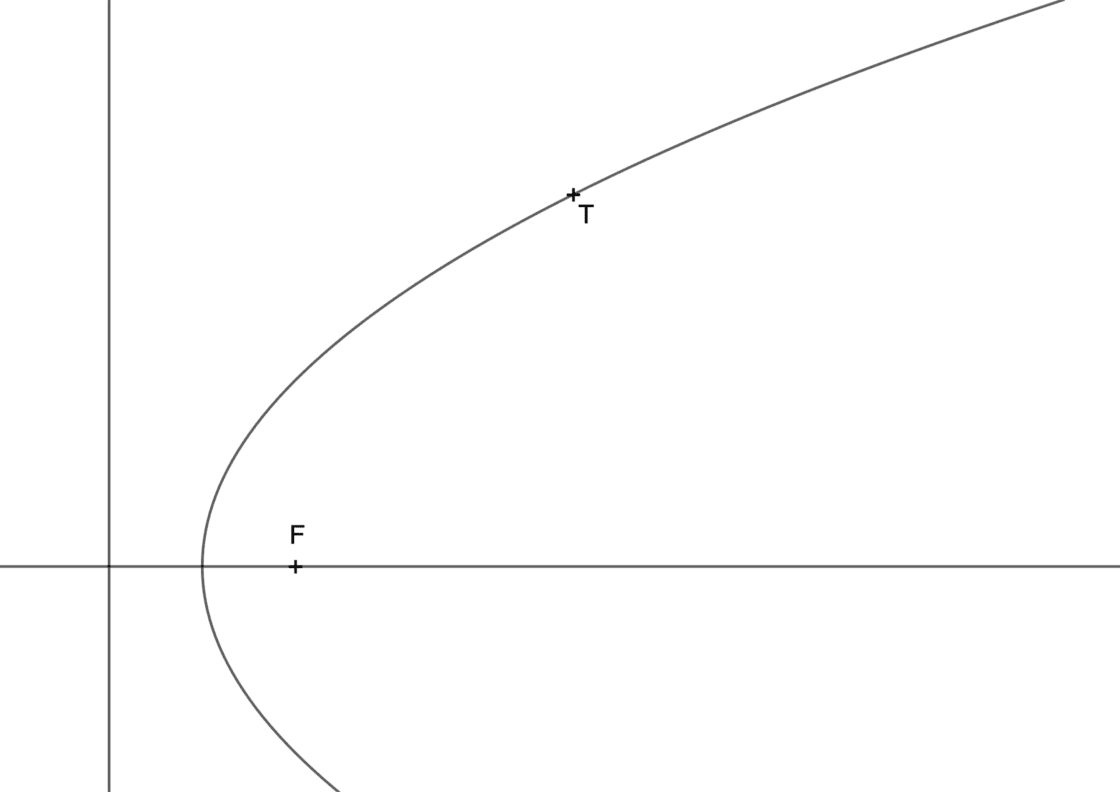
- Dibuja una paralela al eje que pase por T. Esta paralela corta a la circunferencia focal en A. Recuerda que en las parábolas la directriz hace la función de circunferencia focal.
- El punto A es simétrico al Foco respecto del punto T. Por ese motivo, si dibujas la bisectriz del ángulo que forman ATF tendrás la recta tangente a la parábola que te piden hallar. Si no recuerdas como hacer una bisectriz, siempre puedes hacer la mediatriz de AF y el resultado será el mismo.
En la siguiente imagen interactiva puedes mover el foco F y el punto T para comprobar las propiedades de la tangente a la parábola. También puedes hacer zoom con el ratón para alejar o acercar la imagen.
Aquí abajo tienes un vídeo explicando todo el proceso paso a paso.
Tangente por un punto exterior de la misma
En éste ejercicio las premisas y los datos que te proporcionan van a ser prácticamente los mismos que en el ejercicio anterior. La diferencia radica en que el punto no pertenece a la parábola, sino que es exterior a la curva cónica. Por ese motivo no habrá una recta tangente, sino dos. Tu punto de partida se parecerá a ésto:
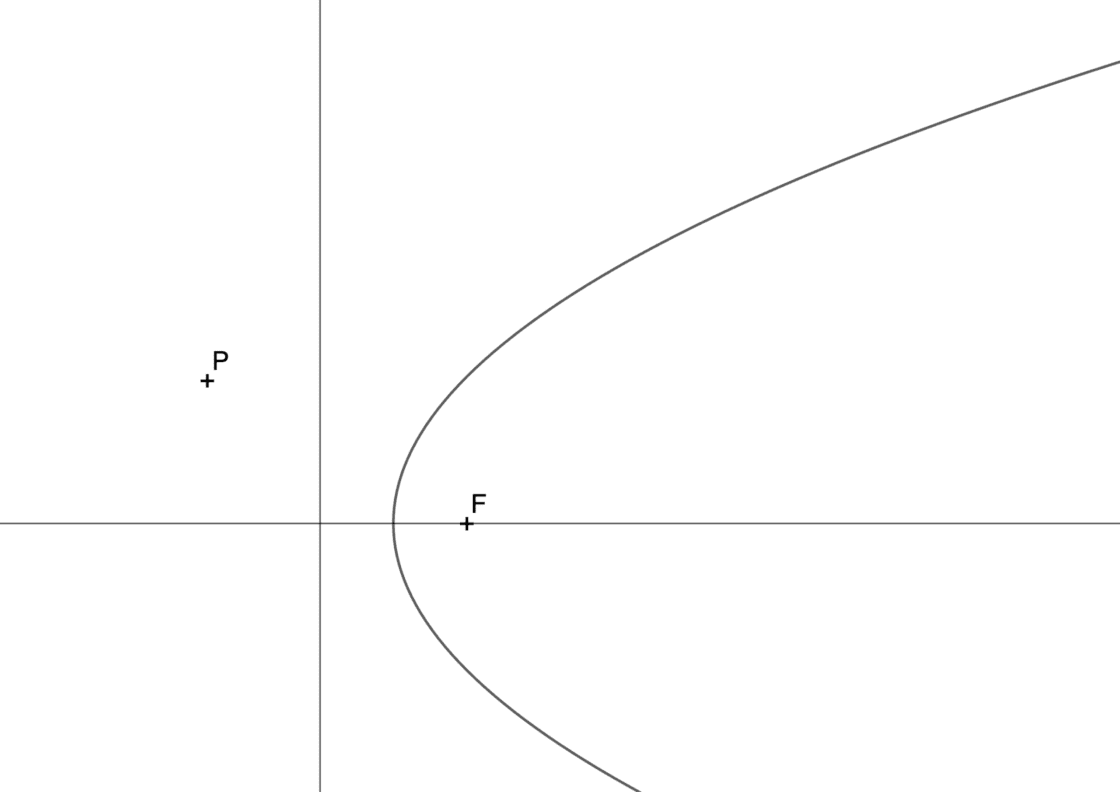
- Empieza por dibujar un arco con centro en P y radio hasta el Foco. Éste arco cortará a la circunferencia focal en los puntos A y B.
- La mediatriz de AF es la primera recta tangente a la parábola que te piden. La segunda será la mediatriz del segmento BF.
- Si quieres saber donde se encuentran los puntos de tangencia, solo tienes que hacer paralelas al eje que pasen por A y B. Los puntos donde cortan serán los puntos de tangencia T1 y T2.
En la siguiente imagen interactiva puedes mover el foco F y el punto P para comprobar las propiedades de la tangente a la parábola. También puedes hacer zoom con el ratón para alejar o acercar la imagen.
A continuación puedes ver un vídeo explicando todo el proceso anterior.
Tangente paralela a una dirección dada
Para éste ejercicio no te van a proporcionar un punto de tangencia, sino la dirección que sigue la recta tangente a la parábola. Tu punto de partida debe parecerse a lo que ves a continuación:
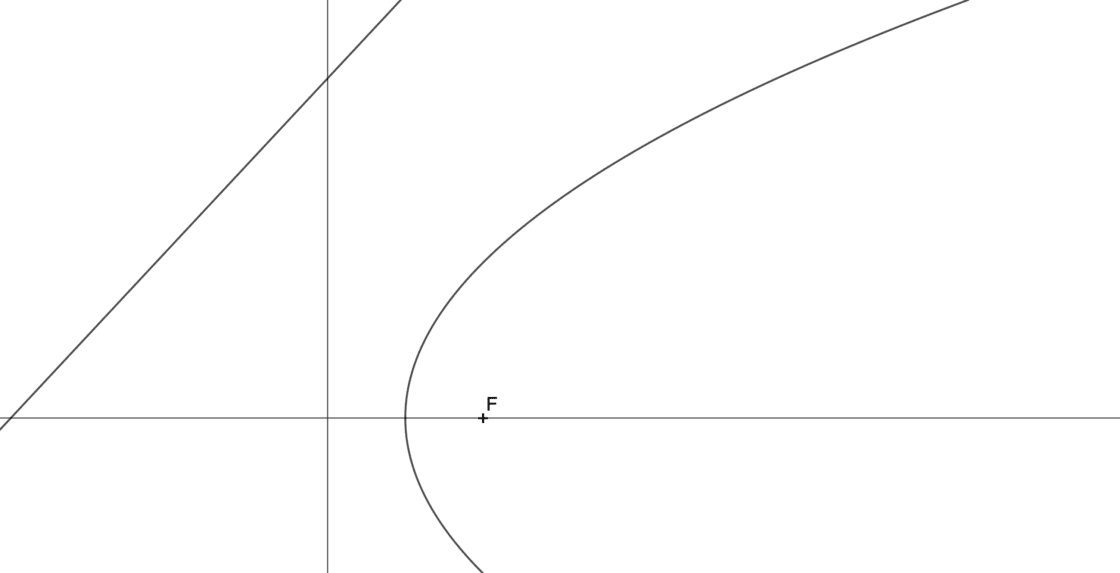
- Empieza por dibujar una recta perpendicular a la dirección dada y que pasa por el Foco. Verás que esa recta corta a la directriz en el punto A.
- Si dibujas la mediatriz de AF, tendrás la recta que te solicitan.
- Para hallar el punto de tangencia, dibuja una paralela al eje que pase por A. El punto donde corta a la parábola es el punto de tangencia T.
Otra posibilidad sería hallar el punto de tangencia primero y después hallar la bisectriz del ángulo que forman A, T y F.
En la siguiente imagen interactiva puedes mover el foco F y los puntos P y R para comprobar las propiedades de la tangente a la parábola. También puedes hacer zoom con el ratón para alejar o acercar la imagen.
El siguiente vídeo te explica todo el proceso paso a paso.
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
