En esta sección vamos a ver los tres tipos de problemas más comunes que nos podemos encontrar a la hora de resolver una recta tangente a la hipérbola. Saber solucionar este tipo de ejercicios también nos servirá para solucionar problemas de tangencias con curvas o circunferencias.
Recta tangente a la hipérbola por un punto que pertenece a la misma
Se nos da una hipérbola y un punto P que pertenece a la misma. También se suele conocer el eje real AB y los focos F y F’. Tu punto de partida será semejante a ésto:
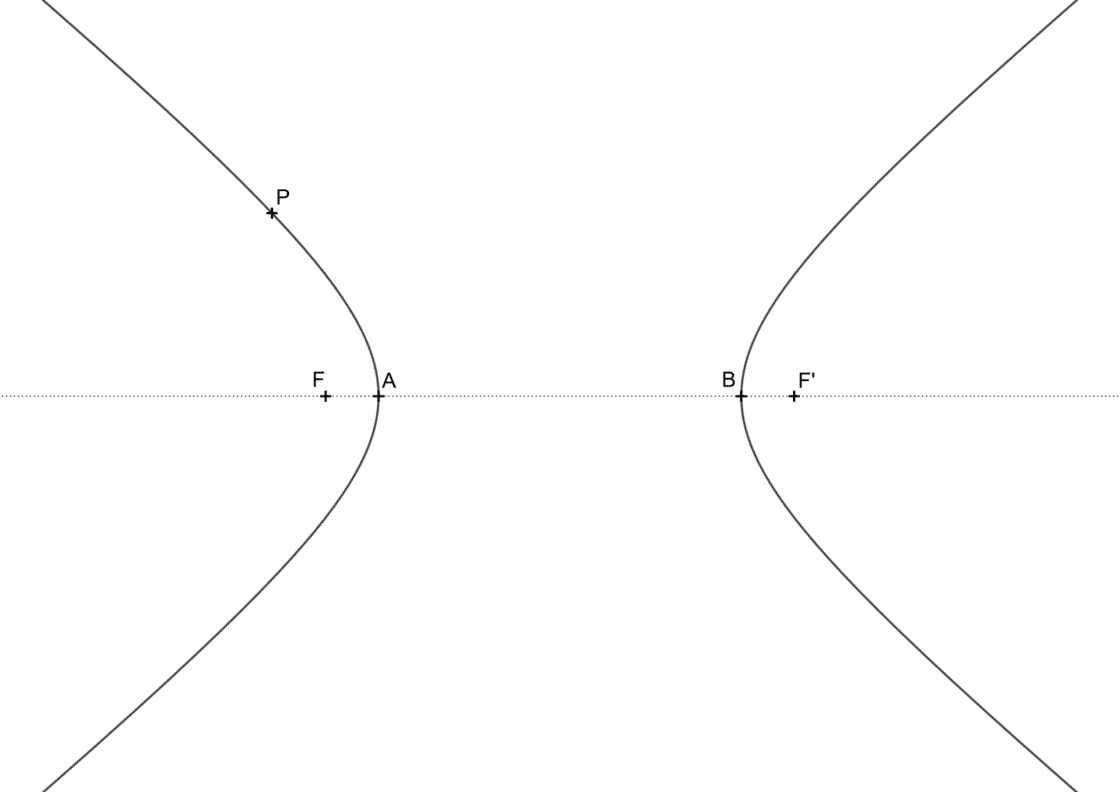
Este problema se puede solucionar de dos maneras distintas, una fácil y otra un poco más compleja, aunque no mucho. La primera y más sencilla es trazar la bisectriz que forman F, P y F’. De todas formas, este sistema no es demasiado fiable cuando el punto P está cerca del eje. En ese caso te toca resolverlo de la siguiente manera.
- Trazamos la circunferencia focal correspondiente a uno de los focos. Para este ejemplo puedes tomar la de F’.
- Une el foco F’ con el punto P, cortando a la circunferencia focal en el punto P’. El punto P’ es simétrico respecto al foco F, tomando como referencia la recta tangente buscada.
- Hallamos la mediatriz del segmento FP’, que será la recta tangente a la hipérbola que buscamos.
Rectas tangentes por un punto exterior
Se nos pide, dada la hipérbola de eje real AB y de focos F y F’, hallar las rectas que pasen por un punto P exterior y que sean tangentes a la hipérbola. Tu punto de partida será semejante a ésto:
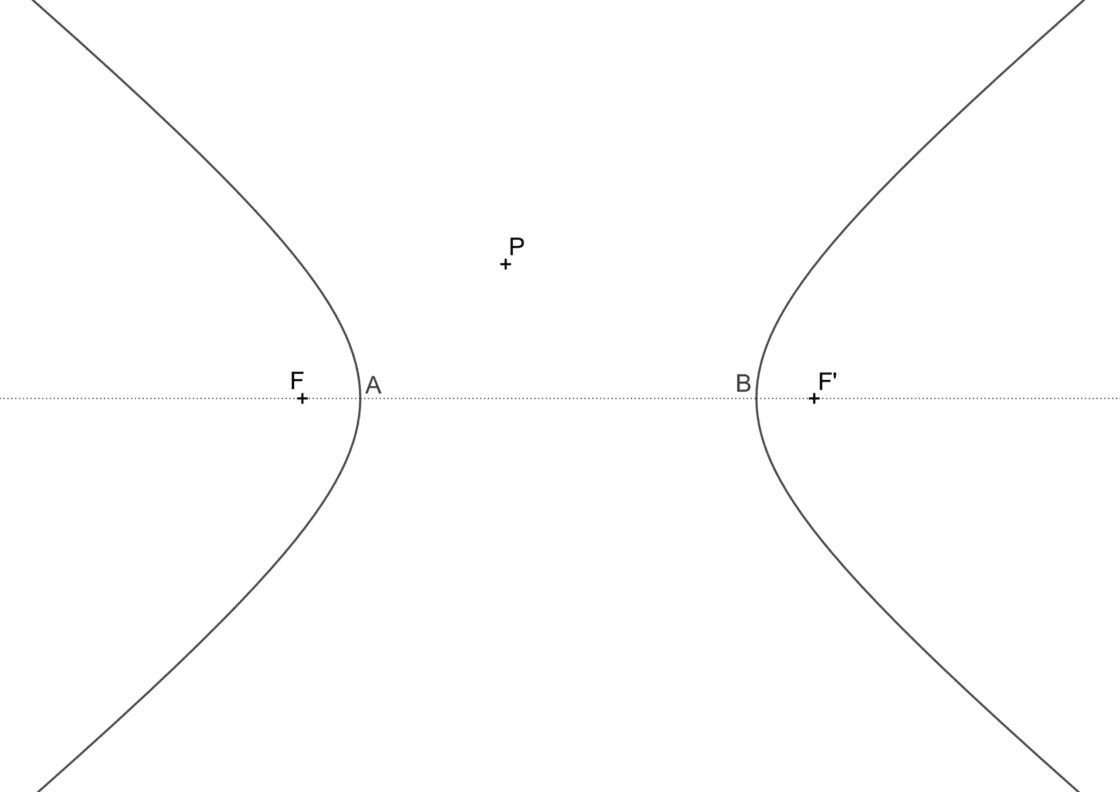
- Trazamos la circunferencia focal correspondiente a uno de los focos (yo he escogido la de F’).
- Con centro en el punto P dibujamos un arco de circunferencia que pasa por el otro foco (F). Este arco corta a la circunferencia focal en los puntos Q y R.
- La mediatriz del segmento FQ será la primera recta tangente a la hipérbola, y la mediatriz del segmento FR será la otra.
Si queremos hallar los puntos de tangencia T1 y T2 trazaremos rectas que pasen por F y Q y por F y R. Donde la recta que pasa por F’ y R corta a la recta tangente y a la hipérbola tendremos el primer punto de tangencia T1. En el punto donde la recta que pasa por F’ y Q corta a la recta tangente a la hipérbola tendremos el punto T2 de tangencia.
Si todavía tienes dudas, aquí abajo tienes un vídeo explicativo que espero que te aclare las ideas.
Rectas paralelas a una dada y tangentes a la hipérbola
Para este tipo de ejercicios de tangentes a una curva cónica partimos como en anteriores de una hipérbola conocida, su eje real AB y los focos F y F’. De forma adicional se nos proporciona una recta concreta r, y se nos pide hallar las dos rectas que son paralelas a la recta r y que son tangentes a la hipérbola. Así pues, tu punto de partida será semejante a ésto:
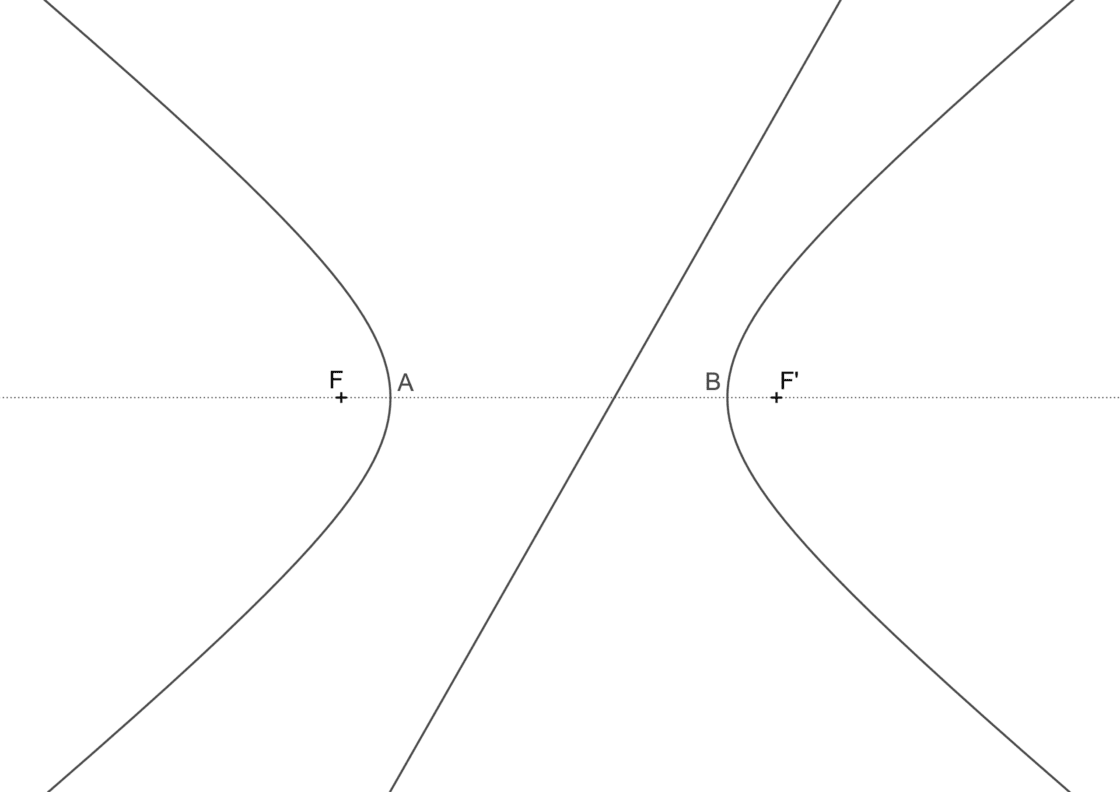
- Trazamos una circunferencia focal por uno de los focos. En nuestro caso hemos elegido el foco F, pero da igual el que se escoja.
- Desde el otro foco trazamos una recta perpendicular la recta r que corta a la circunferencia focal en los puntos R y S.
- La mediatriz del segmento F’R es la primera recta tangente a la hiperbola de las que se nos solicitan, y la mediatriz del segmento F’S será la otra.
- Si queremos hallar los puntos de tangencia, trazaremos una recta que pase por R y F y otra que pase por S y F. Los puntos donde cortan a las rectas tangentes serán los puntos de tangencia buscados T1 y T2.
Aquí abajo tienes una aplicación interactiva con la solución. Puedes mover los puntos C y D para cambiar la dirección de la recta dada, y el punto F’ para cambiar la hipérbola.
Y si todavía tienes dudas de como se resuelve este ejercicio, aquí abajo tienes un vídeo con todo el proceso resuelto paso a paso.
