Al igual que pasaba con el abatimiento de puntos, cuando se habla de abatimiento de rectas y segmentos en sistema diédrico nos estamos refiriendo a abatir una recta o segmento contenida en un plano. Recuerda que para dibujar este tipo de elementos necesitas dos puntos.
Abatimiento de rectas sobre el plano horizontal
El tipo de problema más sencillo es en el caso de rectas contenidas en planos cuando conocemos sus trazas, ya que podemos utilizar una de ellas como punto doble. El otro punto sería el que abatimos para solucionar el problema. En este caso tomaremos la traza horizontal del plano como charnela, y abatiremos la traza vertical de la recta, el punto V2. El procedimiento es el siguiente:
- Traza una línea perpendicular a la traza horizontal del plano que pase por V1.
- Ahora, con centro en O y radio hasta V2, traza un arco que corte a esa perpendicular en el punto V’.
- Si unes H1 con V’ ya tienes el abatimiento de la recta.
Date cuenta de que el segmento entre H1 y V’ representa la verdadera magnitud de la parte visible de la recta. Lo que se extiende hacia la izquierda sería lo que corresponde a la parte de la recta más allá del segundo diedro y que quedaría oculta.
Abatimiento de segmentos sobre el plano horizontal
Este método te sirve tanto para abatir segmentos, como para abatir rectas cuando no conoces sus trazas o quedan fuera del plano. Date cuenta de que en este segundo caso, deberías marcar dos puntos aleatorios sobre la recta que serían los que abatirías. Luego solo tendrías que unirlos una vez abatidos para tener el abatimiento de la recta. Tu punto de partida sería algo parecido a lo siguiente:
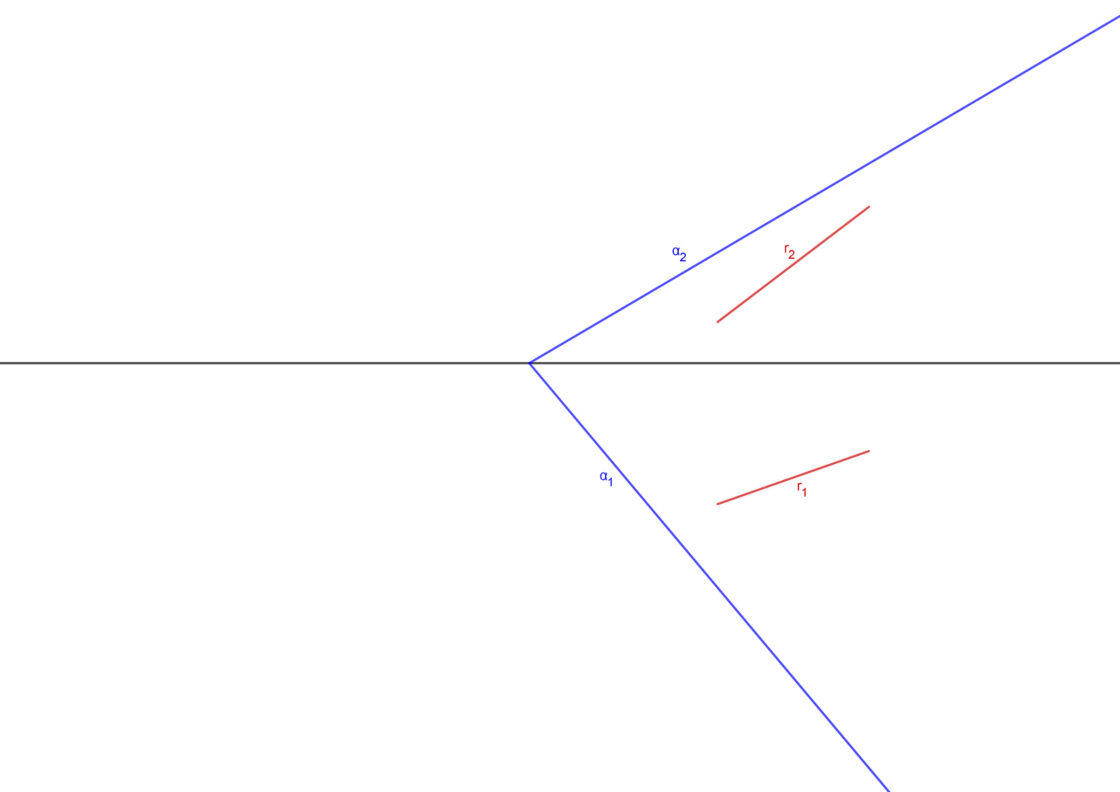
- Empieza por dibujar una recta horizontal que pase por cada uno de los puntos. De esa manera determinas los puntos T2 y T1 por un lado, que son la traza vertical de esa recta que pasa por B. Por otro lado obtienes S2 y S1, que son la traza vertical de la recta horizontal que pasa por A.
- Ahora toca abatir la traza vertical del plano α2 sobre el plano horizontal. Para ello dibuja una línea perpendicular a la traza horizontal α1 del plano que pase por S1.
- Acto seguido dibuja un acto con centro en O y radio hasta S2. Donde ese arco corta a la línea que trazaste en el paso anterior tienes el punto S’. Uniendo O con S’ tienes el abatimiento de la recta que representa la traza vertical del plano, que podemos llamar α’.
- Dibuja una línea paralela a la traza horizontal del plano que pase por S’, y una perpendicular a esa misma traza que pase por A1. Donde esas dos líneas se cortan tienes el punto A’, que es el abatimiento de A sobre el plano horizontal.
- Para continuar, dibuja una paralela a la línea que determina la traza horizontal del plano que pase por T’. Luego traza una recta perpendicular a esa traza que pase por B1. Donde ambas rectas se cortan tienes el punto B’, que representa el abatimiento del punto B sobre el plano horizontal.
El segmento entre A’ y B’ representa el abatimiento del segmento AB sobre el plano horizontal, y por tanto su verdadera magnitud.
Date cuenta de que estos procesos son reversibles. Esto significa que puedes tener una figura cualquiera representada sobre el plano horizontal (un cuadrado, por ejemplo) y puedes realizar el abatimiento en sentido inverso para descubrir como se vería sobre un plano concreto. Esto se conoce como abatimiento inverso o desabatimiento.
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
