Abatimiento de puntos en sistema diédrico

Antes de empezar, debes recordar que cuando ves una forma cualquiera en sistema diédrico, no verás su verdadero tamaño a menos que esa forma esté sobre los planos proyectantes o en paralelo a ellos. Así pues, si quisieras saber el verdadero tamaño de algo, solo tienes dos opciones. Mover el elemento en cuestión hasta ponerlo sobre los planos proyectantes o paralelo a ellos. La otra opción sería mover los planos proyectantes. Este segundo método lo explicaré en otra entrada, se denomina cambio de plano.

¿Qué es un abatimiento en sistema diédrico?

Cuando hablamos de abatimientos en sistema diédrico nos referimos a mover algo (por lo general una forma plana) para hacerlo coincidir con los planos proyectantes. Otra forma sería moverlo para situarlo en paralelo a los planos proyectantes. De esa manera podremos conocer sin problema su verdadera magnitud. A la hora de girar los planos o distintos elementos se toma como referencia una recta, a la que se denomina charnela. Este método no solo nos permite conocer los verdaderos tamaños. Date cuenta de que al conservar los tamaños, también conserva los ángulos.

Aunque más adelante te voy a explicar como abatir puntos y rectas en sistema diédrico, ten en cuenta que estos términos no son exactos. En realidad lo que haremos será abatir los planos que contienen a esos elementos.

Para abatir se utilizan dos métodos distintos, pero que son igual de válidos. El primero sería el método general, y el segundo sería el método reducido. Yo te explicaré ambos, en caso de que te los soliciten. Si no es así, te recomiendo que te centres en uno de ellos y utilices siempre el mismo. Mi consejo es que uses el que más sencillo te parezca.

Abatimiento de un punto sobre el plano horizontal

En si este es un ejercicio un poco simple y poco habitual. Pero es necesario conocer como abatir un punto porque una recta se forma con dos puntos, un triángulo con tres, y así sucesivamente.

Abatir un punto usando el método general

Este método es el más utilizado. Casi todos los vídeos que vas a encontrar en Youtube explicando problemas de abatimientos se basan en este sistema. Tiene su fundamento en el hecho de que la distancia existente entre O y V permanece constante antes, y después del abatimiento. A continuación tienes una imagen que creo que te aclarará un poco las ideas.

El tipo de problema que te puedes encontrar en este caso sería el siguiente: Halla la distancia entre el punto P y la recta r, teniendo en cuenta que la recta r se encuentra sobre el plano horizontal. Tu punto de partida será algo semejante a lo siguiente.

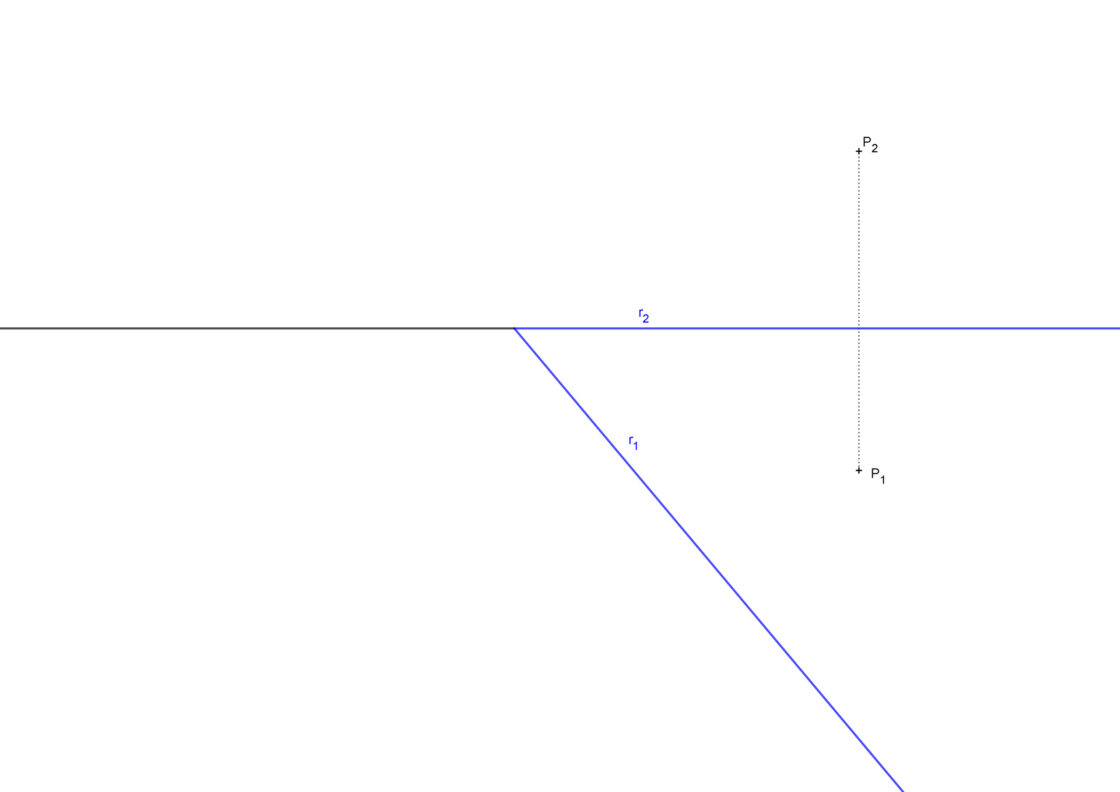
1. Empieza por hallar la traza vertical del plano que forman la recta r y el punto P. Esto lo puedes hacer con una recta horizontal. Así determinas el punto R, representado por sus proyecciones R₂ y R₁.
2. Uniendo O con R2 tienes la traza vertical del plano que forman r y P, que es lo que quieres abatir.
3. Dibuja una perpendicular a la proyección horizontal r₁ de la recta r.
4. Ahora marca con el compás en O y abre hasta R2. Traza un arco hasta cortar a la perpendicular que trazaste en el paso anterior. Donde se cortan tienes el punto R’.
5. Continua trazando una paralela a r₁ que pase por R’.
6. Para terminar, dibuja una perpendicular a r₁ que pase por P₁. Donde esa recta corta a la que dibujaste en el paso anterior, tienes el punto P’.

La distancia entre r1 y P’ es la distancia real a la que se encuentran el punto P y la recta r.

Abatir un punto usando el método reducido

1. Empieza dibujando una recta horizontal, igual que en el ejercicio anterior.
2. Traza una perpendicular a r₂ que pase por P₁. El punto donde corta a r₂ llámalo S.
3. A partir de P1, mide la altura del punto P. Esta medida también se define como la cota del punto. Así obtienes el punto T.
4. Con centro en S y radio hasta T, traza un arco que corte a la perpendicular que trazaste en el paso 2. El punto de corte es P’.

La distancia entre P’ y S es la verdadera magnitud de la distancia existente entre la recta r y el punto P.

Abatimiento de un punto sobre el plano vertical

Este tipo de procedimientos son muy similares a los que acabas de ver más arriba. La diferencia principal radica en que el plano se abate utilizando como charnela la traza vertical del plano. Por tanto las medidas las tomaremos en la parte superior de la línea de tierra, la que corresponde a las alturas.

Abatir un punto sobre el plano vertical usando el método general

El principio en el que se basa este ejercicio es el mismo que te explicaba un poco más arriba. El procedimiento es prácticamente el mismo.

1. Empieza por trazar una recta frontal contenida en el plano que pase por P. De esa manera determinas el punto R.
2. Traza una recta perpendicular a la traza vertical del plano que pase por R₂.
3. Con centro en O, traza un arco de circunferencia de radio hasta R₁. Donde ese arco corta a la perpendicular que trazaste en el paso anterior tienes el punto R’.
4. Dibuja una perpendicular a la traza vertical del plano que pase por P₂.
5. Para terminar dibuja una línea paralela a la traza vertical del plano que pase por R’. Donde esta línea corta a la anterior tienes el punto P’, que es el abatimiento del punto P.

Abatimiento de un punto sobre el plano vertical usando el método reducido

El método reducido para el abatimiento de un punto sobre el plano vertical no es muy diferente del proceso que se sigue cuando se abate sobre el plano horizontal.

1. Dibuja una recta frontal que pase por P. La necesitarás más tarde.
2. La distancia entre el punto R y P₁ determina el alejamiento, que en este caso puedes llamar a.
3. Traza una perpendicular a la traza vertical del plano que pase por P₂. Donde esa recta corta a la traza vertical del plano tienes el punto S.
4. Sobre la proyección vertical de la recta frontal que dibujaste en el primer paso tienes que medir contando desde P₂, el alejamiento. Es decir, el segmento a. De esa manera obtienes el punto T.
5. Con centro en S y radio hasta T, traza un arco que corte a la perpendicular que pasa por S y P₂. Donde se cortan encuentras el punto P’.

La distancia existente entre S y P’ determina la verdadera magnitud del segmento que forman S y P₂.