Hipérbola

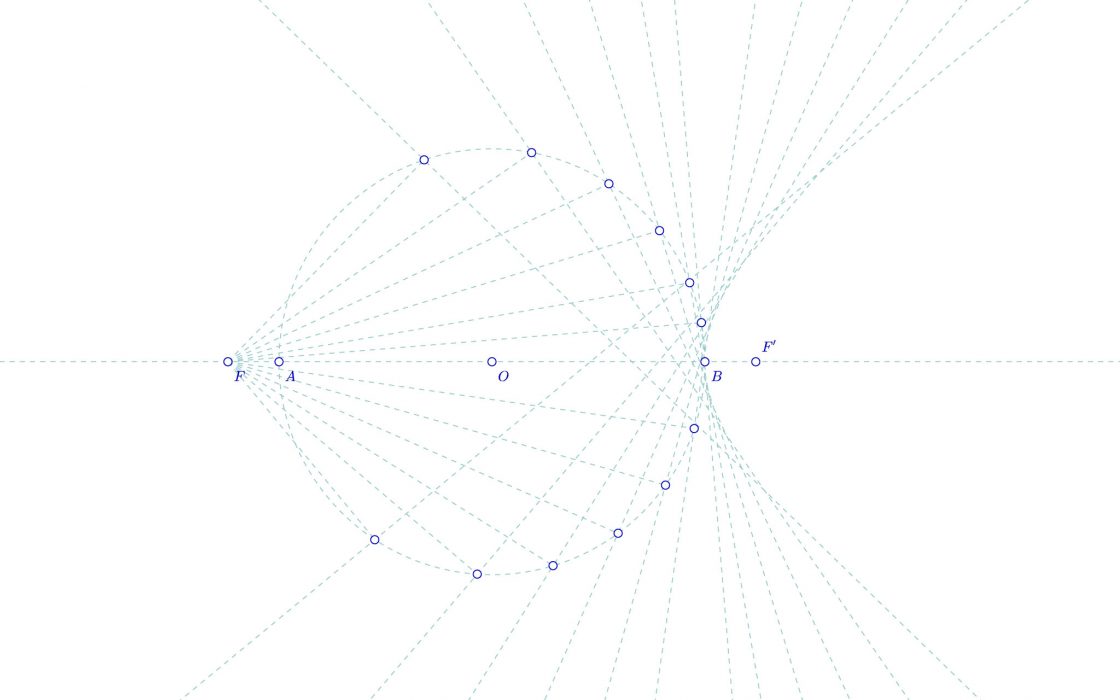
La hipérbola es una curva plana abierta, con dos ramas. Es una curva cónica que se define como el lugar geométrico de los puntos cuya diferencia de distancias a otros dos fijos, llamados focos, es constante e igual a 2a, siendo 2a igual al segmento AB, que es la longitud del eje real. Al igual que en la elipse, a los focos se les suele denominar F y F’. En la siguiente aplicación interactiva puedes mover el foco F y el punto A para modificar la Hipérbola. También puedes mover el punto P para comprobar que siempre se cumple que FP – PF’ = AB.

Tiene dos ejes que son perpendiculares y se cortan en el punto O, que es el punto central de la curva. El eje AB se suele representar como 2a y se denomina eje real. Los focos F y F’ siempre se encuentran sobre éste eje. La distancia entre focos FF’ se suele representar como 2c.

Por su parte, al eje CD de la hipérbola se le denomina eje imaginario y se le suele representar como 2b. Se le llama imaginario porque no tiene puntos comunes con la curva.

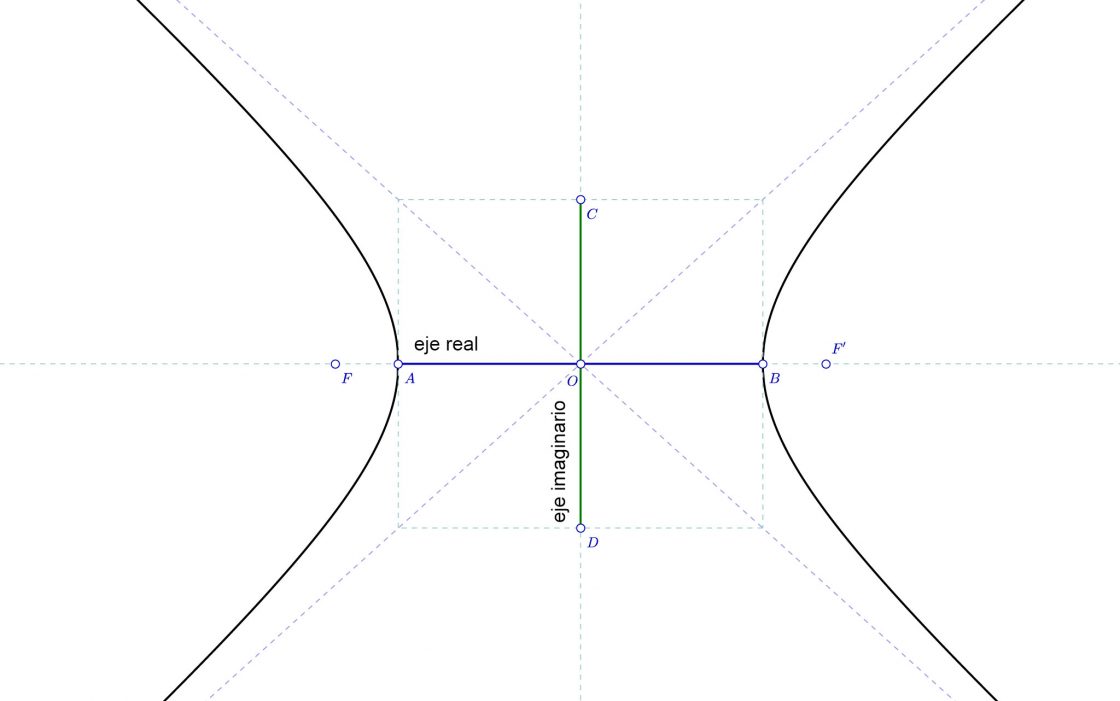
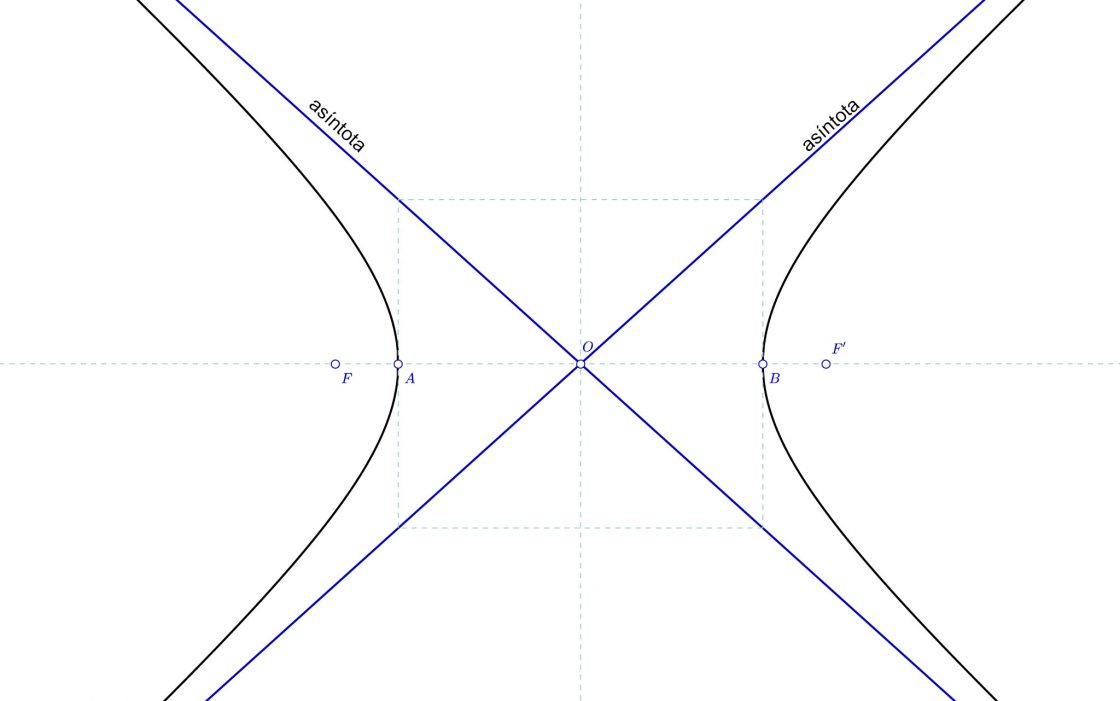
Como podéis comprobar, si construimos un rectángulo con altura igual al eje imaginario, y anchura igual al eje real, y que tenga por centro el punto O, rectas que pasan por las diagonales de dicho rectángulo serán las asíntotas. En caso de que no conozcas el tamaño del eje imaginario, hallar las asíntotas es muy sencillo. Todo lo que tienes que hacer es una perpendicular al eje por los puntos A y B. Luego dibujas una circunferencia con centro en O y radio OF. Si unes los puntos donde las perpendiculares cortan a esa circunferencia, tienes las asíntotas.

Propiedades de la hipérbola

Una propiedad interesante es que entre a, b y c siempre se cumple la relación de que c² = a² + b²

En la siguiente aplicación interactiva puedes verificarlo. Como aclaración, OF es igual a c. El segmento OA equivale al segmento a, y para terminar OC es el segmento b.

También es muy significativo que su trazado es simétrico respecto a los dos ejes, y por tanto también es simétrica respecto al punto central O.

Al igual que la elipse, se puede definir como el lugar geométrico de los centros de las circunferencias que pasan por un foco y que son tangentes a la circunferencia focal del otro foco.

Elementos notables

Vamos a comenzar por la circunferencia principal de la hipérbola. Ésta sería la circunferencia de radio a que tiene su centro en O. Se define como el lugar geométrico de los pies de las rectas que pasan por uno de los focos y son perpendiculares a las rectas tangentes de la hipérbola opuesta. Date cuenta de que los elementos notables repiten los mismos nombres y propiedades que los elementos notables de otras curvas cónicas, lo que te puede facilitar la tarea a la hora de aprender que son y como funcionan.

Las circunferencias focales tienen por centros los focos, y por radio un segmento de tamaño igual al eje real.

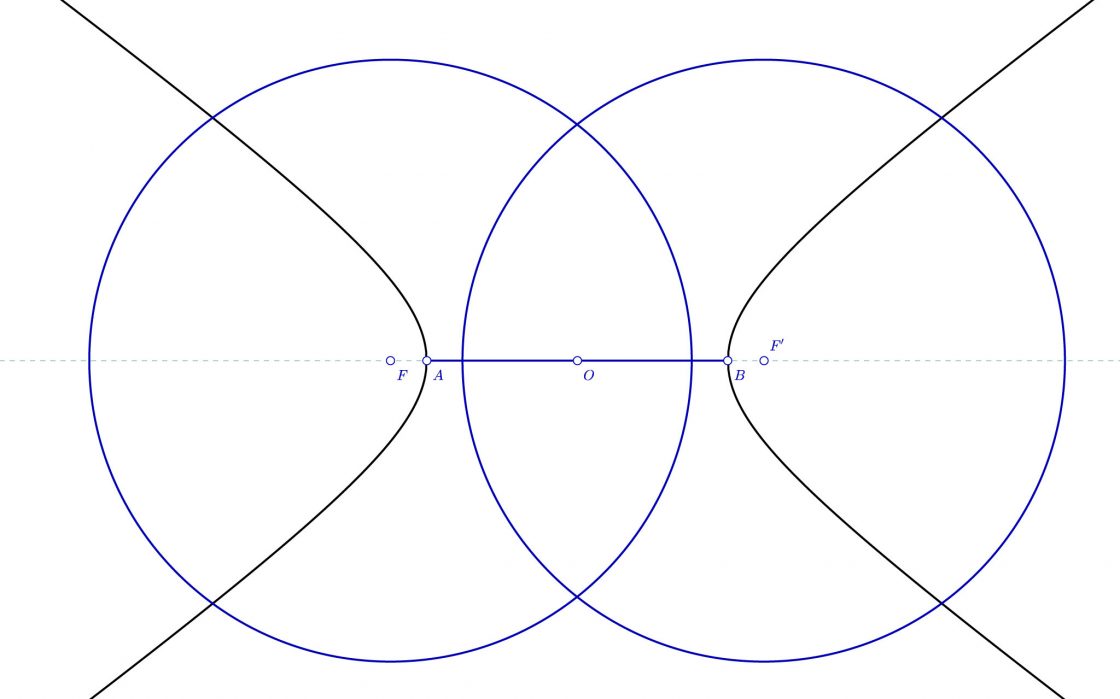
Los segmentos que unen cada uno de los puntos de la hipérbola con los focos se denominan radios vectores.

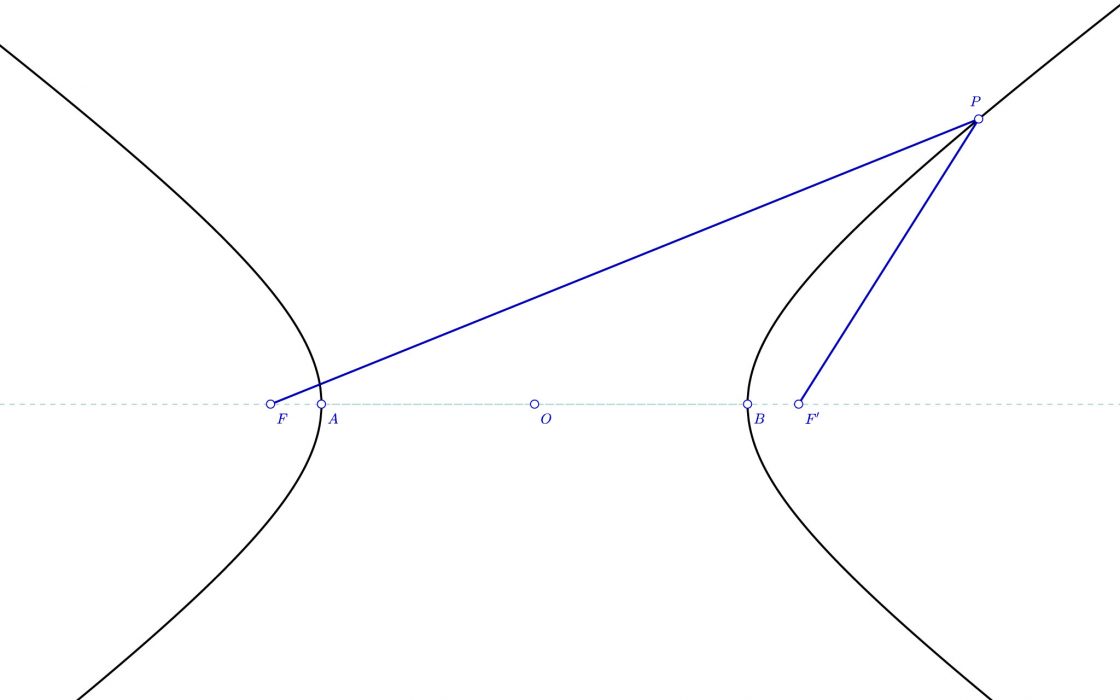
Las asíntotas son las tangentes a la curva en los puntos del infinito. Estas asíntotas son simétricas respecto de los ejes y pasan por el centro de la curva.

Construcción de una hipérbola conocidos los ejes y los focos

A continuación te voy a explicar como dibujar una hipérbola cuando conocemos el eje real y la distancia focal. Tu punto de partida debe parecerse a lo siguiente:

Marcamos un punto cualquiera C sobre la prolongación del eje real.
Con el compás pincha en el vértice opuesto A y mide hasta C.
Usando la distancia entre A y C como radio, dibuja dos arcos con centro en F y F’
Pincha en el vértice B y mide hasta C.
Con centro en F y F’, y radio igual a la distancia entre B y C traza dos arcos que cortarán a los dos que dibujaste antes en los puntos C₁, C₂, C₃ y C₄.
Con el compás pincha en el vértice opuesto A y mide hasta D.
Usando la distancia entre A y D como radio, dibuja dos arcos con centro en F y F’
Pincha en el vértice B y mide hasta D.
Con centro en F y F’, y radio igual a la distancia entre B y D traza dos arcos que cortarán a los dos que dibujaste antes en los puntos D₁, D₂, D₃ y D₄.
Con el compás pincha en el vértice opuesto A y mide hasta E.
Usando la distancia entre A y E como radio, dibuja dos arcos con centro en F y F’
Pincha en el vértice B y mide hasta E.
Con centro en F y F’, y radio igual a la distancia entre B y E traza dos arcos que cortarán a los dos que dibujaste antes en los puntos E₁, E₂, E₃ y E₄.
Uniendo todos esos puntos con la plantilla de curvas tendrás la hipérbola que buscas.

Puedes usar tantos puntos de referencia como necesites, aunque por lo general con tener tres bien repartidos es suficiente. Ten en cuenta que por cada punto obtendrás dos en cada rama de la hipérbola. Podemos situar los puntos de manera aleatoria o repartidos de manera proporcional, eso es lo de menos. Pero una vez tengamos una cantidad suficiente de puntos, podremos trazar la hipérbola.

Aquí abajo puedes modificar el punto A para modificar el eje real, y el punto F para modificar los focos. También puedes mover los puntos C, D y E para verificar la construcción.

A continuación tienes un vídeo explicando todo el proceso.

Construcción de la hipérbola conocidos el eje real y un punto de la misma

Para éste tipo de problemas el eje real AB y un punto de la hipérbola, pero desconocemos los focos. Para entendernos, nuestro punto de partida será algo similar a ésto.

Evidentemente no podemos utilizar el método de resolución que te he explicado antes, dado que no conoces la posición de los focos.

Unimos el eje real y lo prolongamos.
Trazamos la mediatríz de AB (luego la necesitaremos para hacer simetrías.
Dibujamos una perpendicular al eje que pase por P. Donde esa línea corta al eje tenemos el punto N.
Hacemos una perpendicular al eje que pase por B, y una paralela al eje que pasa por P. Donde esas líneas se cortan tenemos M.
Dividimos los segmentos MP y PN en un número de partes iguales. En éste ejemplo yo he dividido esos segmentos en cuatro partes iguales. A cada una de esas intersecciones llámalas 1, 2, 3… 1′, 2′, 3’…
Trazamos líneas que parten de A hasta cada uno de los puntos del lateral, y líneas desde B a cada uno de los puntos de arriba.
Donde el segmento que va de A hasta 3 corta a la línea que va de B hacia 3′ tenemos E₁
En la intersección del segmento de A hasta 2 y B hasta 2′ tenemos D₁
Para terminar, donde se cortan el segmento de A hacia 1 y el que va de B hacia 1′ tenemos C₁
El resto de puntos de la hipérbola los podemos obtener mediante simetrías respecto a los ejes.
Una vez que tienes todos estos puntos, puedes dibujar la hipérbola usando una plantilla de curvas.

Dibujar una hipérbola equilátera sabiendo los focos

En éste tipo de ejercicios, los datos que conoces son tan solo los focos de la hipérbola, y el hecho de que se trata de una hipérbola equilátera. En este caso la peculiaridad de esta construcción es que el eje real y el eje imaginario miden exactamente lo mismo, formando un cuadrado cuyo centro es el centro de la hipérbola. Por lo tanto, las asíntotas forman ángulos de 45 grados. Tu punto de partida será tan simple como éste:

¿Cómo lo puedes resolver?

Es mucho más sencillo de lo que parece:

Dibuja la línea que une F con F’, ya que sobre esa línea tendrás el eje real.
Halla la mediatriz de F y F’, porque sobre ella tendrás el eje imaginario, y en la intersección con la recta que dibujaste antes tendrás el centro O de la figura.
Con centro en O y radio hasta F ó F’, dibuja una circunferencia.
Como sabes que las asíntotas forman ángulos de 45 grados, puedes dibujarlas usando la escuadra.
Donde las asíntotas que dibujaste antes cortan a la circunferencia que tenías trazada de antes tienes los cuatro vértices del cuadrado.
Si unes los vértices que acabas de hallar entre si, donde cortan a la recta que une F y F’ tienes los vértices A y B.

A partir de éste punto, puedes trazar la hipérbola equilátera usando el método que te explicaba más arriba.

Trazado de la hipérbola por envolventes

Dados el eje real AB y los focos F y F’ construimos la circunferencia principal de centro O. Llegados a éste punto, solo tendremos que marcar puntos sobre la circunferencia principal, de forma proporcional o aleatoria (da igual). Trazar los segmentos que unen dichos puntos con el foco F, y después dibujar las rectas perpendiculares a dichos segmentos por los puntos de corte con la circunferencia.