Historia de la perspectiva cónica frontal
El sistema de representación espacial de la perspectiva cónica frontal es relativamente nuevo en la historia humana. El sistema cónico, también denominado lineal se estudia de manera científica en el siglo XV durante el renacimiento italiano. No obstante, existen evidencias históricas de que tanto romanos como griegos eran ya conscientes de la deformación a la que se ven sometidos los cuerpos con la distancia. Un buen ejemplo se puede apreciar en las columnas de los monumentos griegos. Lo que se denomina el éntasis.

Este sistema de representación se considera uno de los más perfectos que existen. Su utilización permite representar con gran fidelidad la visión humana sobre un lienzo. Pero no debemos olvidar que este sistema está ideado para ser observado desde un punto concreto del espacio. Os voy a poner un ejemplo…

Julian Beever es hoy dia, el artista más conocido dedicado al tema de la perspectiva cónica. Este tipo de imágenes aparecen deformadas cuando no se observan desde el punto de vista que el artista dispone.

Volviendo a la historia de la perspectiva cónica frontal. A pesar de ser conocidas las deformaciones y la existencia de los puntos de fuga, no serían estudiados de manera científica hasta comienzos del siglo XV por el arquitecto florentino Filippo Brunelleschi. Ente los años 1417 y 1427 realizó una serie de experimentos a través de los cuales promulgó una serie de teorías analizando los puntos de fuga y las deformaciones espaciales.

Posteriormente, las formulaciones propuestas por Brunelleschi fueron aplicadas, estudiadas y mejoradas otros grandes artistas. Entre ellos podemos destacar a Alberti, Paolo Uccello, Masaccio, y por supuesto, Leonardo Da Vinci.
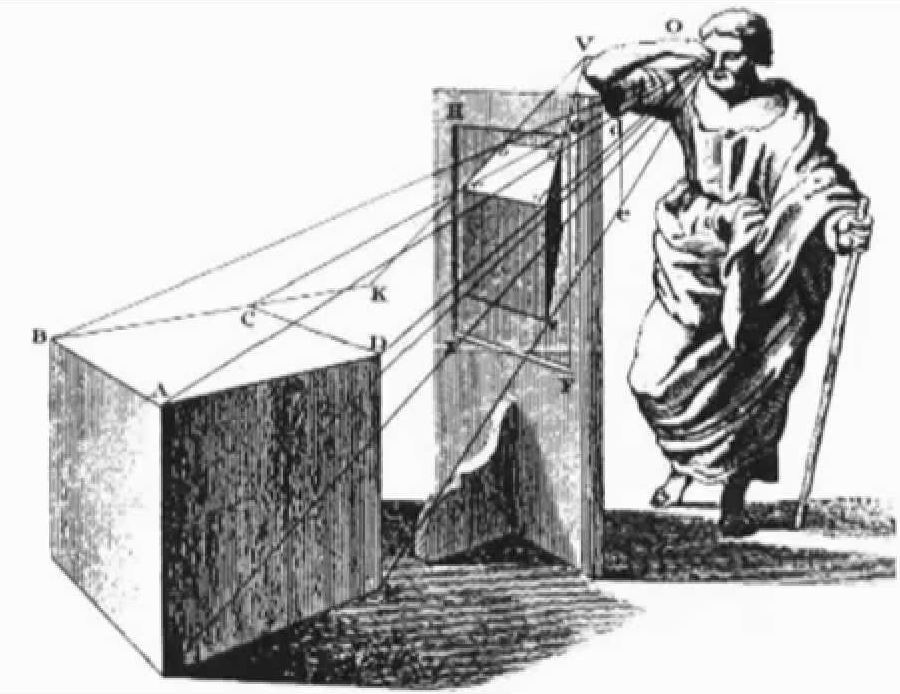
Este nuevo sistema fue utilizado con profusión en la elaboración de trampantojos. Estos juegos visuales permitían a los nobles de la época disfrutar de salones visualmente más grandes. Del mismo modo, podían tener decoraciones de apariencia tridimensional en espacios bidimensionales.

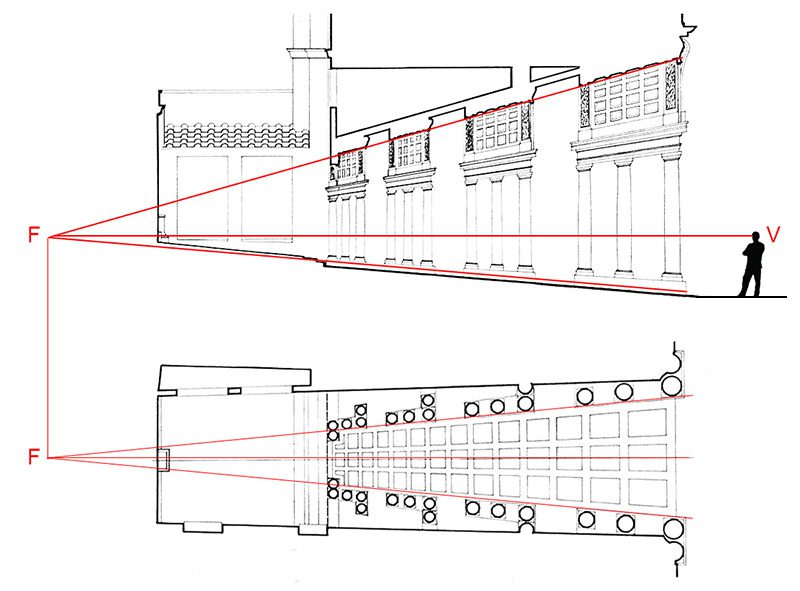
Pues resulta que si, son reales, pero responden a un uso muy inteligente de la perspectiva para dar la sensación de que su tamaño es mucho mayor de lo que es. Las últimas columnas del fondo son más pequeñas, pero el suelo asciende poco a poco, así como el jardín. De esa manera da la sensación de que su tamaño es mayor. En la siguiente fotografía puedes ver el tamaño real. Esta curiosa columnata la puedes encontrar en la Galería Spada en Roma.
Aquí abajo puedes ver una aclaración sobre este efecto que te ayudará a entenderlo.
Fundamentos y elementos del sistema de representación cónico de un punto de fuga
En primer lugar, aclarar porqué se denomina sistema de perspectiva cónica de un punto de fuga. Esto es así porque se fundamente en la proyección cónica, tomando el ojo del observador como el vértice de dicho cono.
Dicho esto, los elementos notables del sistema de perspectiva cónica frontal son:
Planos importantes en perspectiva cónica
- Plano del cuadro (PC): Es un plano vertical que suele colocarse entre el observador y el objeto (a veces el objeto está en parte por delante del plano de cuadro). Sobre él proyectamos el objeto y puede darse el caso de que el objeto se encuentre sobre el propio plano del cuadro.
- Plano Geometral (PG): Se podría interpretar como el suelo del cuadro. Sobre el situaremos los objetos que vamos a representar. En su intersección con el plano del cuadro obtenemos la Linea de Tierra.
- Plano del Horizonte (PH): Es perpendicular al plano del cuadro. Contiene el Punto de Vista y el Punto de Fuga o Punto Principal. En su intersección con el Plano del Cuadro nos proporciona la Línea del Horizonte.
- Plano de Desvanecimiento (PD): Es un plano que se encuentra perpendicular al Plano Geometral y paralelo al Plano del Cuadro. Contiene el Punto de Vista (los ojos del observador). Por detrás de éste plano no se pueden ver los objetos en la perspectiva cónica.
Líneas importantes en perspectiva cónica
- Línea de Tierra (LT): Es la línea que obtenemos de la intersección del Plano Geometral con el Plano del Cuadro.
- Línea del Horizonte (LH): Es la intersección del Plano del Horizonte con el Plano del Cuadro. Se encuentra separada de la Línea de Tierra por una distancia igual a la altura del punto de vista del observador.
Puntos importantes en perspectiva cónica
- Punto Principal (PP): En la perspectiva cónica frontal coincide también con el Punto de Fuga (PF). Es la proyección ortogonal del Punto de Vista sobre el Plano del Cuadro. Está contenido, por tanto, tanto en el Plano del Horizonte como el la Línea del Horizonte.
- Punto de Vista (PV ó V): Es el centro de la proyección de los haces proyectivos. Señala la posición de los ojos del espectador.
- Puntos de Fuga (F1 y F2): Son dos puntos situados en el Plano del Cuadro, sobre la Línea del Horizonte. Todas las rectas que sean paralelas a una misma dirección fugarán a éstos puntos. Son oblícuas al Plano del Cuadro.
- Puntos de Distancia (D1 y D2): Son dos puntos situados en el Plano del Cuadro, sobre la Línea del Horizonte. Están situados a la misma medida del Punto Principal que la separación del Punto de Vista al Plano del Cuadro. A éstos puntos fugan las líneas que forman un ángulo de 45 grados respecto al Plano del Cuadro. Se utilizan solo en la perspectiva cónica frontal o de un punto de fuga.
- Puntos Métricos (M1 y M2): Son dos puntos emparejados uno a uno con los Puntos de Fuga. Se utilizan para calcular la deformación de perspectiva de las medidas reales. Siempre y cuando las líneas fuguen a F1 y F2
Los Puntos Métricos se encuentran sobre la Línea del Horizonte y se calculan tomando la distancia de los Puntos de Fuga al Punto de Vista sobre la Línea del Horizonte. Estos puntos solo se utilizan en la perspectiva cónica oblicua o de dos puntos de fuga.
Distancias y direcciones importantes en perspectiva cónica
- Distancia principal: Es la distancia existente entre el Punto de Vista y el Punto Principal. Corresponde a la separación del observador con el Plano del Cuadro.
- Altura del horizonte: Es la distancia que existe (tomada en perpendicular) desde el Punto de Vista del observador al Plano Geometral. Nos delimita por tanto la separación entre la Línea del Horizonte y la Línea de Tierra.
- Distancia al objeto: Los objetos no tienen porque estar adyacentes al Plano del Cuadro. Esta es la distancia existente entre el vértice más cercano al espectador y el Punto de Vista, medida en planta. Esto es, paralelamente al Plano Geometral.
- Dirección principal: Es el ángulo que forman las caras proyectantes verticales del objeto respecto al Plano del Cuadro. Éste ángulo nos determina la inclinación del Plano del Cuadro respecto al objeto, teniendo en cuenta que el Plano del Cuadro es siempre perpendicular al Punto de Vista.
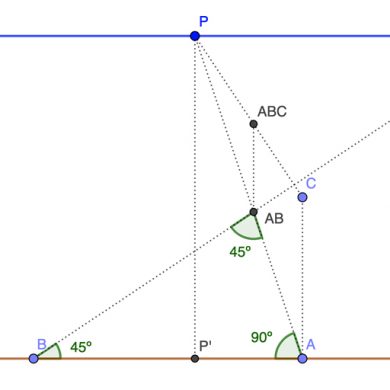
Aquí abajo tienes una aplicación interactiva que te permite cambiar el punto de vista, y con ello la distancia al plano del cuadro y la altura del espectador. También puedes modificar el punto de fuga para ver como se vería la figura si esta estuviera desplazada a la derecha o a la izquierda. Por último puedes mover los puntos azules del cubo para modificar su tamaño.
Como calcular distancias y profundidades en perspectiva cónica frontal
En el siguiente vídeo os explico como se calculan las distancias en perspectiva cónica frontal. Para ello realizaremos un sencillo ejercicio. Dibujar una alfombra cuadrada de 10x10cm. Los datos que necesitamos conocer son la altura del punto de vista, que nos determina la linea del horizonte. Se encuentra a 10cm sobre la línea de tierra. También la posición del espectador, que se encuentra centrado respecto a la figura. Por último necesitamos saber la distancia a la que se encuentra del plano del cuadro, que son 15cm.
Como calcular distancias y profundidades no unidas al plano del cuadro.
Este ejercicio de perspectiva cónica frontal es un poco más complejo que el anterior. En ésta ocasión vamos a dibujar una alfombra con un elemento decorativo central en forma de cuadrado. Las medidas son las mismas que en el ejercicio anterior, tanto para el Punto de Vista, Línea del Horizonte, Línea de Tierra y distancia al Plano de Cuadro. Las medidas del cuadrado interior son de 5cm de lado.
Cómo dibujar curvas y circunferencias
En el siguiente ejercicio vamos a ver como realizar curvas y circunferencias en perspectiva cónica frontal. Para ello vamos a dibujar una alfombra cuadrada decorada con una circunferencia del mismo diámetro que el lado del cuadrado (circunscrita).
Las medidas son las mismas que tenemos en los anteriores ejercicios.
Calcular profundidades correctamente en perspectiva cónica frontal
Si eres un poco observador, te habrás dado cuenta fácilmente del problema que supone la forma de representación que estoy utilizando hasta ahora. En efecto, dada la planta en diédrico, la figura saldrá invertida. Es decir, como reflejada en un espejo.
Tal vez no te has dado cuenta hasta ahora porque hasta ahora solo he utilizado figuras simétricas. ¿Pero que pasa cuando la figura no es simétrica? Pues que los puntos más cercanos al observador se representan más lejos del plano del cuadro, y ésto no es correcto.
Ahora que ya sabes tomar medidas en profundidad y entiendes los principios y el mecanismo para representarlos, ha llegado el momento de ir un paso más allá y representar la planta correctamente en profundidad.
El proceso es mucho más sencillo de lo que podría parecer. Vamos a ver como se realiza:
En primer lugar, vamos a trazar un plano auxiliar al plano de cuadro. Es decir, una línea paralela a la línea de tierra, pero que pase por el punto más cercano al espectador. Ese será el punto del objeto que se encontrará sobre el plano del cuadro, y a partir del cual vamos a construir el resto de la figura. Nuestro punto más cercano es el punto F, por lo tanto el plano auxiliar debe pasar por ese punto.
- Vamos a empezar por el punto A1
- En primer lugar proyectamos sobre el plano auxiliar, descubriendo A2
- Ahora, con centro en A2 y radio hasta A1 trazamos un arco que corta a la recta auxiliar en A3
- Esa es la medida que tenemos que tomar en profundidad. En el vídeo he realizado una perpendicular al plano de tierra, pero en realidad no hace falta. Ya tenemos la medida tomada con el compás, por lo que solo debemos marcarla sobre la línea de tierra.
- Ese nuevo punto que hemos marcado, al que llamaremos A4 es el que debemos llevar a D1 para hallar la representación del punto en perspectiva cónica frontal.
- El punto de corte con la línea de fuga nos determina A5 que será la representación de A1 en profundidad.
Si te fijas, para el resto de puntos solo tienes que repetir el mismo proceso. Ten en cuenta de todas formas, que muchos puntos los puedes solucionar gracias a rectas paralelas o perpendiculares a puntos conocidos. Esto es especialmente útil cuando se encuentran a la misma distancia del plano del cuadro o a la misma altura.
Como levantar alturas en el sistema cónico
Vamos a continuar el ejercicio anterior. Lo he dividido en varios vídeos para que no sea tan denso. En ésta ocasión te enseñaré el último paso; cómo levantar alturas. Ya sabes dibujar la planta en profundidad y correctamente. El último paso sería pues levantar las alturas si la figura no es plana (que nunca lo es). Para continuar desde donde lo dejamos, vamos a suponer que la planta que has dibujado antes tiene 5 centímetros de altura.
Para calcular la altura de puntos en perspectiva tenemos dos posibilidades. En primer lugar, podemos levantar verticales desde la planta y ver donde cortan con las líneas de fuga que dibujaremos desde el plano del cuadro.
Otra opción posible sería levantar líneas paralelas a la línea de tierra a las alturas que necesitamos. Si nosotros calculamos las profundidades desde esas distancias, obtendremos los puntos en altura y en profundidad.
Ejercicio real: Mesa Bjursta
En ésta ocasión te propongo un ejercicio de perspectiva cónica real. Representar un mueble de una conocida empresa tal y como lo vería una persona que midiera 150cm de alto y que se encontrara a 2 metros de la mesa. En la siguiente imagen veis las medidas de la misma.
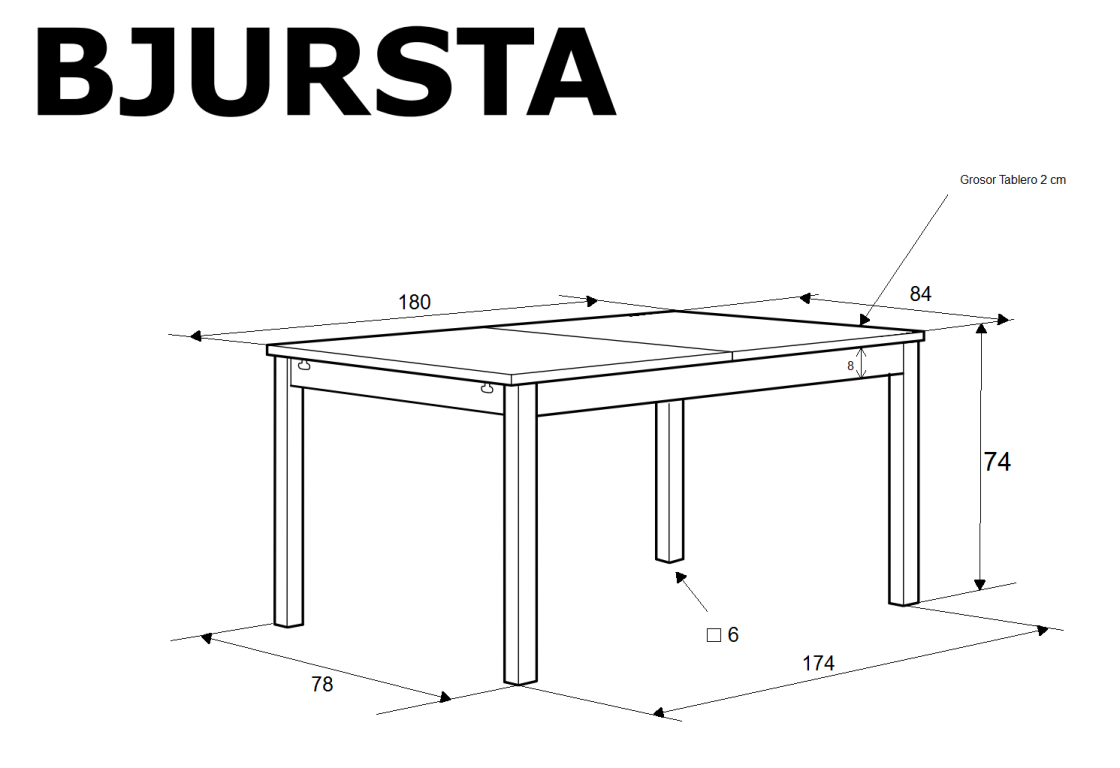
El el siguiente vídeo tienes el desarrollo completo del ejercicio. Me vas a permitir que no ponga la transcripción completa en éste caso, ya que sería demasiado largo y tampoco creo que aportara información relevante. No obstante, si te bloqueas con éste ejercicio, repasa los anteriores. Volver a recordar como medir distancias y calcular alturas te ayudará a resolver éste problema y te atascarás menos.
También te puede interesar…
Representación del punto en perspectiva cónica frontal
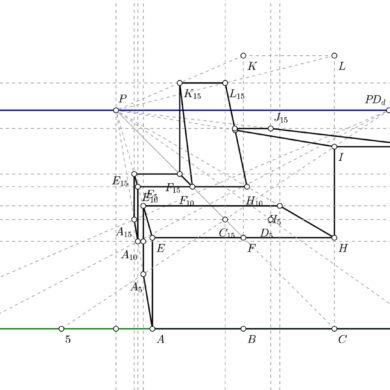
Ejercicio resuelto de cónica frontal
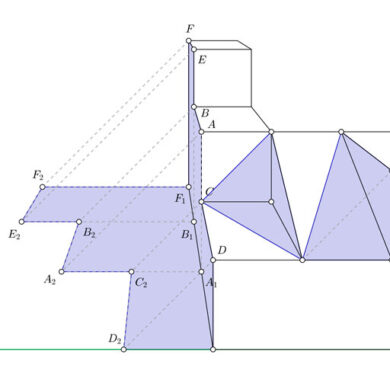
Sombras en perspectiva cónica frontal, punto impropio
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.

