En esta entrada vas a aprender como representar un punto cualquiera en perspectiva cónica oblicua, también conocida como perspectiva cónica de dos puntos de fuga. Como imagino que ahora mismo el tema de la perspectiva oblicua te suena a chino, vamos a empezar por el principio. Lo primero es entender que es cada punto, y como hallarlos.
Cuando trabajamos en perspectiva cónica de dos puntos de fuga, tenemos varios puntos importantes:
- La altura del observador, se suele representar con la letra P. Esta altura marca la Línea del Horizonte.
- Los pies del observador, lo más habitual es nombrarlo con la letra P’. Este punto te sirve para marcar la Línea de Tierra.
- La distancia al plano del cuadro. Te indica la separación del observador hasta el cuadro, lo más habitual es marcarlo con la letra V.
- Los puntos de fuga. Vas a tener dos, uno a la derecha y otro a la izquierda. Se suelen llamar PF1 y PF2. Yo para liar menos que quede todo más claro, me gusta llamarlos PFd y PFi. Es decir, Punto de Fuga Izquierdo y Punto de Fuga Derecho.
- También tenemos dos puntos de distancia. Estos sirven para tomar medidas. Ten en cuenta que al contrario de lo que pasaba en la perspectiva cónica frontal, a cada punto de fuga le corresponde un punto de medida. Solo puedes tomar medidas sobre el punto de distancia opuesto. Se suelen llamar PD1 y PD2, aunque yo prefiero llamarlos PDi y PDd para distinguirlos. Es decir, Punto de Distancia Derecho y Punto de Distancia Izquierdo.
- El ángulo que forma el plano del cuadro respecto a la figura a representar. Es muy importante porque nos sirve para hallar los puntos de fuga y distancia.
Preparando el terreno
Dicho esto, el primer paso es dibujar todos estos elementos antes de empezar a dibujar la figura. Si quieres repetir este ejercicio necesitarás una hoja A3. En éste ejemplo he considerado lo siguiente:
- Altura del observador: 10cm
- Distancia al plano del cuadro: 15cm
- Ángulo que forma el plano del cuadro: 30º a la derecha
Veamos como se hace:
La Línea de Tierra
Empieza por marcar la línea de tierra lo primero. Como en este tipo de ejercicios no es habitual tener nada por debajo del suelo, puedes poner la línea de tierra cerca del borde inferior de la hoja. Sitúa los pies del espectador sobre la Línea de Tierra. Este punto lo llamaremos P’. Si el ángulo que te dan es de 45 grados, lo mejor es ponerlo centrado. En caso de que el ángulo sea de 30 ó 60 grados, lo mejor es ponerlo a un tercio del borde. Según el que sea, a la derecha o a la izquierda.
La Línea del Horizonte
La Línea del Horizonte es paralela a la Línea de Tierra, y se encuentra a la altura del observador. Imagina que estás en una calle larga, y miras a lo lejos. Todas las líneas van a acabar a la altura de tus ojos. Midiendo en perpendicular desde el punto P’, marca el punto P, que delimita la altura del observador.
El Punto de Vista
Este punto representa la distancia a la que el observador se encuentra separado del plano del cuadro. Para dibujarlo debes prolongar la línea que une P’ con P. A partir de P, mide la distancia que corresponda, y sobre ella marcas el punto V.
Los Puntos de Fuga
Una vez que hemos puesto los elementos anteriores, es tiempo de poner los puntos de fuga. Debes hacer una paralela a la Línea del Horizonte por el punto de vista (Punto V). Sobre ella debes marcar el ángulo que te indique el ejercicio. Prolongando esa línea, te cortará a la Línea del Horizonte en un punto. Ese punto es el Punto de Fuga Derecho. Si haces una perpendicular a la recta que acabas de hacer, tendrás otro punto de corte. Ese nuevo punto será el Punto de Fuga Izquierdo.
Los Puntos de Distancia
Esta parte es fácil. Pincha sobre el Punto de Fuga Derecho con el compás, y abre hasta V. Haz un arco que corte a la Línea del Horizonte. Ese será el Punto de Distancia Derecho (aunque quede a la izquierda). Luego pincha con el compás en el Punto de Fuga Izquierdo y con radio hasta V traza un arco que corte a la Línea del Horizonte. Ese punto será el Punto de Distancia Izquierdo (si, se queda a la derecha).
A veces la distancia es muy grande y el compás no da tanto de si como para hacer el arco. En tal caso puedes hacer un arco cualquiera (mejor que sea grande). Marcas los puntos de corte, y dibujas la línea que los une. Luego haces una paralela a esa línea que pase por V. De esa manera obtienes el punto de distancia sin problemas.
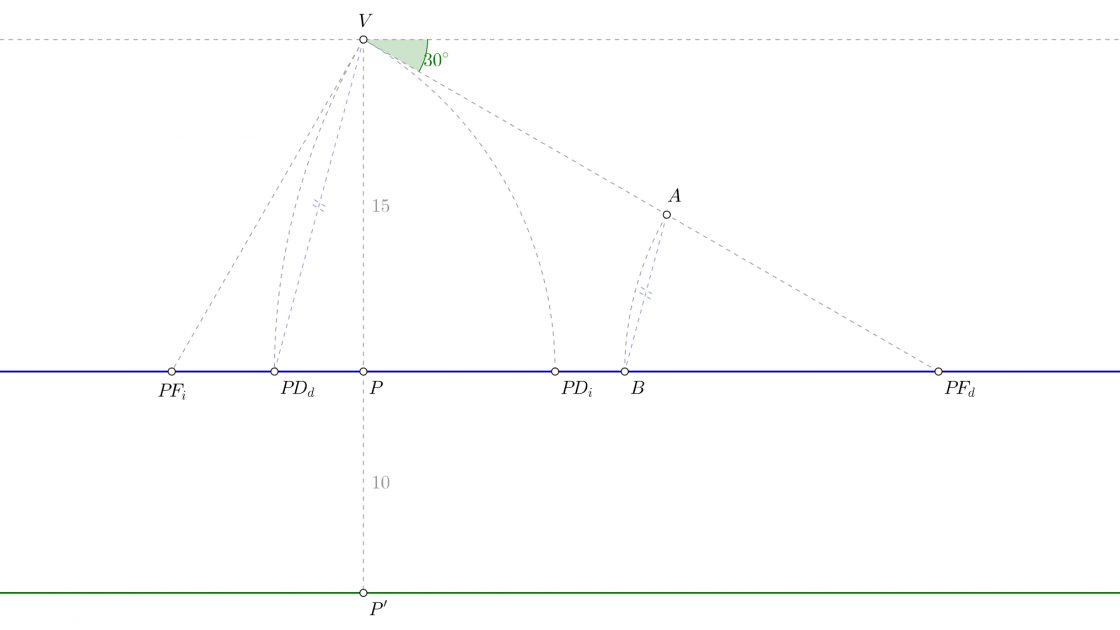
Representación del punto en perspectiva cónica oblicua
Si estás realizando éste ejercicio paso a paso, puedes utilizar los elementos que acabas de representar. Vamos a considerar que queremos hallar un punto que se encuentra a 7cm de anchura, a 4cm de profundidad y a 6cm de altura.
Lo primero que debes saber es que solo puedes realizar medidas sobre el plano del cuadro. Es decir, sobre la línea de tierra o la vertical que une P con P’. En ningún otro punto, de lo contrario la representación no será correcta. Dicho esto, usando la regla, mide hacia la derecha, a partir del punto P’ los 7cm de anchura. Luego mide 4cm a la izquierda, que representan la profundidad. Desde P’, sobre la vertical que le une con P, mide los 6cm de la altura.
Deberías tener algo parecido a esto.
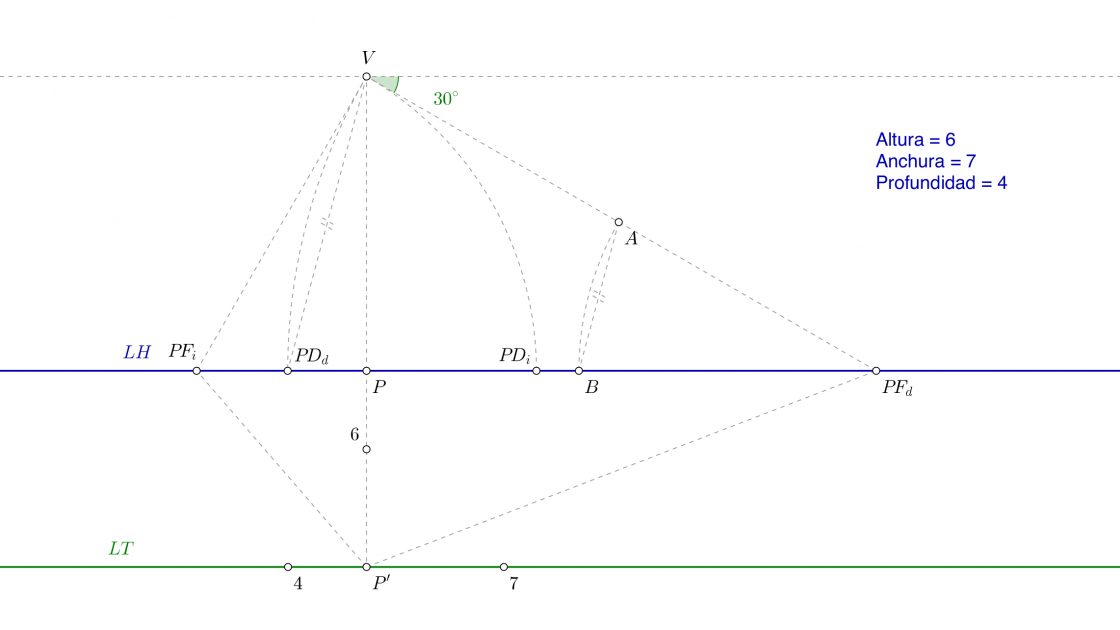
Primer paso: Anchura
Vamos a ir poco a poco. Para hallar cualquier anchura, debes medirla sobre la línea de tierra y hacia la derecha. Acto seguido, esa medida que has tomado (en este caso 7cm) la debes unir con el punto de distancia que le corresponde. Al contrario que en la perspectiva cónica frontal, no podemos usar cualquier punto de distancia. En el caso de la perspectiva de dos puntos de fuga, SIEMPRE debemos unir las medidas con el punto de distancia opuesto. Para no liarte, no marques toda la línea. Con que marques solo hasta el punto en que corta es suficiente.
Es muy importante que recuerdes que solo puedes medir las anchuras sobre la línea que va de P’ a PFd, y sobre ningún otro lado. Las líneas que nacen a la derecha del punto P’ y sobre la línea de tierra SOLO cortan con esa línea. Al punto de intersección lo vamos a llamar B. Debes tener algo parecido a ésto.
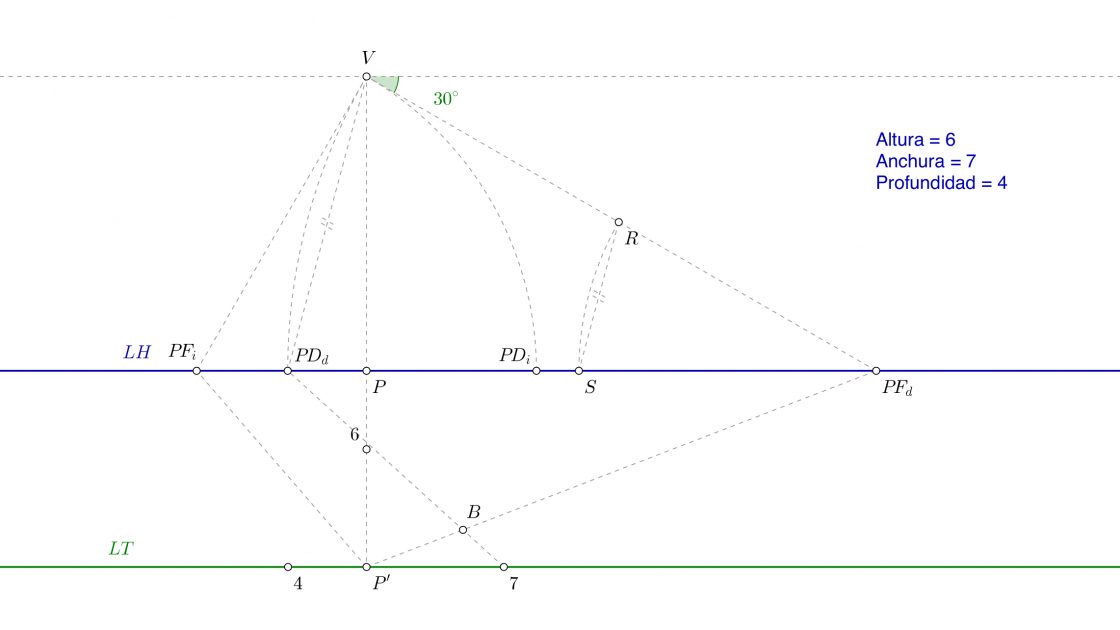
Segundo paso: Profundidad
El siguiente paso es hallar la profundidad. Recuerda que las profundidades las tomamos a la izquierda del punto P’, y sobre la línea de tierra. En este ejemplo eran 4cm que ya tenemos marcados. Dibuja la línea que une ese punto que representa los 4cm con el punto de distancia que le corresponde (recuerda, siempre el opuesto). De esa manera obtienes el punto A, que determinará esa profundidad de 4cm en perspectiva. Como en el caso anterior, no dibujes toda la línea. Realmente solo te interesa el punto de corte.
Ahora une el punto B con el punto de fuga del lado izquierdo, y A con el punto de fuga del lado derecho. El punto donde se cortan ambas líneas es un punto que tiene una anchura de 7cm y una profundidad de 4cm. Si quisieras dibujar un rectángulo de 7x4cm, ésta sería su planta. Al punto de intersección llámalo AB. Ahora lo que tienes se debe parecer a ésto:
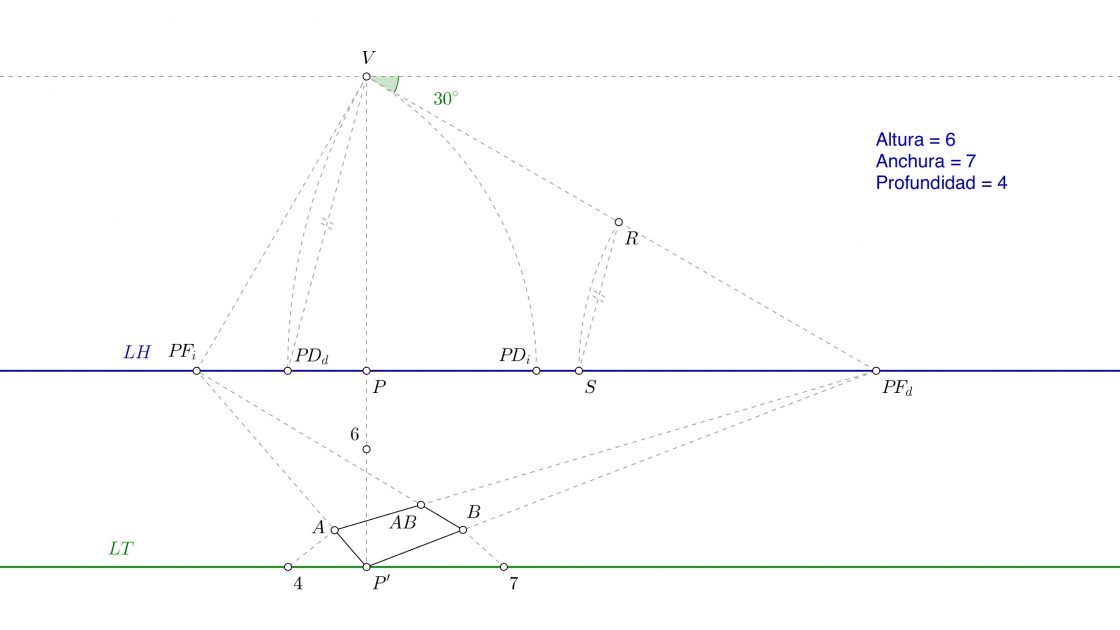
Tercer paso: Altura
Ahora ya solo queda marcar la altura para ver dónde se encuentra el punto en perspectiva. Lo primero que debes recordar es que las alturas que tomamos sobre la línea que va de P a P’ SOLO (y esto es muy importante) pueden cortar a las perpendiculares que nacen en las líneas que van de P’ a PFd o de P’ a PFi. En ninguna otra. Entonces… ¿Cómo medimos las alturas en otro punto? La respuesta es sencilla, mediante fugas. Primero debemos cortar a una de las perpendiculares que si podemos cortar. Puede ser la que sube por A, o la que sube por B. En este ejemplo yo marcaré la que pasa por B, pero lo puedes hacer con A y el resultado será el mismo.
Dibuja la línea que va desde la altura que marcaste hacia el punto de fuga del lado derecho. Ahora levanta una perpendicular que pase por B y mira donde te corta a la recta anterior. Ese punto será B6 (el punto B, pero a 6cm de altura). En la aplicación interactiva que tienes al final de ésta página lo he llamado BC.
Ahora une el punto B6 con el punto de fuga del lado izquierdo. Para terminar, levanta una perpendicular por el punto AB y comprueba donde corta a la línea anterior. Ese punto será el punto AB6 (abajo lo he llamado ABC). Es decir, el punto AB, pero a 6cm de altura. El resultado final es éste.
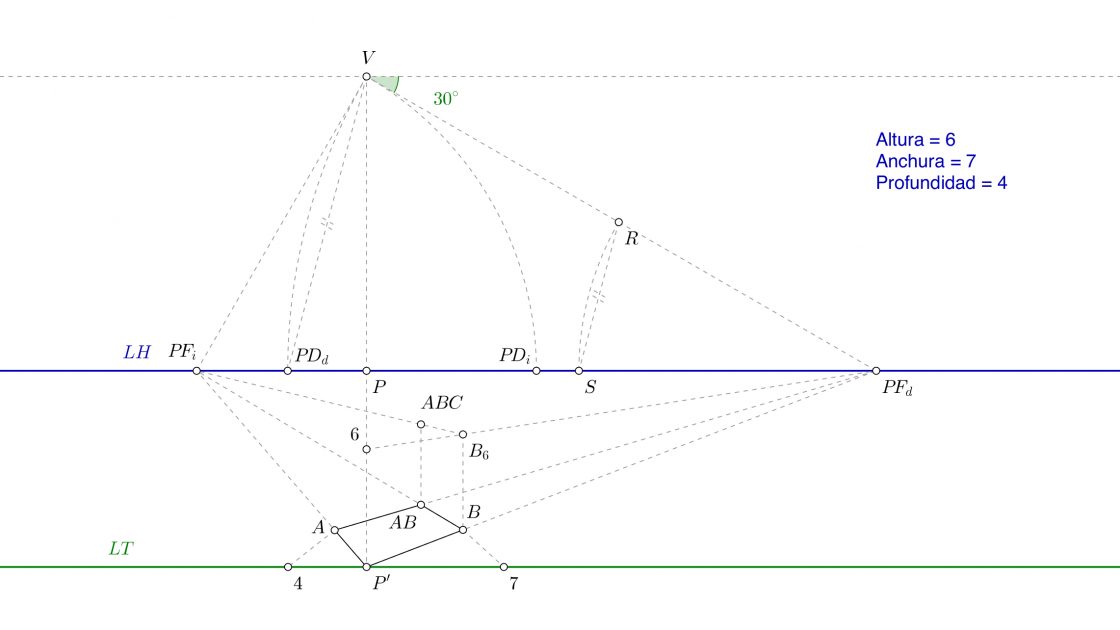
Explicación de la aplicación interactiva
Espero que todo lo anterior te haya aclarado las ideas. Para terminar te dejo aquí abajo una aplicación interactiva que creo que te puede ayudar a entenderlo un poco mejor si aún no lo comprendes. Puedes mover todos los puntos azules. De esa manera, puedes cambiar la Línea de Tierra, la Línea del Horizonte, el Punto de Vista y el Punto de Fuga Derecho. No puedes modificar los Puntos de Distancia ni el Punto de Fuga Izquierdo porque el programa los calcula de forma automática.
También puedes modificar los puntos A’, B’ y C’. Cada uno de estos puntos representa una de las tres dimensiones del punto. Así, A’ representa la profundidad. El punto B’ representa la anchura. Para terminar, C’ marca la altura a la que se encuentra el punto.
La figura que puedes ver a la derecha representa la planta de la figura, y su posición respecto al plano del cuadro. Puedes mover el punto O para situarlo donde puedas verlo mejor. Si quieres, puedes alejar o acercar la imagen con la rueda del ratón. O moverla pinchando sobre un espacio vacío y arrastrando. En caso de duda, aquí te dejo un vídeo explicando que es cada cosa para que lo veas en funcionamiento.
Vídeo aclaratorio a la aplicación interactiva
Aplicación interactiva
Aquí la tienes… ¡Disfruta!
Si encuentras cualquier fallo o error, por favor déjame un comentario o mándame un email para que la arregle.
