Perpendicularidad entre rectas y planos en sistema diédrico

Cuando hablamos de perpendicularidad en el sistema diédrico, nos referimos a la relación existente entre dos rectas, dos planos, o un plano y una recta. A continuación te explicaré los problemas más comunes que puedes llegar a encontrarte.

Perpendicularidad entre una recta y un plano

Cuando una recta es perpendicular a un plano, entonces será perpendicular a cualquier recta contenida en el mismo. Debes comprender que no estamos hablando de geometría plana, sino de sistemas de representación tridimensionales. Esto significa que para que dos rectas sean perpendiculares entre sí, no necesariamente deben cortarse. Aparte de eso, debido a la deformación que se sufre en las proyecciones en sistema diédrico, rara vez se puede apreciar la perpendicularidad en las proyecciones.

Así pues, para dibujar una recta perpendicular a otra, solo debes dibujar un plano perpendicular a dicha recta. Luego dibujar cualquier recta contenida en dicho plano. De ese modo determinas una recta perpendicular a la primera.

1. Marca un punto cualquiera sobre una de las proyecciones de la recta. En este caso puedes marcar un punto cualquiera sobre la proyección vertical de la recta. Llámalo A.
2. Dibuja una recta perpendicular a la proyección vertical de la recta que pase por A. Donde esa perpendicular corta a la línea de tierra tienes el punto B. Si unes B con A obtienes la traza vertical de un plano perpendicular a la recta original.
3. Continua trazando una recta perpendicular a la proyección horizontal de la recta que pase por B. Esa recta será la traza horizontal del plano perpendicular a la recta inicial.
4. Ahora solo debes dibujar una recta cualquiera contenida en ese plano. Para ello marca un punto cualquiera sobre una de las trazas. Por ejemplo D₂ sobre la traza vertical. Si realizas una perpendicular a la línea de tierra que pase por D₂ tienes la proyección horizontal del punto en la intersección con la línea de tierra. Ese punto llámalo D₁.
5. Luego marca otro punto cualquiera sobre la traza horizontal. A ese punto llámalo E₁. Si realizas una perpendicular a la línea de tierra que pase por E₁ tienes el punto E₂ en el punto de corte con la línea de tierra. Ese punto es la proyección vertical del punto E.
6. Uniendo por un lado D₂ con E₂, y por otro lado D₁ con E₁ tienes las proyecciones de la recta perpendicular a la que conocías al principio.

No creas que todos los problemas que te vas a encontrar son tan sencillos como este. Lo más habitual es que añadan algún requisito adicional para complicar el ejercicio. Así pues, los dos problemas más típicos serían los siguientes:

Trazar una recta perpendicular a un plano por un punto dado

Para este ejercicio te proporcionan las trazas de un plano y un punto cualquiera. Se te pide dibujar una recta perpendicular al plano. Lo más común es complicarlo transformándolo en un ejercicio de intersecciones de rectas y planos en sistema diédrico. Tu punto de partida será pues algo similar al siguiente.

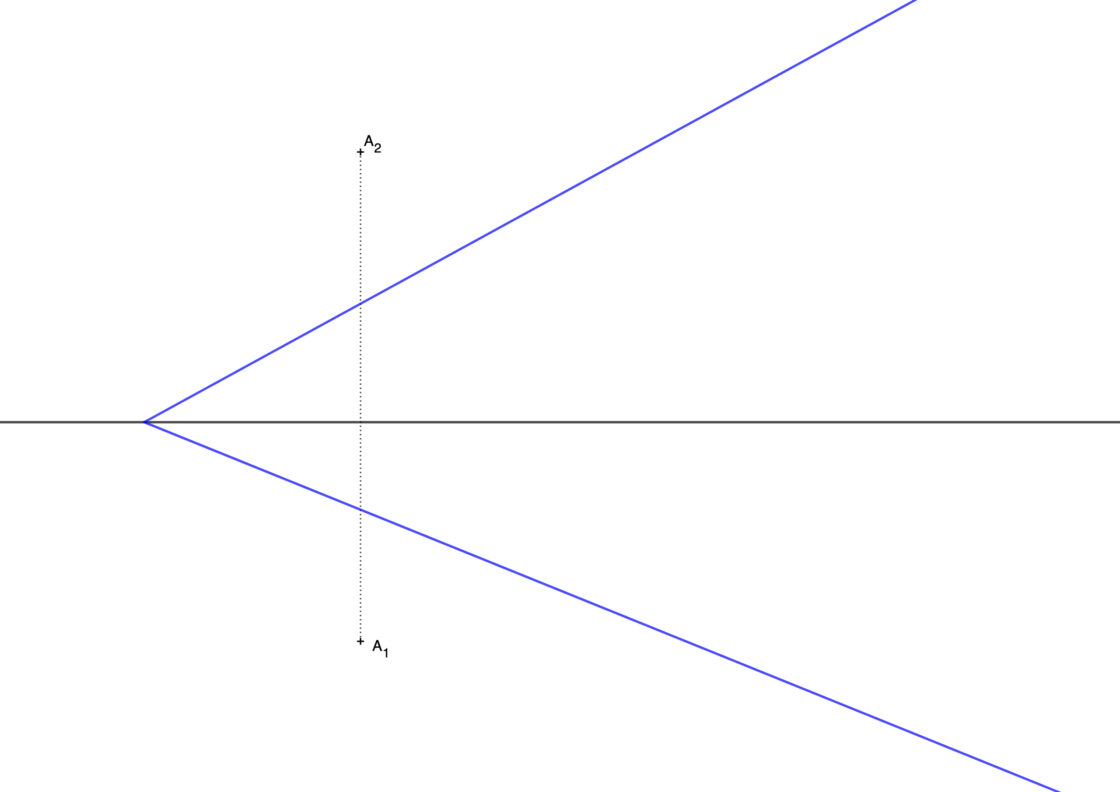
1. Empieza dibujando una recta perpendicular a la traza vertical del plano que pase por A₂. Esa será la proyección vertical de la recta perpendicular al plano.
2. Ahora dibuja una recta perpendicular a la traza horizontal del plano que pase por A₁. De esa manera estás dibujando la proyección horizontal de la recta perpendicular.

La parte más complicada vendría después. Si no te piden nada más solo tienes que hallar el lugar donde la recta corta a los planos proyectantes para ver donde dejamos de ver la recta. Un truco es ver que proyección llega antes a la línea de tierra. En caso de que la proyección horizontal llegue antes, significa que la traza se encuentra sobre el plano vertical. Pero si la proyección vertical llega antes, entonces la traza está sobre el plano horizontal. Aquí abajo puedes ver que la proyección horizontal llega antes, por lo que corta sobre el plano vertical. Pero puedes mover los puntos para cambiar la posición y ver como funciona.

Dibujar un plano perpendicular a una recta que pase por un punto en sistema diédrico

Para este ejercicio conoces las proyecciones horizontal y vertical de una recta. También conoces un punto concreto A representado por sus proyecciones A₂ y A₁. Así pues, tu punto de partida será algo similar a la imagen que ves a continuación.

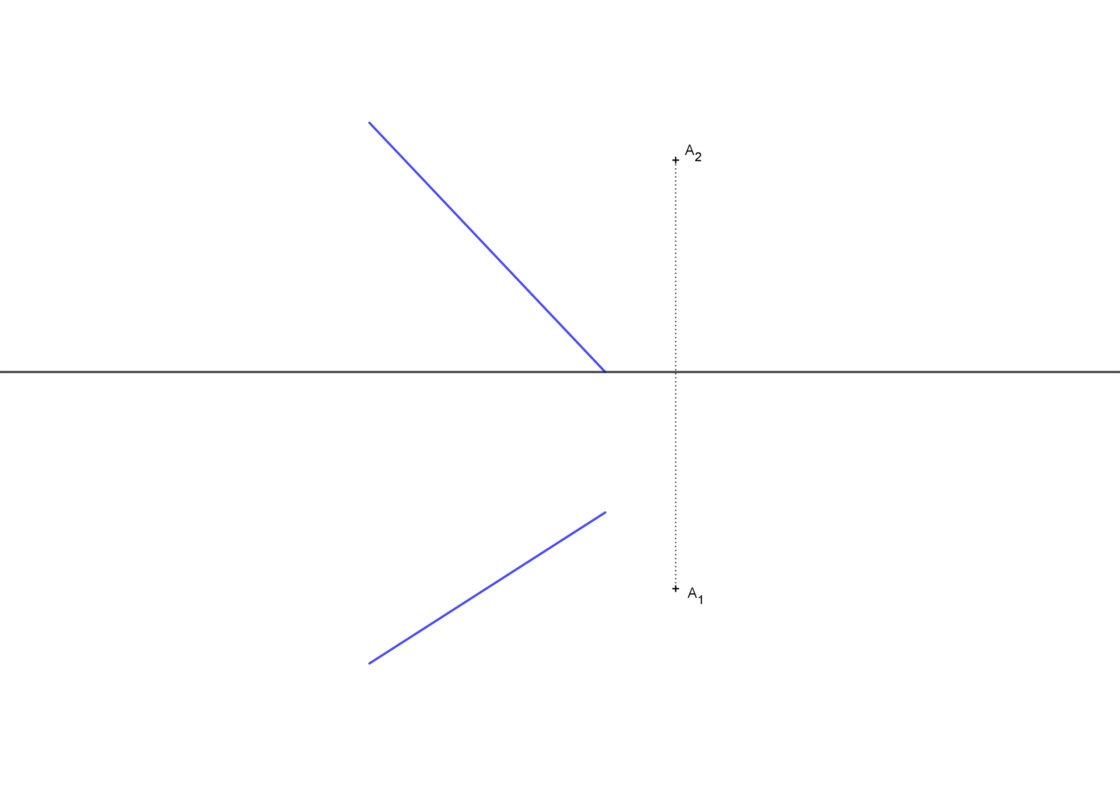
1. Empieza dibujando una recta horizontal contenida en el plano que quieres dibujar. Para ello dibuja una recta paralela a la línea de tierra que pase por A₂.
2. Ahora dibuja una línea perpendicular a la proyección horizontal de la recta que pase por A₁. Donde esa perpendicular corta a la línea de tierra tienes el punto B₁, que es la proyección horizontal de la traza de la recta horizontal contenida en el plano que buscas.
3. Traza una perpendicular a la línea de tierra que pase por B₁. Donde esa perpendicular corta a la recta paralela que dibujaste en el primer paso tienes el punto B₂, que representa la traza de la recta horizontal contenida en el plano. Por tanto, el punto B₂ se encuentra en la traza del plano que buscas.
4. Dibuja una línea perpendicular a la proyección vertical de la recta que pase por B₂. Esa es la traza vertical del plano que buscas. Donde esa traza corta a la línea de tierra tienes el punto C, común a ambas trazas del plano.
5. Para terminar, dibuja una línea perpendicular a la proyección horizontal de la recta que pase por el punto C. Esa será la traza horizontal del plano.