La intersección entre dos planos es una recta. Para hallar las proyecciones de dicha recta tan solo tienes que unir los puntos donde se cortan las trazas de ambos planos. Aquí abajo tienes un ejemplo interactivo que espero que te ayude a comprender este concepto.
Ejercicio sencillo de intersección de planos en diédrico
Para practicar esto te propongo un ejercicio muy sencillo y muy básico de intersección de planos. Dibuja una línea horizontal que representará la línea de tierra. Sobre ella marca dos puntos, A y B, que serán los puntos de corte de dos planos con la línea de tierra. Luego traza dos líneas que partan de A, y otras dos que partan de B. Esas cuatro líneas son las trazas de ambos planos con los planos horizontal y vertical.
- El punto donde las dos trazas horizontales se cortan es D1. Date cuenta de que al cortarse en el plano horizontal, ese punto no tiene altura. Por tanto el punto D2 se encuentra sobre la línea de tierra.
- Donde las dos trazas verticales de los planos se cortan tienes el punto C2. Como ese punto se encuentra sobre el plano vertical, no tiene alejamiento, por tanto el punto C1 se encuentra sobre la línea de tierra.
- Si unes C2 con D2 tienes la proyección vertical de la recta que es la intersección de ambos planos.
- La proyección horizontal de la intersección de ambos planos la obtienes uniendo C1 con D1.
Intersección de rectas en sistema diédrico
La intersección de dos rectas en sistema diédrico es siempre un punto. Date cuenta de que para que dos rectas se corten, la intersección de las proyecciones de ambas rectas se deben encontrar sobre la misma perpendicular a la línea de tierra. De lo contrario no habrá un punto de corte.
En la aplicación de aquí abajo puedes mover los puntos azules para modificar las rectas. Las proyecciones en diédrico se calcularán de forma automática. Date cuenta de que para que las dos rectas se corten, la intersección de las proyecciones debe representar un único punto tanto sobre el plano vertical como sobre el horizontal.
Intersección de rectas y planos en sistema diédrico
Ahora que ya sabes los conceptos básicos, te voy a explicar como realizar la intersección de una recta y un plano. El truco consiste en dibujar un plano que contenga a la recta. Lo más sencillo es usar un plano proyectante, ya sea vertical u horizontal. Te lo voy a explicar con un ejemplo. A continuación tienes la intersección del plano que forman ABC con la recta determinada por O y P. ¿Dónde se cortan?
Así a simple vista no es fácil de interpretar. Antes te he explicado como hacer la intersección de dos planos. ¿Y si en vez de una recta y un plano fuera la intersección de dos planos? Mucho más fácil, ¿verdad? Pues el truco es ese, incluye la recta que forman O y P en un plano. De esa manera el ejercicio se transforma en lo que ves a continuación.
Ahora el problema es mucho más sencillo. Todo lo que tienes que hacer es calcular la intersección de esos dos planos. El lugar donde esa intersección coincide con la recta es donde la recta corta al plano.
Ejercicio resuelto de intersección de una recta y un plano en diédrico
Ahora te toca practicar. A continuación tienes un ejercicio muy típico de este tipo de problemas. Se te proporciona una recta, representada por sus proyecciones, y un plano, representado por sus trazas. Tu punto de partida será algo parecido a esto.
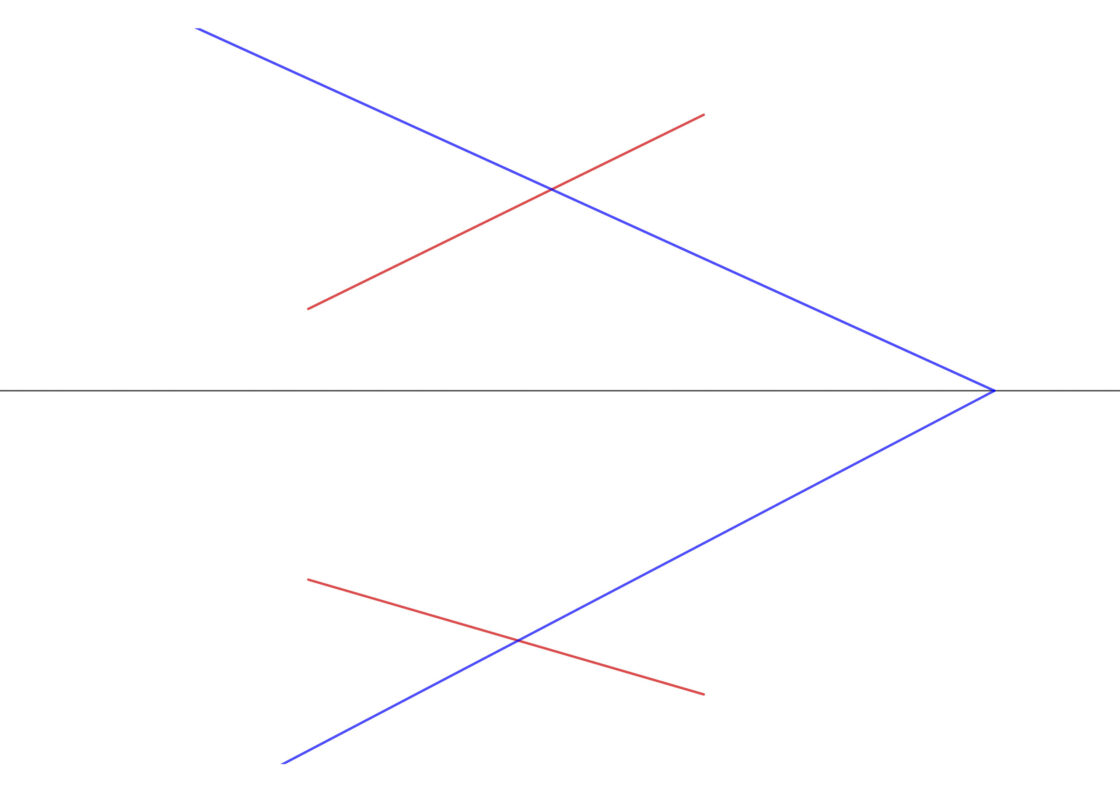
Puedes pulsar sobre la imagen de aquí arriba para abrirla en una nueva ventana y así imprimirla en un A4 para practicar.
- Para resolverlo empieza por dibujar un plano proyectante vertical que contenga a la recta. Por tanto debes prolongar la proyección vertical de la recta, donde corta a la línea de tierra tienes el punto D2.
- Dibuja una perpendicular a la línea de tierra que pase por D2. Donde esa perpendicular corta a la traza horizontal del plano tienes el punto D1. Ese punto es la intersección de la traza horizontal del plano proyectante con la traza horizontal del plano que conoces.
- Comprueba donde corta la proyección vertical de la recta (ahora se transforma en la traza vertical del plano proyectante) a la traza del plano que conoces. Ese punto es C2, la intersección de las trazas verticales de los planos.
- Traza una perpendicular a la línea de tierra que pase por C2. Donde esa perpendicular corta a la línea de tierra tienes el punto C1.
- Une D1 con C1 con una línea. Donde esa línea corta a la proyección horizontal del plano tienes el punto P1. Ese punto es la proyección horizontal de la intersección de la recta y el plano.
- Para terminar, dibuja una perpendicular a la línea de tierra que pase por P1. Donde esa perpendicular corta a la proyección vertical de la recta tienes P2.
- El punto P, representado por sus proyecciones vertical P2 y horizontal P1 es la intersección de la recta y el plano.
