Perpendicularidad entre rectas en sistema diédrico

Hay un concepto que debes tener en cuenta cuando hablamos de perpendicularidad entre rectas en sistema diédrico. Date cuenta de que dos rectas perpendiculares en el espacio no tienen porqué tener sus proyecciones perpendiculares en sus proyecciones sobre los planos proyectantes en diédrico. Bueno, hay una excepción. Cuando se cumple el Teorema de las tres perpendiculares si que son perpendiculares entre si. Si te estás preguntando que es eso del Teorema de las tres perpendiculares, te lo explicaré. Este teorema dice que:

«Si por el pie de una perpendicular r a un plano trazamos una recta perpendicular s a una recta t contenida en el plano, todo segmento que una el punto de intersección de estas dos últimas (s y t) con un punto P cualquiera de la perpendicular al plano será perpendicular a la recta contenida en el plano.»

De la misma manera, si las proyecciones ortogonales son perpendiculares y una de ellas es paralela o pertenece al plano, entonces las rectas también son perpendiculares en el espacio. Los ejercicios más comunes que te puedes encontrar sobre este tipo de problemas suelen pedirte que una recta sea perpendicular a otra y que pase por un punto concreto.

Recta perpendicular a r que pasa por A

Como te decía antes, en este tipo de ejercicios conoces una recta determinada r. Esta recta la definen sus proyecciones horizontal y vertical r₁ y r₂. También conoces un punto del plano A determinado por las proyecciones vertical y horizontal A₁ y A₂.

El proceso para resolver este ejercicio es el siguiente: Primero dibujas un plano perpendicular a la recta r que pase por A. Luego calculas la intersección de ese plano con la recta r. Para terminar solo tienes que unir ese punto de intersección con el punto A.

Una versión simplificada de esto en tridimensional sería algo parecido a lo siguiente. La pega es que las rectas y planos casi siempre son oblicuos en diédrico.

Este ejercicio es bastante complejo, ya que para poder realizarlo correctamente necesitas saber realizar varios procedimientos previos. En primer lugar necesitas saber cómo dibujar un plano perpendicular a una recta que pasa por un punto. También necesitas saber cómo hallar la intersección entre una recta y un plano. Tu punto de partida será algo parecido a esto:

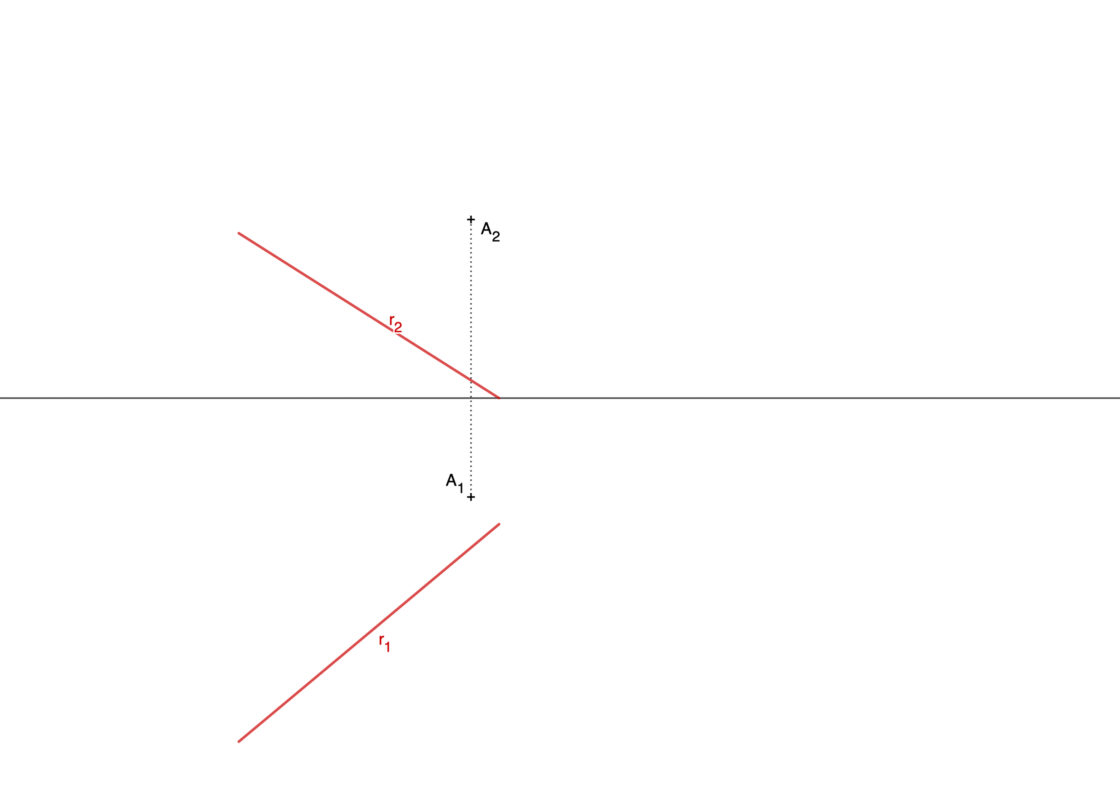
1. El primer paso será dibujar un plano perpendicular a la recta y que pase por A. Para ello primero debes dibujar una recta frontal que esté contenida en el plano y que pase por A. Así pues, dibuja una línea perpendicular a la traza vertical de la recta y que pase por A₂. Donde esa recta corta a la línea de tierra tienes el punto B₂.
2. Ahora dibuja una recta paralela a la línea de tierra que pase por A₁. Sobre esa línea tendrás la proyección horizontal de la recta frontal. Dibuja una perpendicular a la línea de tierra que pase por B₂. Donde esa perpendicular corta a la paralela que pasa por A₁ tienes B₁, que es la traza horizontal de la recta frontal. Date cuenta de que B₁ se encuentra sobre la traza horizontal del plano perpendicular.
3. Traza una perpendicular a la proyección horizontal r₁ de la recta original y que pase por B₁. Esa es la traza horizontal del plano vertical. Donde esa recta corta a la línea de tierra tienes el punto C.
4. Dibuja una recta perpendicular a la proyección vertical r₂ de la recta. Esa es la traza vertical del plano perpendicular. Ahora que ya conoces el plano perpendicular a la recta original, el siguiente paso será hallar la intersección con esa recta. Para ello recuerda que debes dibujar un plano proyectante vertical que contenga a la recta.
5. Las trazas de ese plano proyectante serán la proyección vertical r₂ de la recta, y una recta perpendicular a la línea de tierra que parta desde el punto de intersección de esa proyección con la línea de tierra. En este caso ese punto equivale tanto a F₂ como a H₁. Ten en cuenta que se superponen.
6. Ahora debes hallar la intersección de esos dos planos, el proyectante vertical y el perpendicular a la recta. El punto donde ambas trazas verticales se cortan es el punto D₂. Dibuja una perpendicular a la línea de tierra por ese punto para hallar la proyección horizontal del mismo, que puedes llamar D₁.
7. Donde las trazas horizontales de ambos planos se cortan tienes el punto H₁. La recta que va de D a H es la intersección de ambos planos. En diédrico se representa uniendo D₂ con H₂ por un lado, y D₁ con H₁ por el otro. Donde esa línea corta a la original tienes el punto I. En este caso la línea que va de D₂ a H₂ corta a la proyección vertical r₂ de la recta en el punto I₂.
8. Por otra parte, la línea que va de D₁ a H₁ cortará a la proyección horizontal r₁ de la recta original en el punto I₁.
9. La recta que estás buscando la obtienes uniendo I₂ con A₂ por un lado, y A₁ con I₁ por el otro.
10. Para terminar, los puntos J y K determinan las trazas de esa recta sobre los planos proyectantes.

Te recomiendo ponerlo a pantalla completa y hacer zoom sobre las distintas zonas para poder ver el resultado, ya que son muchos puntos y líneas todos juntos.