Enlaces de arcos y circunferencias

Los enlaces están muy relacionados con el tema de las tangencias. Ten en cuenta que en realidad se trata de realizar circunferencias tangentes, pero sin llegar a dibujarlas enteras, tan solo se dibujan arcos.

Enlace de varios puntos

En éste tipo de ejercicios los datos que conoces son un arco inicial, representado por A y B, así como el centro de la circunferencia que contiene ese arco. Se te pide realizar el enlace de los puntos B, C, D y E. Para resolver este ejercicio debes recordar dos propiedades de las tangencias. La primera, que los centros de dos circunferencias tangentes están alineados con el punto de tangencia. En este caso, los distintos puntos A, B, C, D… representan los puntos de tangencia. Lo segundo que debes recordar es que en cualquier circunferencia, la mediatriz de cualquier cuerda siempre pasa por el centro. Como puedes comprobar, los distintos puntos se encuentran en las circunferencias tangentes, por tanto forman cuerdas.

Tu punto de partida será algo parecido a la imagen siguiente:

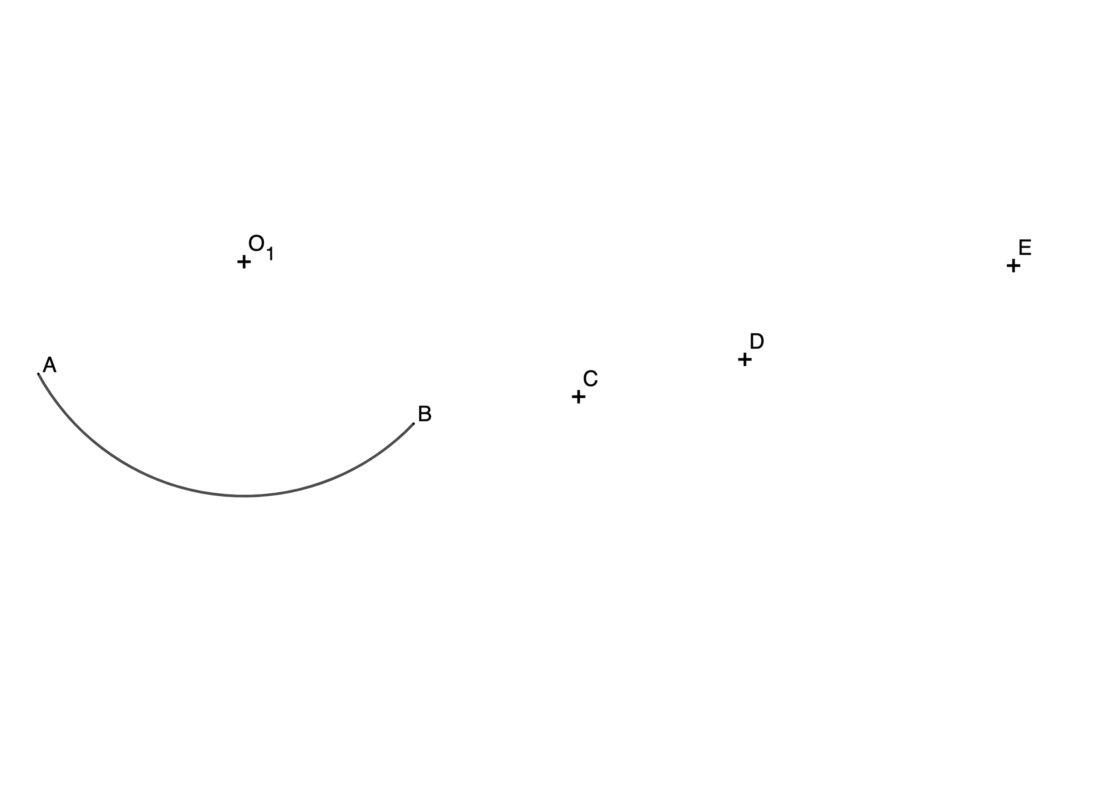
El punto de partida sería algo parecido a la imagen que tienes aquí arriba. Puedes descargarla pulsando sobre el botón derecho o bien pulsar sobre ella e imprimirla en una impresora doméstica en formato DIN A4. De ese modo tendrás un ejercicio de muestra para practicar. Si tratas de poner los puntos al azar es muy fácil que alguno de los centros salga fuera del plano.

Sabiendo esto, te explico paso a paso como resolverlo y el porqué de la misma.

1. Empieza por dibujar la línea que une O₁ con B y prolóngalo. El centro de la siguiente circunferencia tangente debe estar alineado con O₁ y B.
2. Los puntos B y C forman una cuerda de la circunferencia de centro O₂. Es decir el centro O₂ que todavía no conoces debe estar sobre la mediatriz del segmento BC. Así pues, dibuja esa mediatriz.
3. El punto del plano donde se cruza la recta que pasa por O₁ y B con la mediatriz del segmento BC es el único punto del plano donde se cumplen ambas propiedades. Por tanto, es el centro O₂ de la segunda circunferencia.
4. Para hallar los demás centros solo tienes que repetir el proceso varias veces. Dibuja la línea que pasa por O₂ y C.
5. Halla la mediatriz de C y D para ver donde corta a la recta anterior. Ese punto es O₃.
6. Une O₃ con D y prolóngalo. Donde corta a la mediatriz de D y E tienes el centro O₄.
7. Para terminar, con centro en O₂ y radio hasta B, dibuja un arco. Luego dibuja otro con centro en O₃ y radio hasta C. El último arco será el de centro O₄ y radio hasta D.

Aquí abajo tienes un vídeo explicativo donde puedes ver el proceso completo.

Enlace de arcos (cóncavo)

Este tipo de ejercicios te proporcionan dos arcos y el radio de la solución. Para resolverlo deberás dibujar el arco que enlace a los dos arcos iniciales y que esté contenido en una circunferencia de radio igual al de la solución proporcionada. Este ejercicio se resuelve de la misma manera que cuando te piden dibujar circunferencias tangentes a otras dos circunferencias conociendo el radio. Al decir cóncavo se refiere a que el radio de la solución es pequeño y no puede contener a ninguna de las dos circunferencias iniciales. Tu punto de partida se parecerá a esto, si lo imprimes en un A4, aplica radio 5cm para la solución. En caso de que sea una cuartilla, usa radio 2cm.

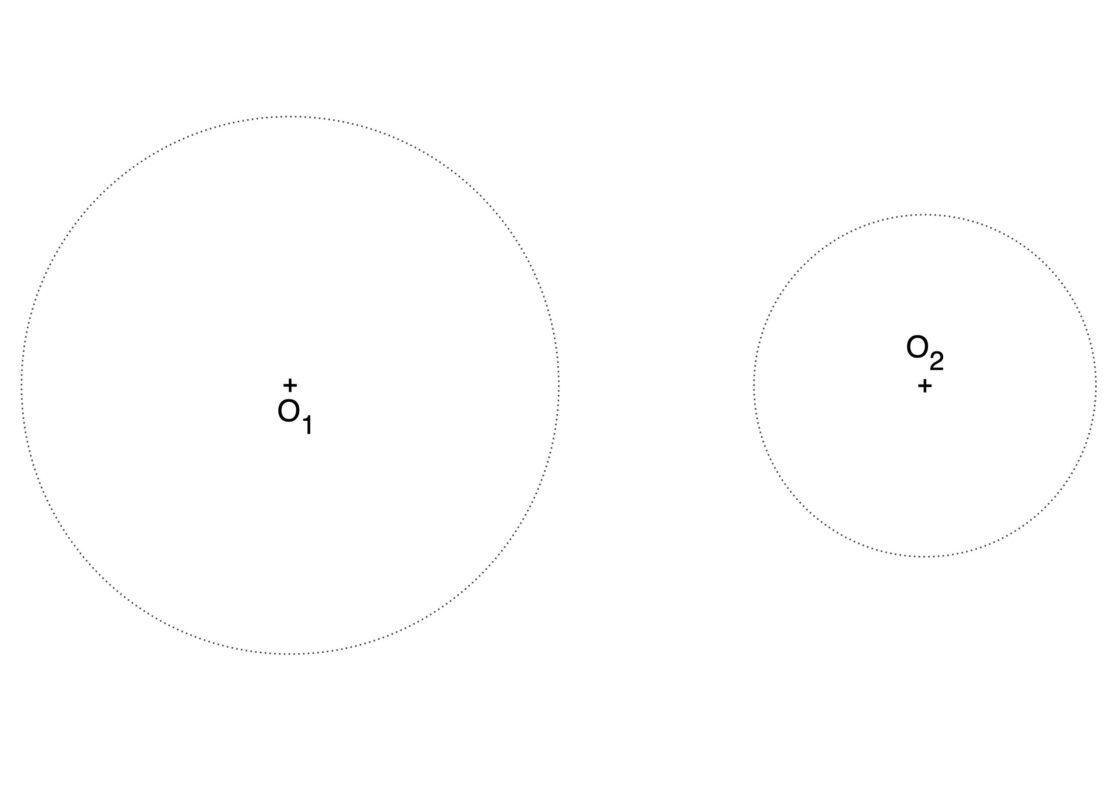
1. Dibuja una semirrecta cualquiera con inicio en O₁. El punto donde corta al arco llámalo S.
2. Sobre esa misma semirrecta, a continuación de S marca la longitud del radio de la solución que te dan en el enunciado. De esa forma obtienes el punto T.
3. Con centro en O₁ y radio O₁T dibuja un arco.
4. Ahora tienes que repetir todos esos pasos desde el centro O₂.
5. Traza una línea que pase por O₂. Al punto donde esa línea corta al arco llámalo P.
6. En esa línea, a continuación de P, mide la longitud del radio de la solución. A ese punto llámalo R.
7. Dibuja un arco con centro en O₂ y radio hasta R.
8. Donde esos arcos se cortan tienes O₃, centro del arco que buscas.
9. Si unes O₃ con O₂ con una línea por un lado, y O₃ con O₁ por el otro, tienes los puntos T₁ y T₂ de tangencia donde cortan a ambos arcos.
10. Para terminar, con centro en O₃ y radio hasta T₁ dibuja un arco que vaya de T₁ a T₂. Esa es la solución que buscas.

Y aquí abajo tienes un vídeo explicativo por si te queda alguna duda, para que lo puedas repasar.

Enlaces de arcos de circunferencia (convexo)

Para resolver este tipo de problemas te proporcionan los dos arcos iniciales, así como el radio de la solución. En ésta ocasión el radio es tan grande que contiene a las circunferencias que contienen los dos arcos iniciales. Este ejercicio es similar al anterior. La diferencia radica en que en esta ocasión el radio de la solución es tan grande que abarca a ambas circunferencias. Por lo tanto la solución se haya restando radios en vez de sumándolos. Tu punto de partida se parece a esto, si lo imprimes en una cuartilla, el radio de la solución será de 7cm. Si lo imprimes en A4, considera 15cm.

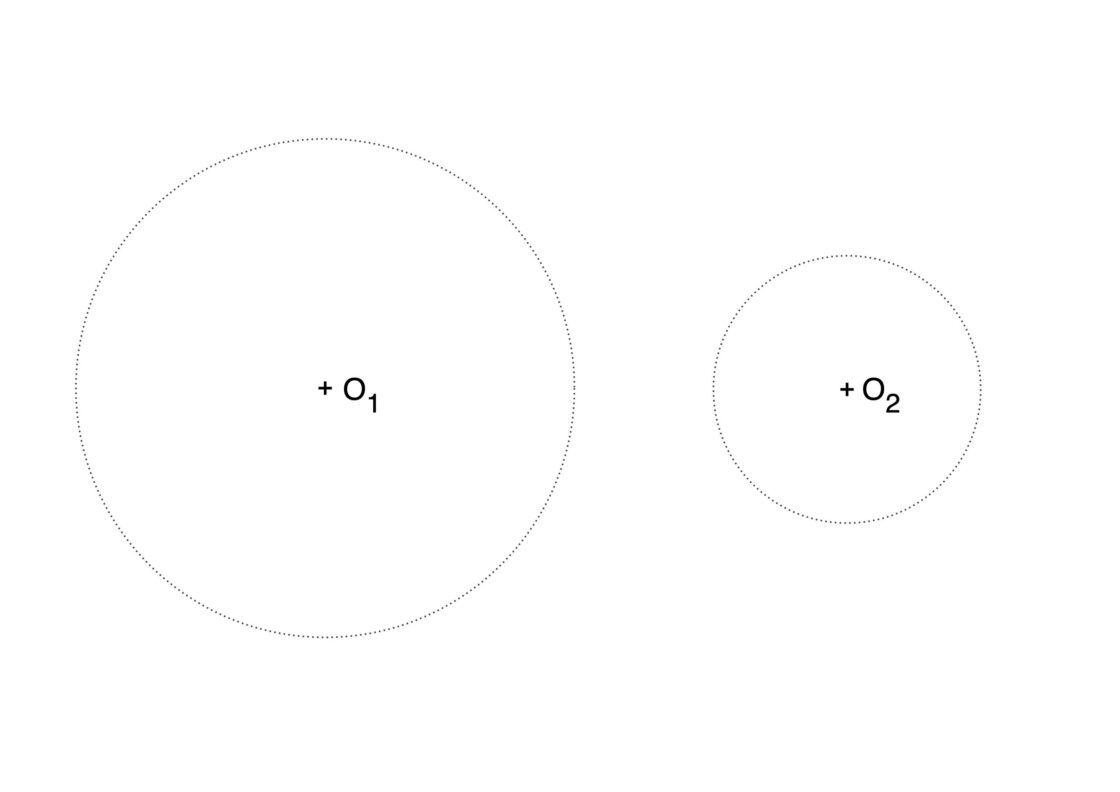
1. Marca un punto cualquiera del primer arco, de centro O₁ y llámalo P.
2. Dibuja una línea que pase por P y por el centro O₁ de ese arco. Sobre esa línea, desde P, debes medir la distancia del radio que te proporcionan. De esa manera hallas el punto R.
3. Con centro en O₁ y radio hasta R dibuja un arco.
4. Ahora debes hacer exactamente lo mismo con el arco de centro O₂. Marca un punto cualquiera del arco al que llamarás S.
5. Traza una línea que pase por S y por O₂.
6. Sobre esa línea, a partir de S, marca la distancia del radio de la solución. Así obtienes el punto T.
7. Con el compás, dibuja un arco con centro en O₂ y radio hasta T.
8. Donde este arco corta con el que pasaba por R tienes el centro O₃.
9. Para hallar los puntos de tangencia, donde todos los arcos cambian de radio, dibuja líneas que pasen por O₁ y O₃ por un lado y por O₂ y O₃ por el otro. Donde esas líneas cortan a los arcos iniciales tienes T₁ y T₂, puntos de tangencia.
10. Ya para terminar, con centro en O₃ y radio hasta T₁ dibuja un arco que vaya de T₁ a T₂. Esa es la solución que buscas.

Al igual que pasaba con las circunferencias tangentes, este ejercicio presenta varias opciones. Te puedes encontrar que te pidan que incluya a una y no a la otra, por ejemplo. En tal caso, lo solucionarás mezclando este ejercicio con el anterior. Por uno de los centros sumarás el radio de la solución, mientras que por el otro lo restarás.

A continuación tienes un video en el que puedes ver como se resuelve este ejercicio paso a paso.

Enlace de dos arcos de circunferencia con dos arcos iguales y opuestos

Para resolver este ejercicio los elementos que conoces son dos arcos, y los dos puntos de tangencia que se deben enlazar. Los distintos ejercicios que puedes tener serían dos, o bien se pide enlazar con dos arcos iguales, o se pide enlazar con dos arcos distintos conociendo el radio de uno de ellos. En ambos casos vamos a partir de un inicio similar, parecido a esto:

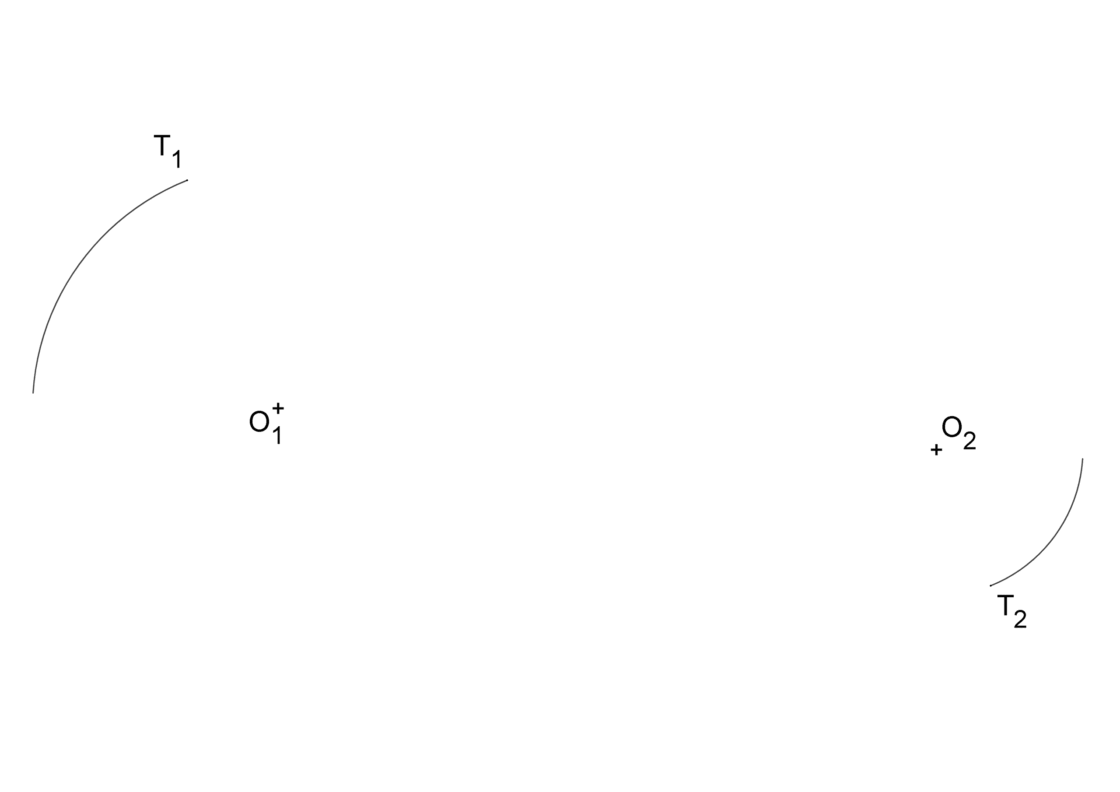
Enlazar con dos arcos iguales y opuestos

1. Dibuja la línea que une los dos puntos de tangencia y halla su punto medio, al que llamaremos T. Para ello necesitarás trazar la mediatriz de ese segmento.
2. Marca las mediatrices de T₁T y de T₂T
3. Traza las líneas que unen los puntos de tangencia con sus respectivos centros, donde esas líneas cortan a las mediatrices de antes tienes los centros O₃ y O₄
4. Con centro en O3 y O4 y radio hasta T puedes dibujar los dos arcos solución.

Enlace de dos arcos con dos arcos distintos, conociendo el radio de uno de ellos

El punto de partida es el mismo que antes, pero lo que se pide es un poco diferente. Supongamos que te piden que el arco tangente en T₁ mida un valor determinado al que llamaremos r₁.

1. Traza la línea que une T₁ con O₁ y sobre ella lleva la medida de r₁ para hallar O₃
2. Con centro en O₃ y radio hasta T₁ traza el primer arco, sobre la línea que une T₁ con T₂ tendrás el punto T donde debes cambiar el tamaño del arco.
3. Dibuja una línea que una T₂ con O₂ y prolóngala un poco.
4. Realiza la mediatriz de T₂T hasta cortar con la recta anterior. El punto de corte es O₄
5. Con centro en O₄ y radio hasta T puedes dibujar el arco que te falta para terminar el ejercicio.

Ayúdame a mejorar esta entrada

¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti.

«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.