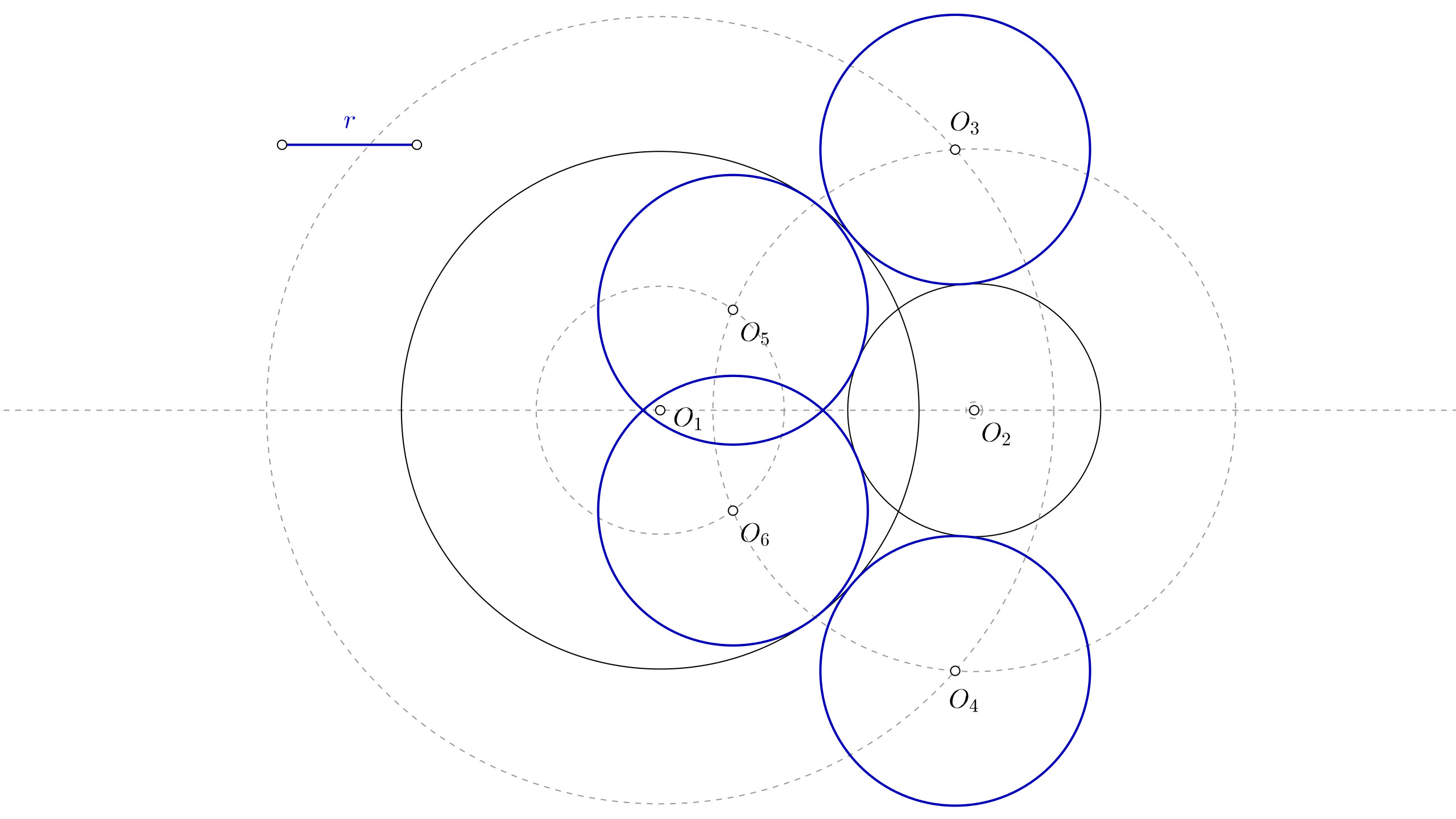
La resolución de circunferencias tangentes conocido el radio es relativamente sencillo. Todos estos ejercicios se basan en las propiedades de las tangencias. Vamos a ver los más habituales en geometría.
Circunferencias tangentes a una circunferencia que pasan por un punto exterior
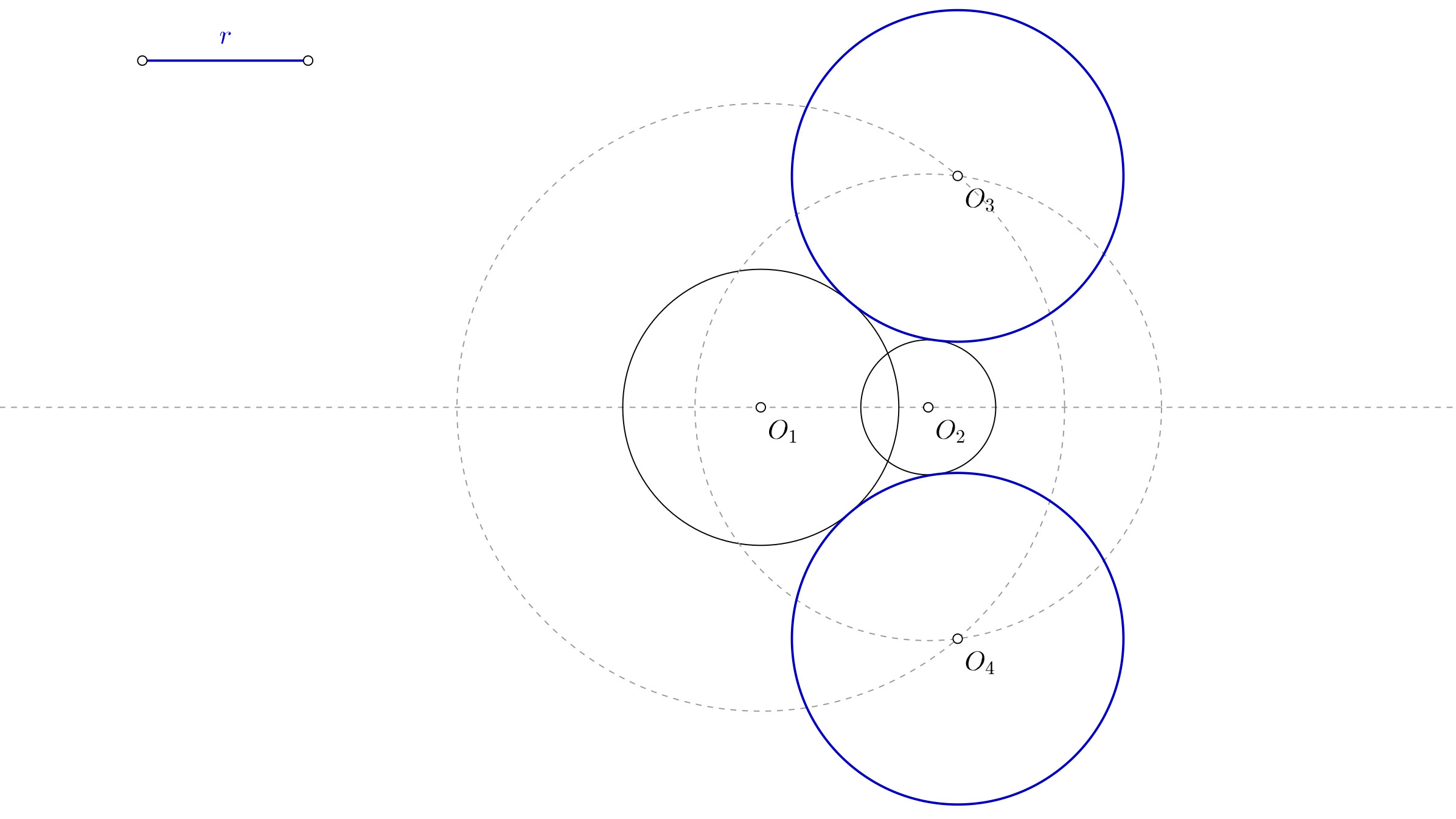
En este caso se te pide dibujar las circunferencias tangentes a una circunferencia y que pasan por un punto exterior a la misma. Por supuesto, conociendo el radio de la solución. Tu punto de partida se parece a esto:
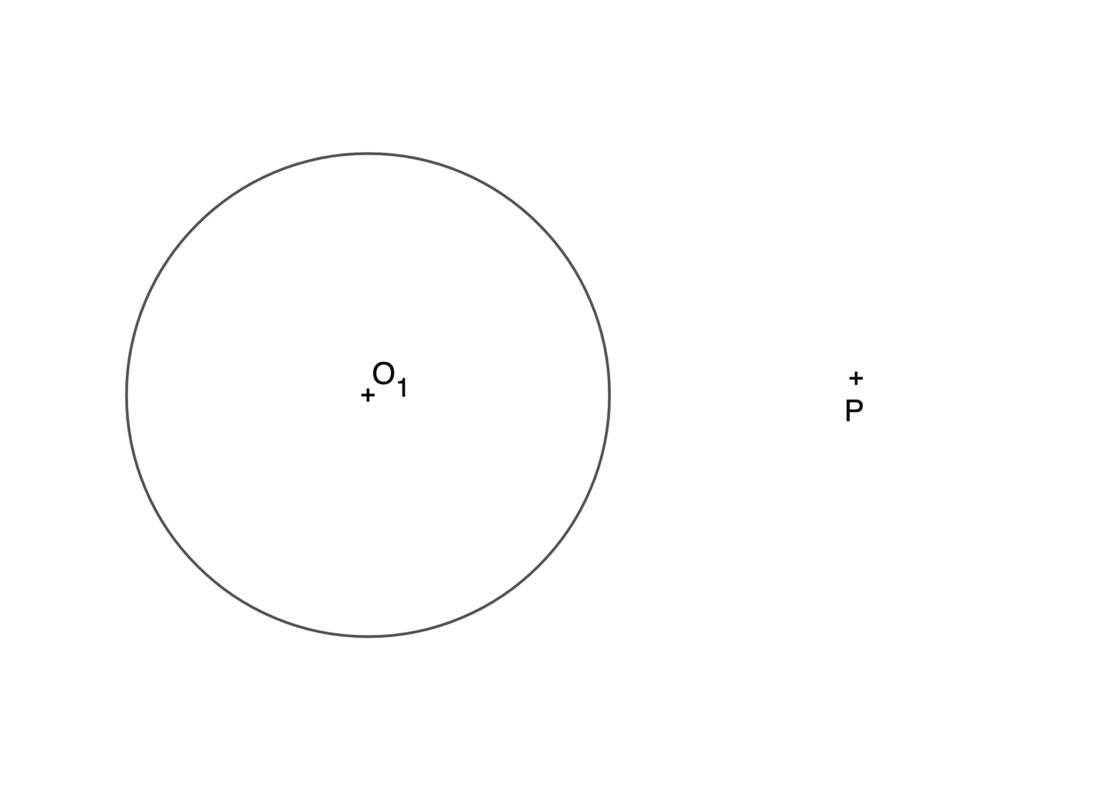
- Dibuja una línea cualquiera que pase por el centro de la circunferencia de centro O1 y prolóngalo. Donde esa línea corta a la circunferencia tienes el punto A.
- Sobre la prolongación de esa línea lleva la medida del radio a continuación. De esa manera obtienes el punto B.
- Con centro en O1 y radio hasta B traza una circunferencia.
- Ahora dibuja una circunferencia con centro en P y radio igual al de la solución que conoces. Donde esa circunferencia corta a la que dibujaste en el paso 3 tienes los puntos O2 y O3, centros de las circunferencias que buscas.
- Para terminar, dibuja sendas circunferencias con centro en O2 y O3 con el radio que te han proporcionado en el enunciado.
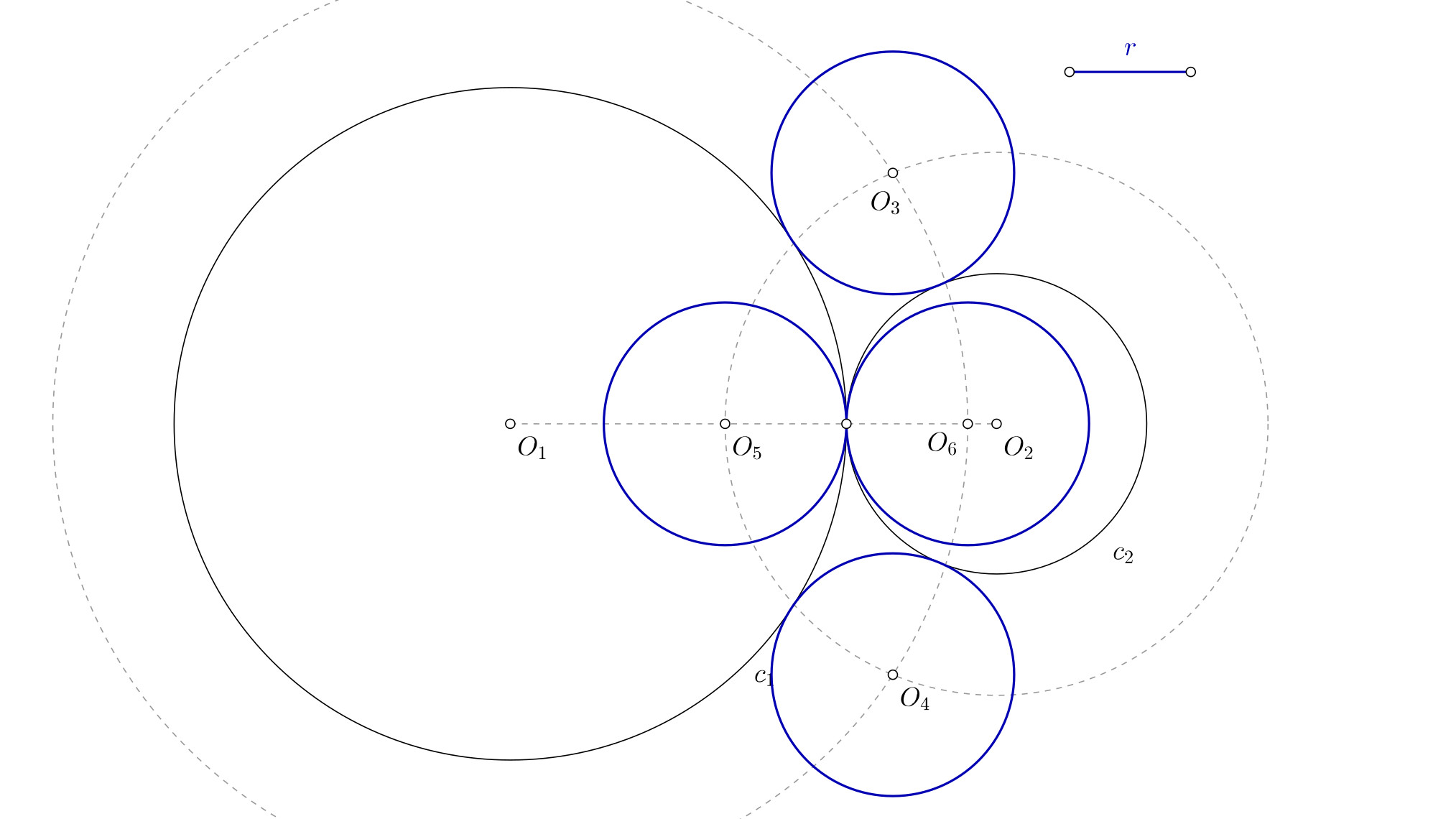
Caso particular: 4 circunferencias solución
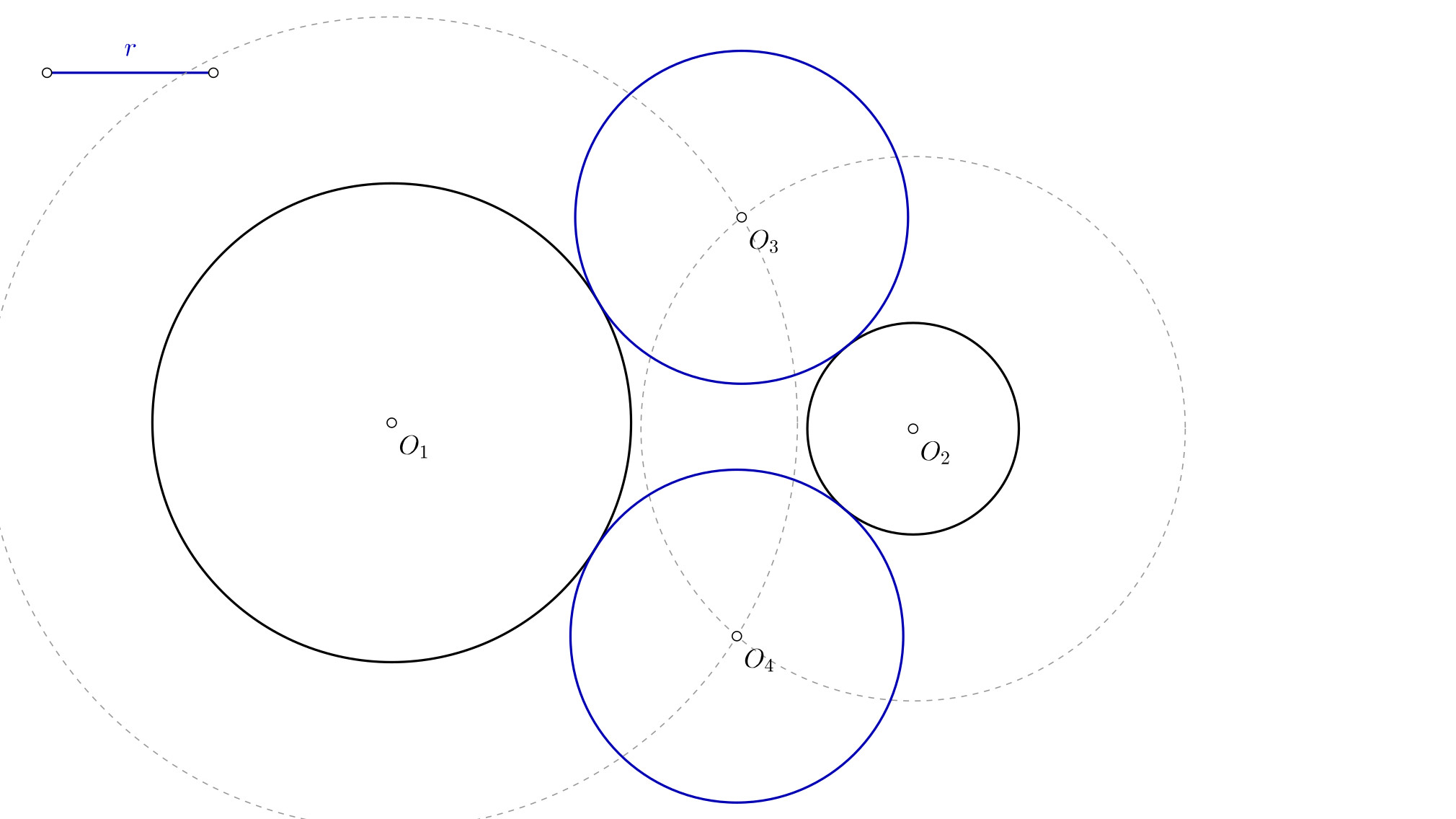
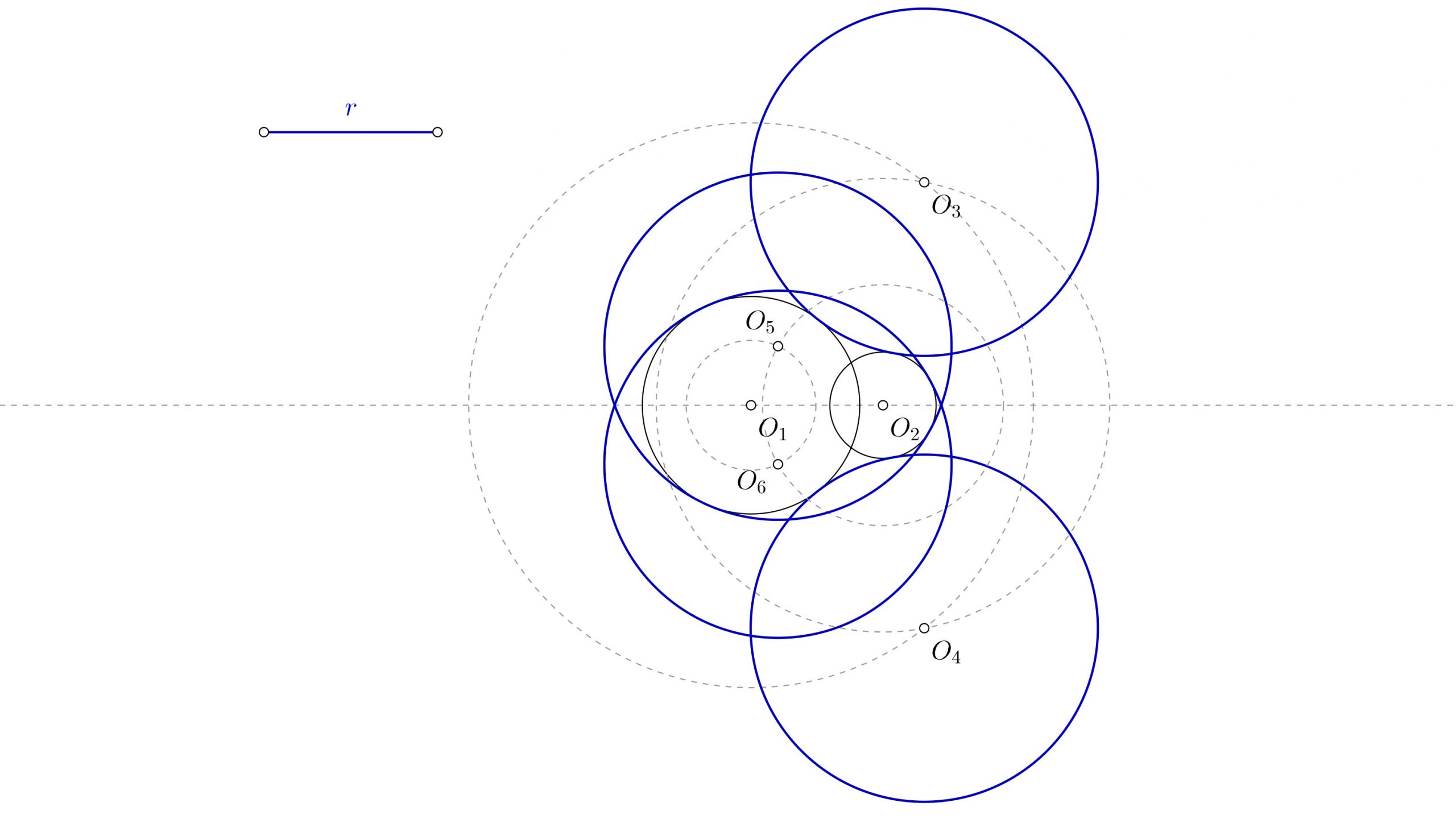
Este ejercicio tiene un caso particular que es interesante. En ocasiones puede ocurrir que el radio de la solución sea tan grande que englobe a la circunferencia inicial. En tal caso tendrás cuatro soluciones posibles. Dos de ellas estarán fuera (son las que has hallado antes) y otras dos que contendrán a la circunferencia inicial. Como ya has hallado las exteriores en el paso anterior, a continuación te explico como hallar las que contienen a la circunferencia inicial.
- Desde el punto A, lleva la medida del radio de la solución. Pero en esta ocasión, en vez de medir hacia afuera, mide hacia dentro de la circunferencia inicial. De ese modo obtienes el punto C.
- Con centro en O1 y radio O1C dibuja una circunferencia.
- Si no habías dibujado antes la circunferencia de centro P y radio igual al de la solución, dibújala ahora. Donde esa circunferencia corta a la que dibujaste en el paso 2 tienes los centros O4 y O5.
- Dibuja las dos circunferencias que te faltan. Con el compás, con centro en O4 y O5 y radio igual a la solución que conoces.
Circunferencias tangentes a dos rectas que se cortan
Los datos que conoces son dos rectas iniciales t y s que se cortan, y el radio de las circunferencias que debes hallar. Ten en cuenta que para la correcta resolución de éste ejercicio deberás dibujar cuatro circunferencias distintas, una para cada sector que determinan las rectas. Tu punto de partida será semejante a esto:
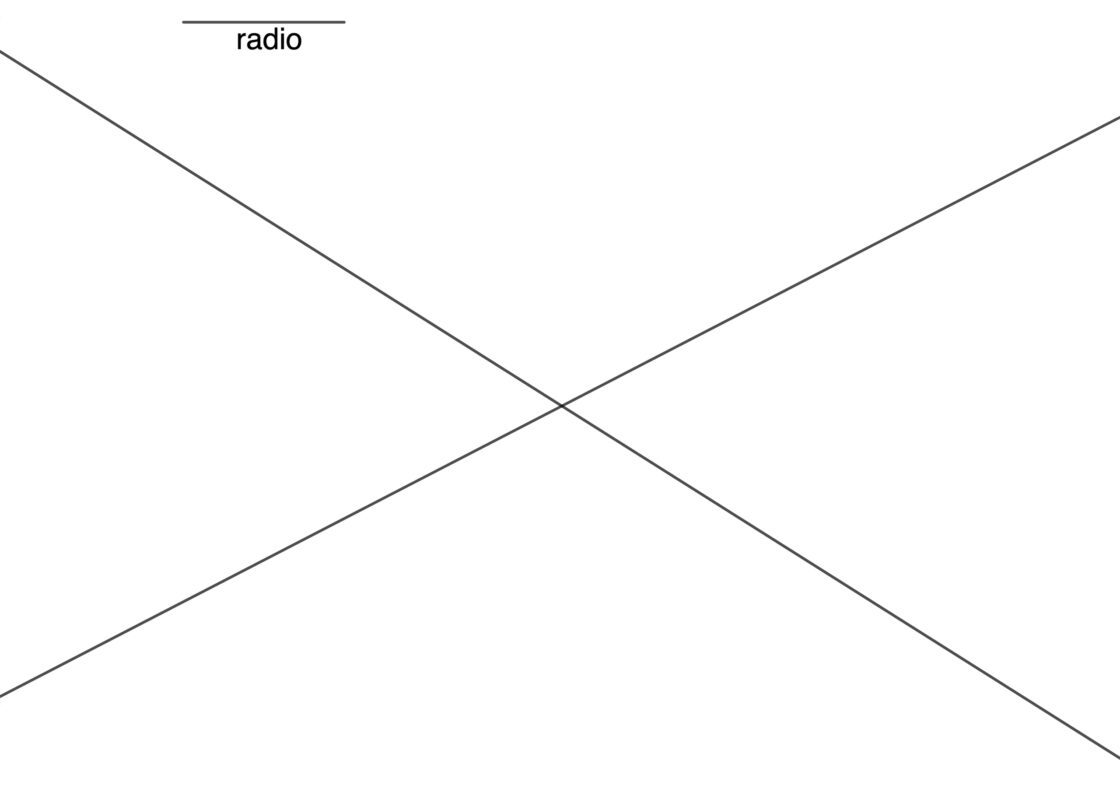
- Dibuja una perpendicular por un punto cualquiera P de la recta t.
- Sobre esa perpendicular, mide el radio r de las soluciones que nos piden. Así obtienes los puntos R y S.
- Traza paralelas a la recta t que pasen por R y S.
- Ahora dibuja una perpendicular a la recta s por cualquier punto Q de la misma.
- Mide el radio r de las soluciones sobre esa perpendicular que acabas de dibujar. De ese modo obtienes V y T.
- A continuación, dibuja paralelas a la recta s que pasen por V y T.
- Los puntos donde todas esas paralelas se cortan, son los centros de las circunferencias que estás buscando.
- Con radio en cada uno de esos puntos, a los que puedes llamar O1, O2, O3 y O4, traza circunferencias con el radio de la solución.
En la siguiente aplicación interactiva puedes ver el resultado. Puedes mover los puntos para ver que el resultado se cumple de forma independiente a la posición de las rectas o el radio de la solución.
Circunferencias tangentes a una circunferencia y una recta
Para éste problema tendrás el radio r de la solución buscada, una recta s cualquiera y una circunferencia de centro O1. Hay tres posibilidades distintas respecto al dibujo de circunferencias tangentes a una circunferencia y una recta. Estos serían:
- La circunferencia y la recta están separados.
- La circunferencia y la recta son tangentes.
- La circunferencia y la recta se cortan, es decir, son secantes.
El procedimiento es exactamente el mismo en los tres casos. La apariencia final puede cambiar, pero los pasos a seguir van a ser los mismos en los tres tipos de problemas. Para este ejemplo, vas a dibujar el caso en el que son secantes. Tu punto de partida pues, será semejante a lo siguiente:
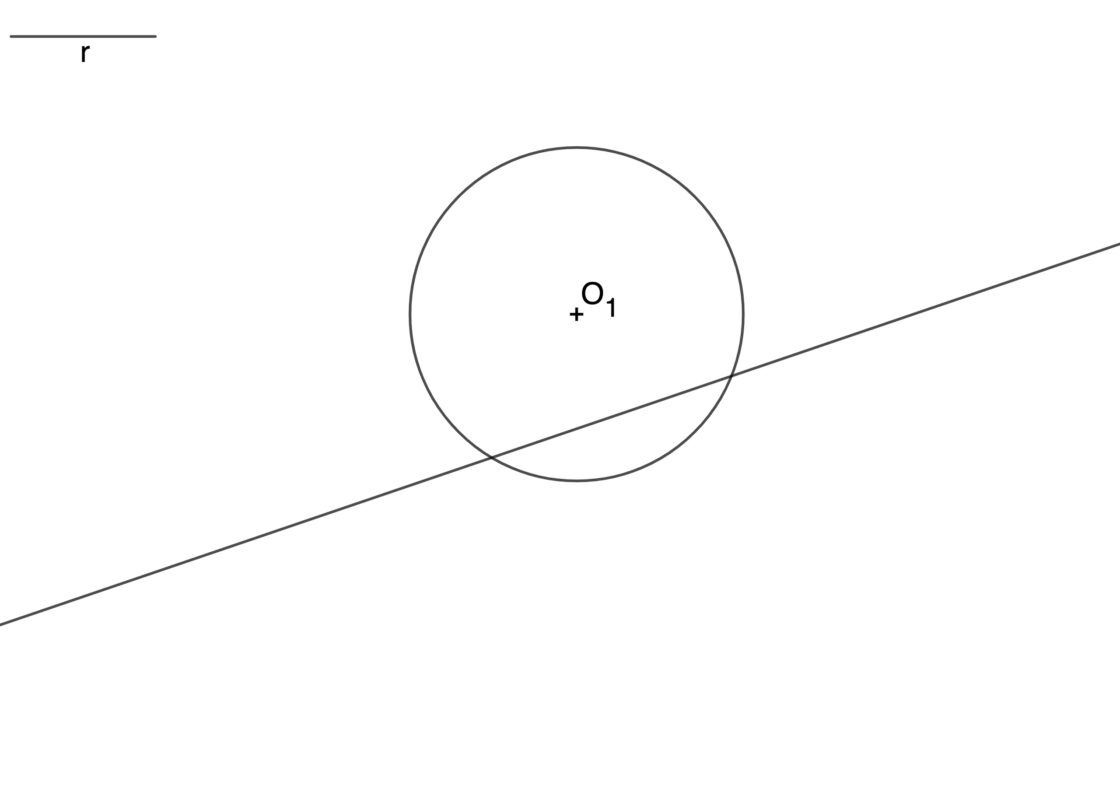
- Empieza por marcar un punto cualquiera sobre la recta s al que puedes llamar P.
- Dibuja una perpendicular a la recta s que pasa por P.
- Sobre esa perpendicular que acabas de dibujar, mide el radio r de la solución. De ese modo obtienes los puntos R y S.
- Traza paralelas a la recta s que pasen por R y S.
- Ahora realiza una recta t con centro en O1 y que corte a la circunferencia inicial en cualquier punto T.
- A continuación de T, mide el radio r de las circunferencias solución. El punto resultante lo puedes llamar V.
- Con centro en O1 y radio hasta V, dibuja una circunferencia.
- Los puntos donde se cortan esa circunferencia que acabas de trazar y las paralelas que dibujaste antes, son los centros O2, O3, O4 y O5 de las circunferencias que te piden.
Ten en cuenta que si la circunferencia y la recta son tangentes o están separadas, tendrás dos circunferencias. Por otra parte, cuando son secantes, tendrás cuatro.
En la siguiente aplicación interactiva puedes mover los puntos azules para verificar el resultado y cada uno de los casos por separado.
Circunferencias tangentes a dos circunferencias
Cuando hablamos de circunferencias tangentes a otras dos circunferencias varias situaciones posibles:
- Que las circunferencias estén separadas. A su vez tienes otras cuatro posibilidades:
- Que el radio de la solución sea menor que el radio de cualquiera de las dos circunferencias sumado a la distancia entre ambas. Tendrás dos soluciones posibles.
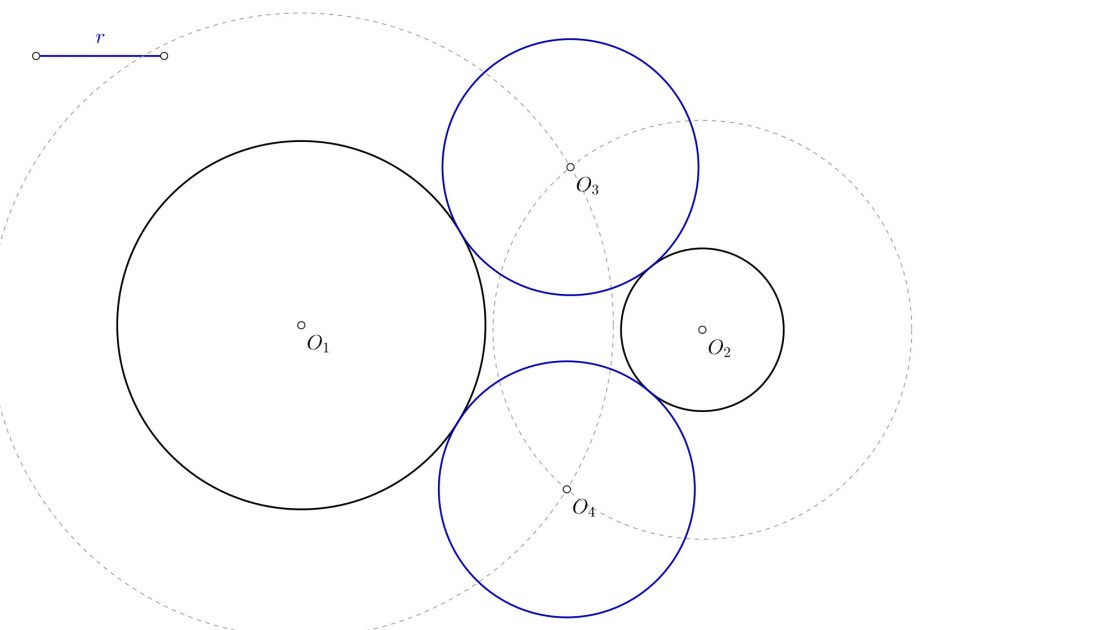
- Que el radio de la solución sea mayor que el radio de una de las dos circunferencias sumado a la distancia que las separa. Tendras cuatro circunferencias. Dos de ellas estarán fuera, y otras dos tendrán dentro una de las dos circunferencias.
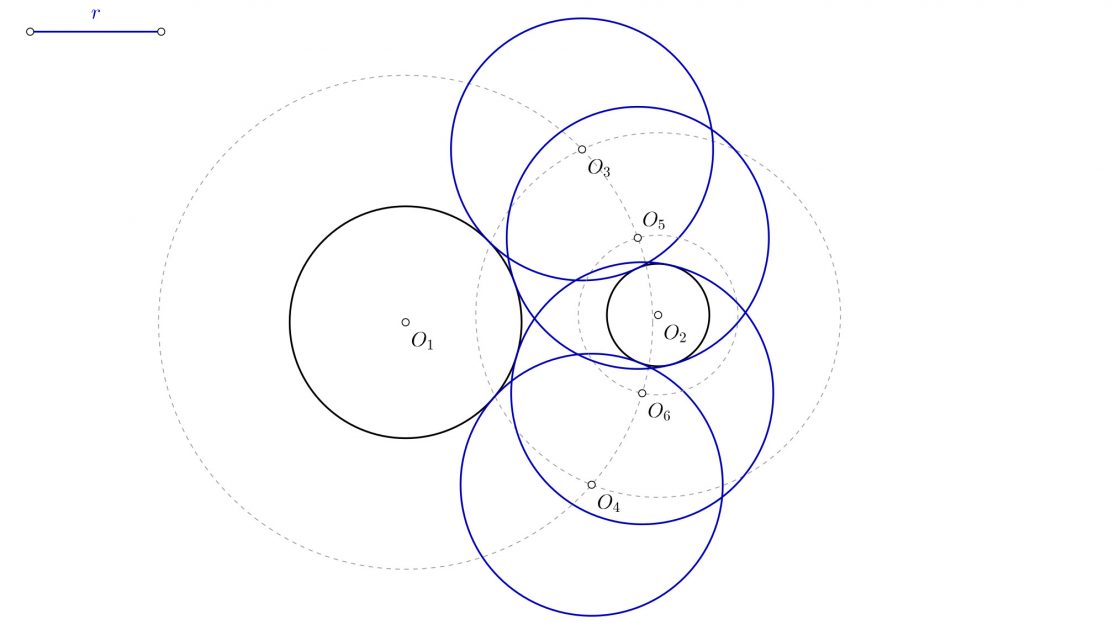
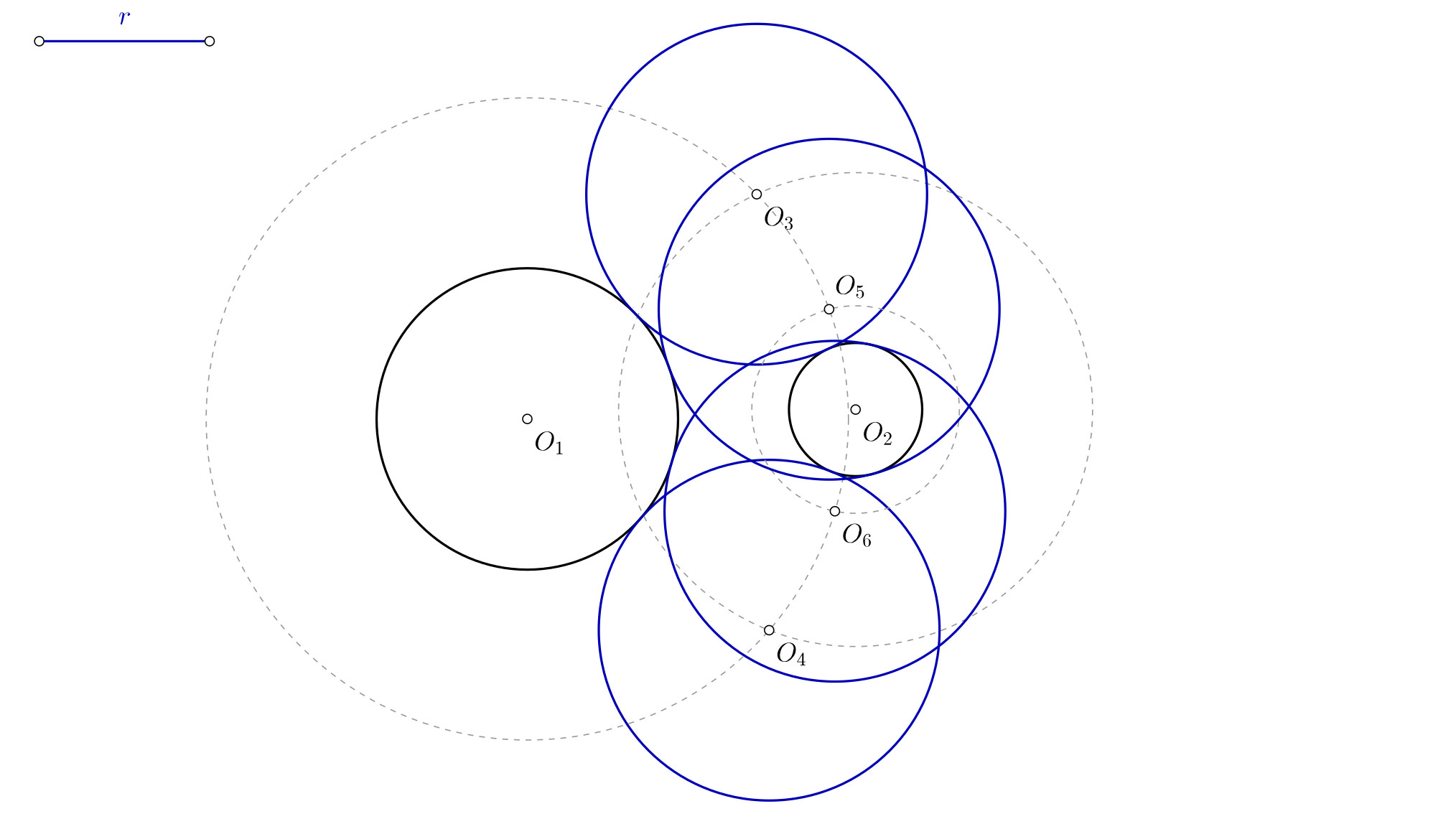
- Que el radio de la solución sea mayor que la suma de cualquiera de las dos circunferencias y la distancia que las separa, pero menor que la suma de ambas circunferencias y la distancia entre ellas. Tendrás seis circunferencias posibles. Dos exteriores a ambas, y otras dos contendrán una de ellas y tendrán fuera a la otra.
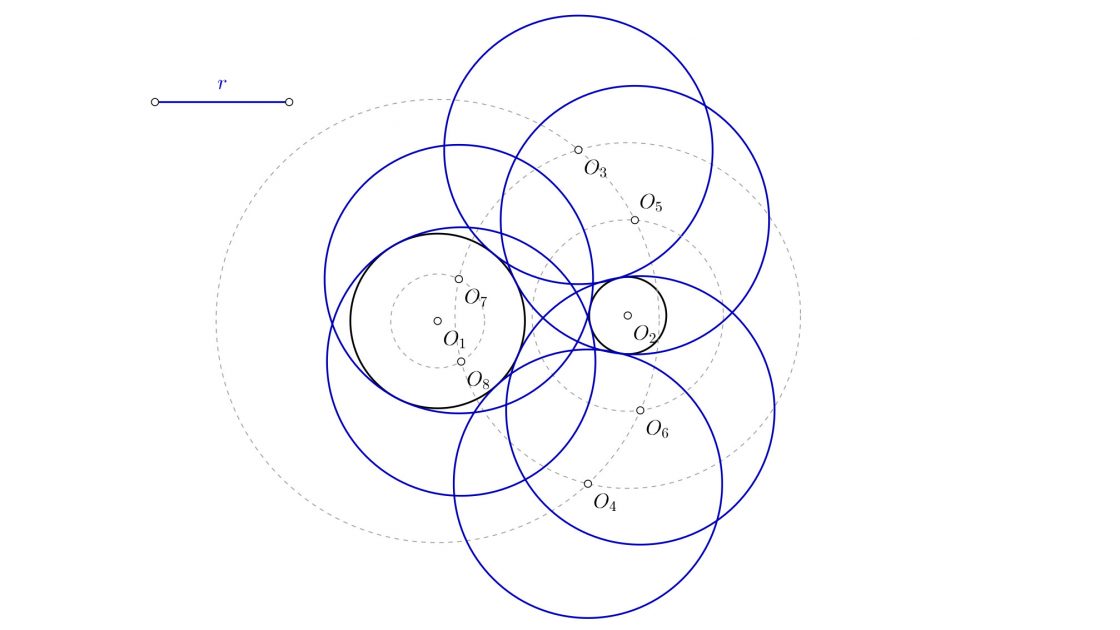
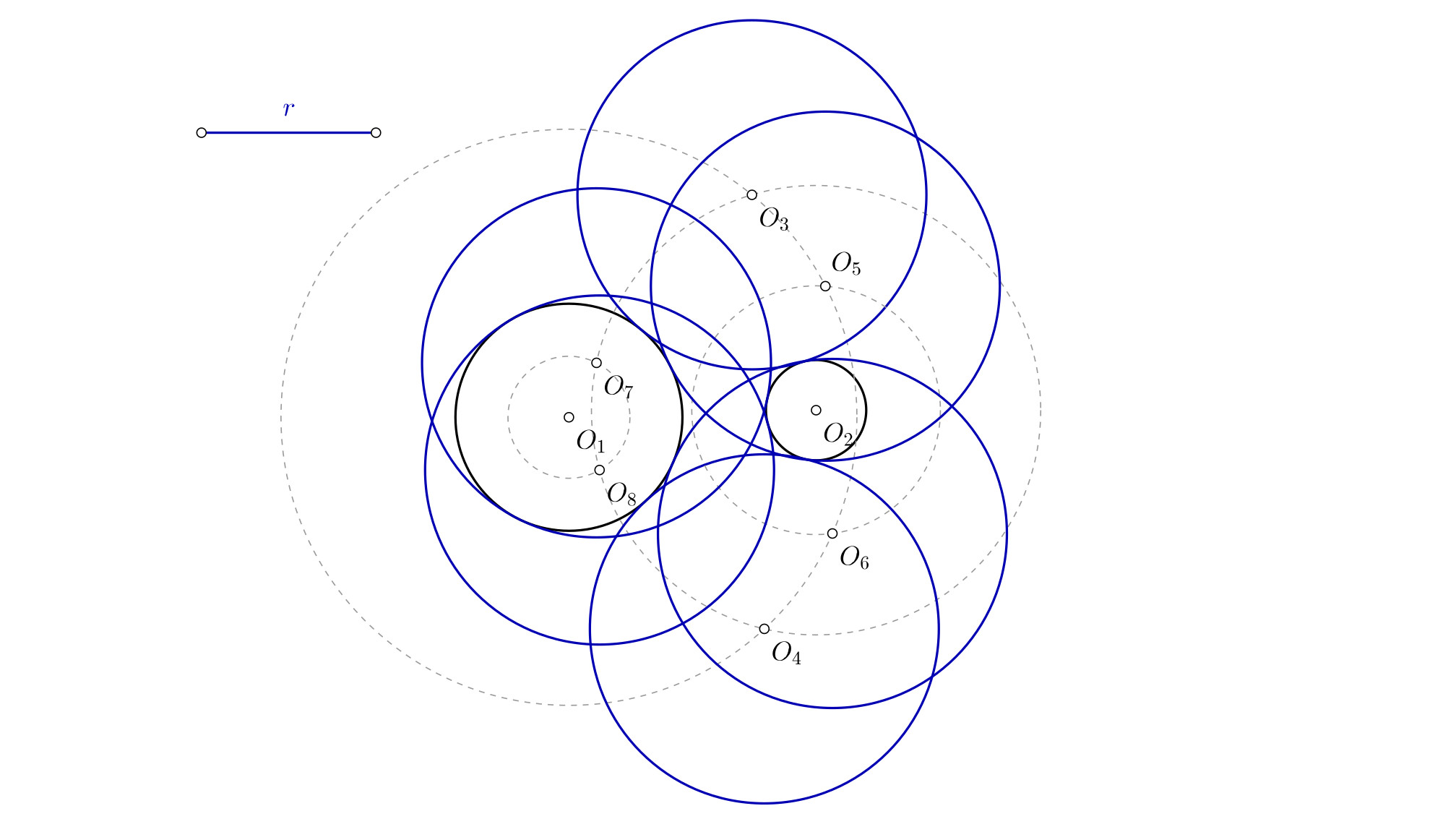
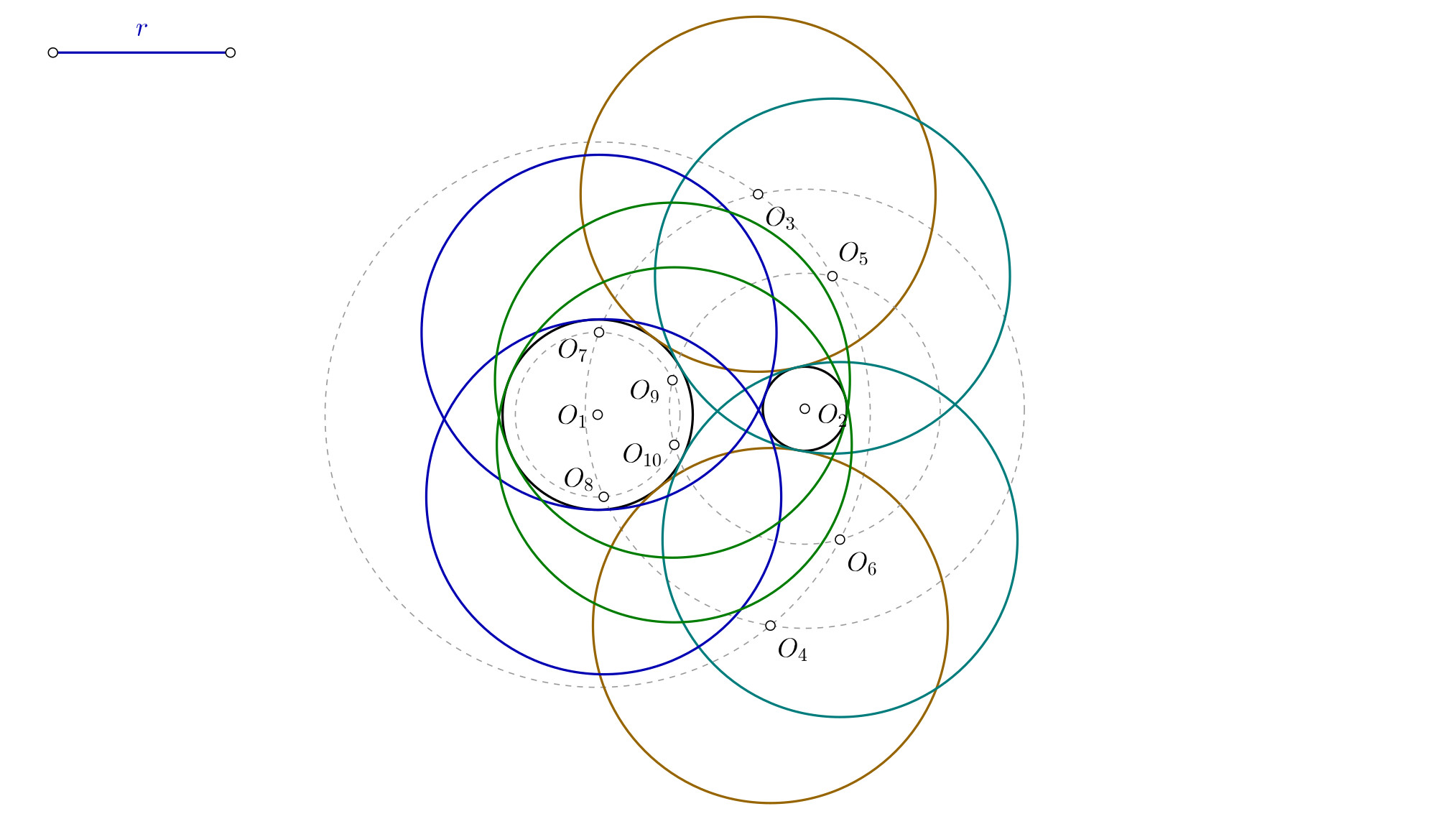
- Que el radio de la solución sea mayor que la suma de ambas circunferencias y la distancia que las separa. Tendrás ocho posibles soluciones: Dos fuera de ambas circunferencias, dos contendrán a ambas circunferencias. Las otras cuatro tendrán una dentro, y la otra fuera.
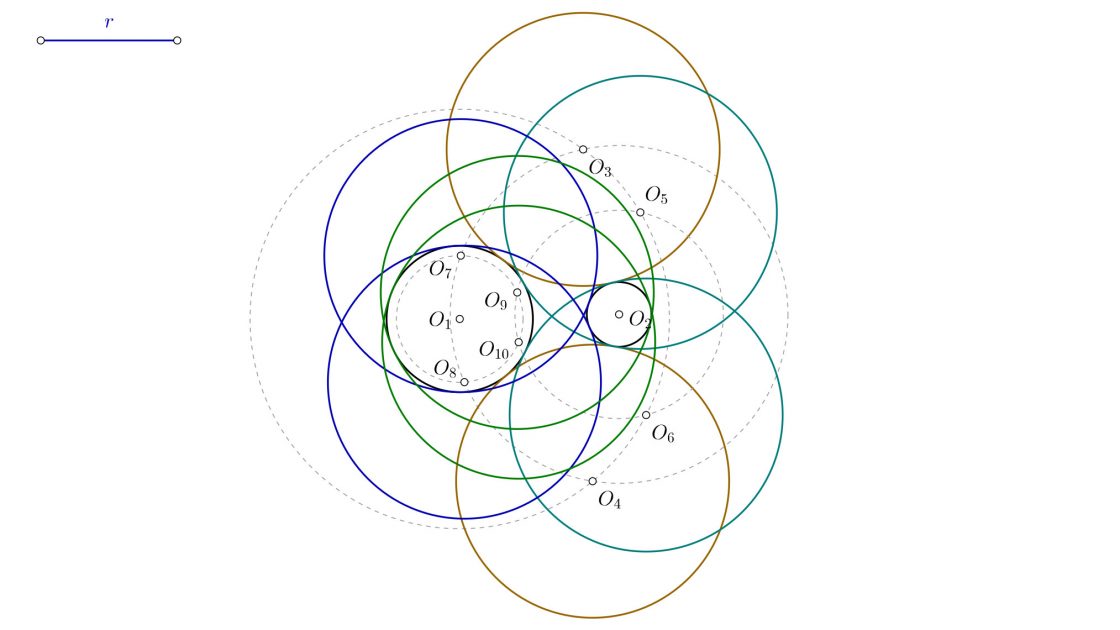
- Que el radio de la solución sea menor que el radio de cualquiera de las dos circunferencias sumado a la distancia entre ambas. Tendrás dos soluciones posibles.
- También puede pasar que las circunferencias sean tangentes. En cuyo caso tendrás también cuatro posibles soluciones.
- Que el radio de la solución sea menor que la suma de ambas circunferencias y que cualquiera de las circunferencias. En éste caso tendrás cuatro circunferencias, dos interiores y dos exteriores.
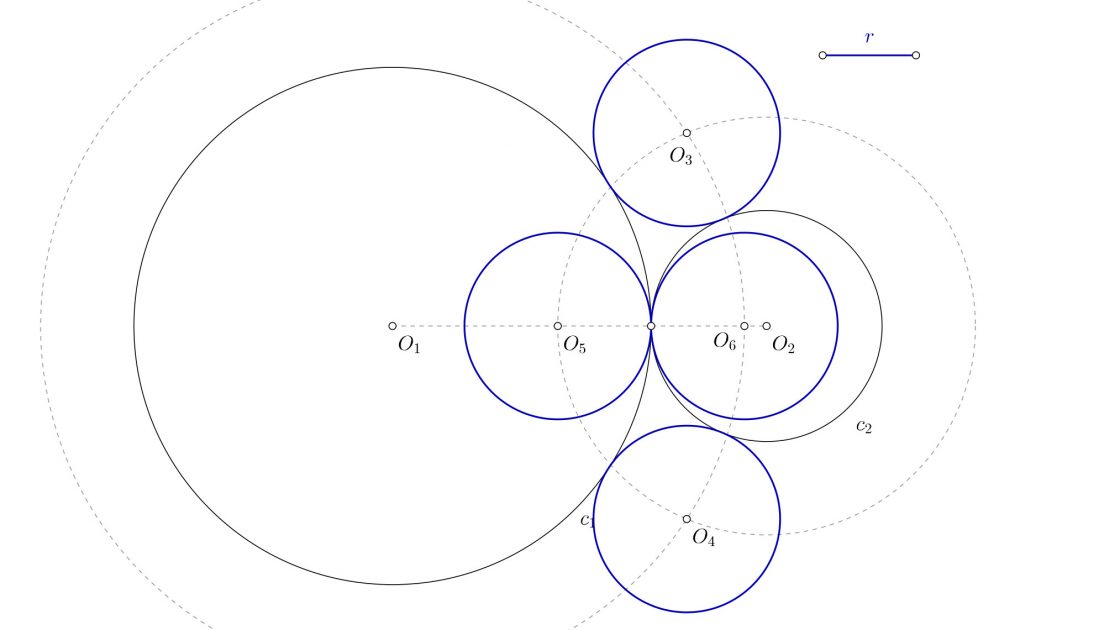
- Que el radio de la solución sea mayor que una de las dos circunferencias y menor que la otra. Tendrás una circunferencia interior y tres exteriores, una de las cuales contendrá a una de las circunferencias inciales.
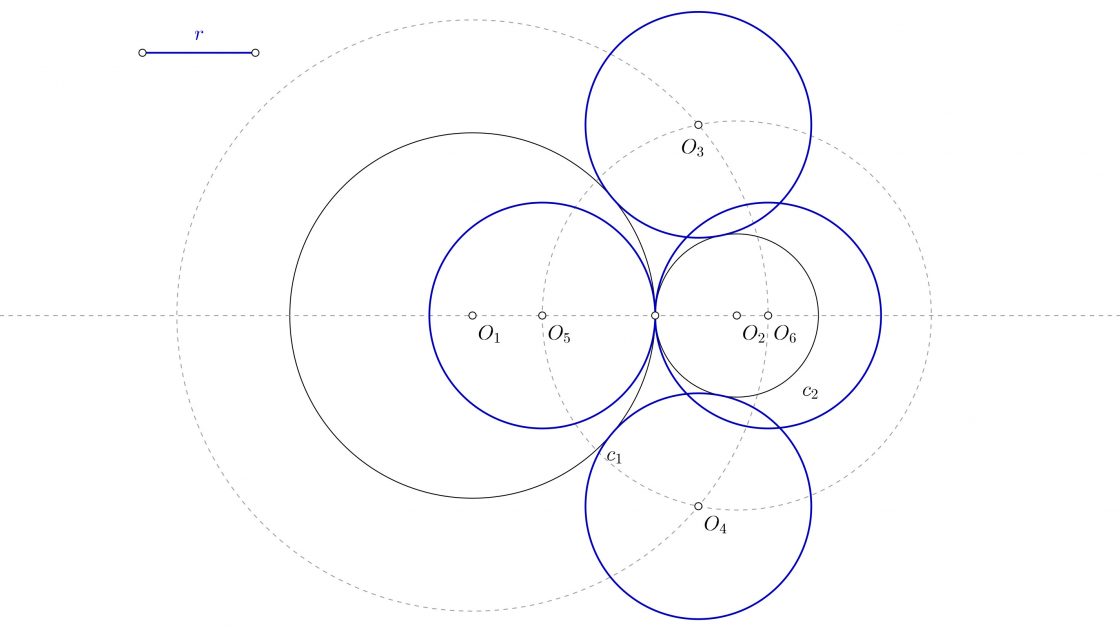
- Que el radio de la solución sea mayor que cualquiera de las dos circunferencias, pero menor que la suma de ambas. Tendrás cuatro circunferencias exteriores, dos de las cuales contendrán a las circunferencias iniciales.
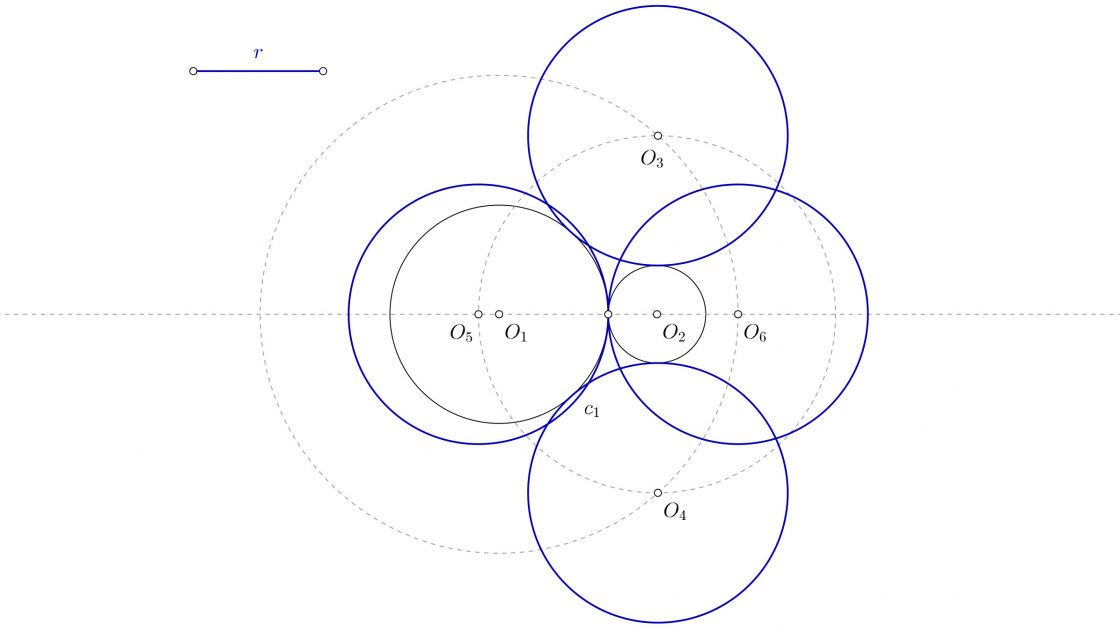
- Que el radio de la solución sea mayor que la suma de las circunferencias iniciales. Tendrás seis circunferencias, dos exteriores, dos que contendrán a cada una de las circunferencias iniciales, y otro par más que contendrán a las dos circunferencias iniciales.
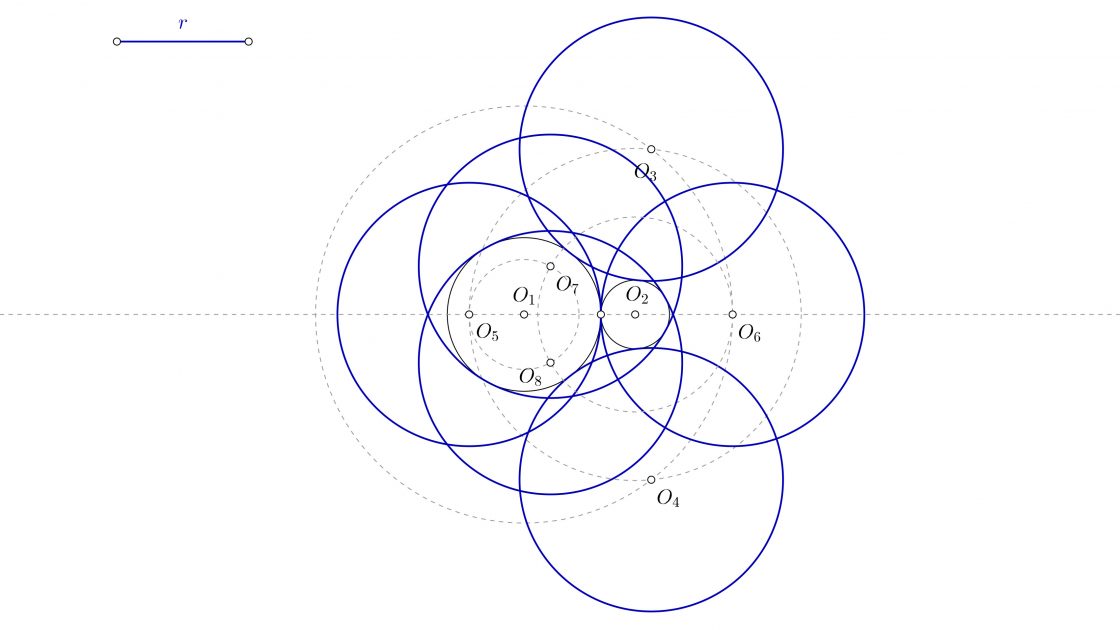
- Que el radio de la solución sea menor que la suma de ambas circunferencias y que cualquiera de las circunferencias. En éste caso tendrás cuatro circunferencias, dos interiores y dos exteriores.
- También puede pasar que las circunferencias sean secantes. Al igual que en los casos anteriores, se presentan varias opciones:
- Que el radio de la solución sea sea tan grande que no permita dibujar circunferencias interiores, pero no tan grande como para contener a las dos circunferencias iniciales. Habrá solo dos circunferencias resultantes.
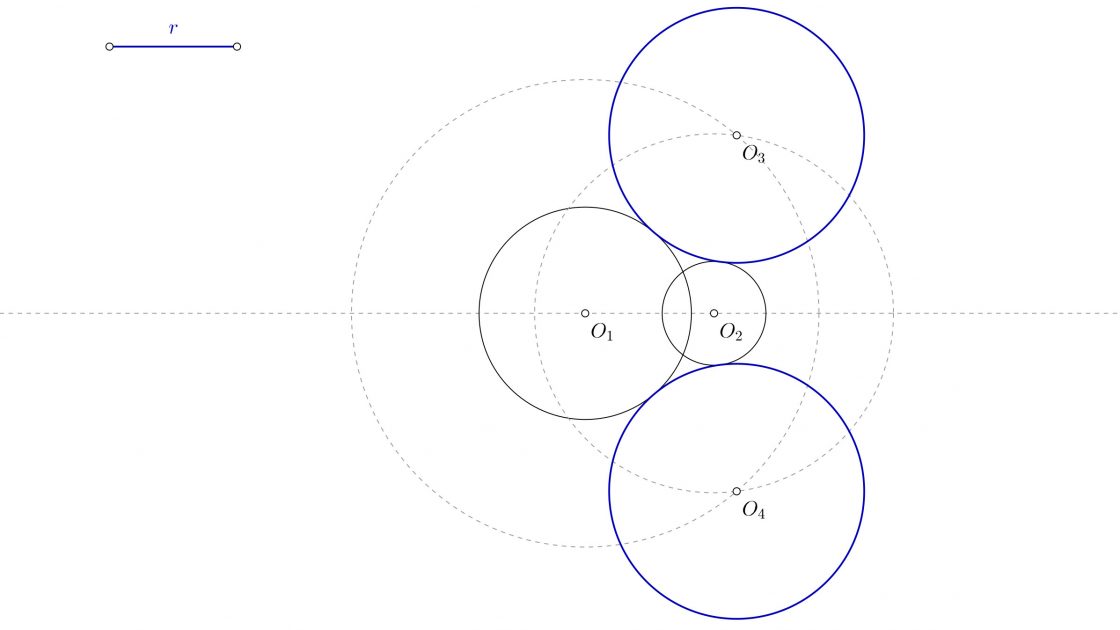
- Que el radio de la solución sea tan grande que pueda incluir ambas circunferencias, en cuyo caso habrá cuatro circunferencias. Dos exteriores y dos que contendrán a las circunferencias iniciales.
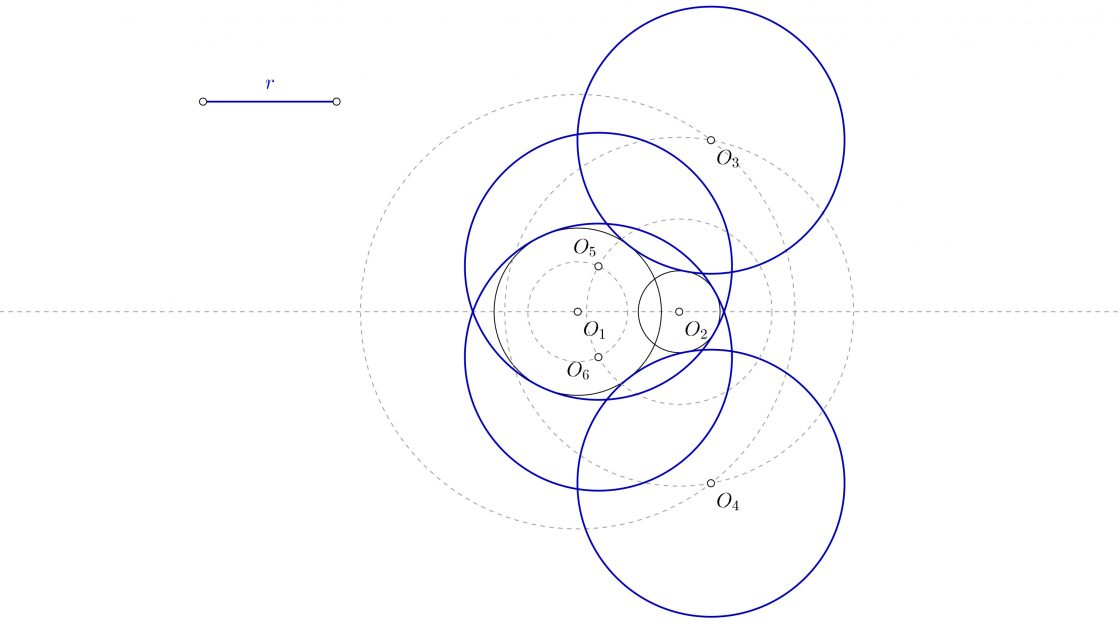
- Que el radio sea tan pequeño que permita dibujar dos circunferencias exteriores, dos interiores dentro de cada circunferencia inicial, y otras dos dentro de la intersección de las dos circunferencias iniciales. En total habrá ocho posibles circunferencias.
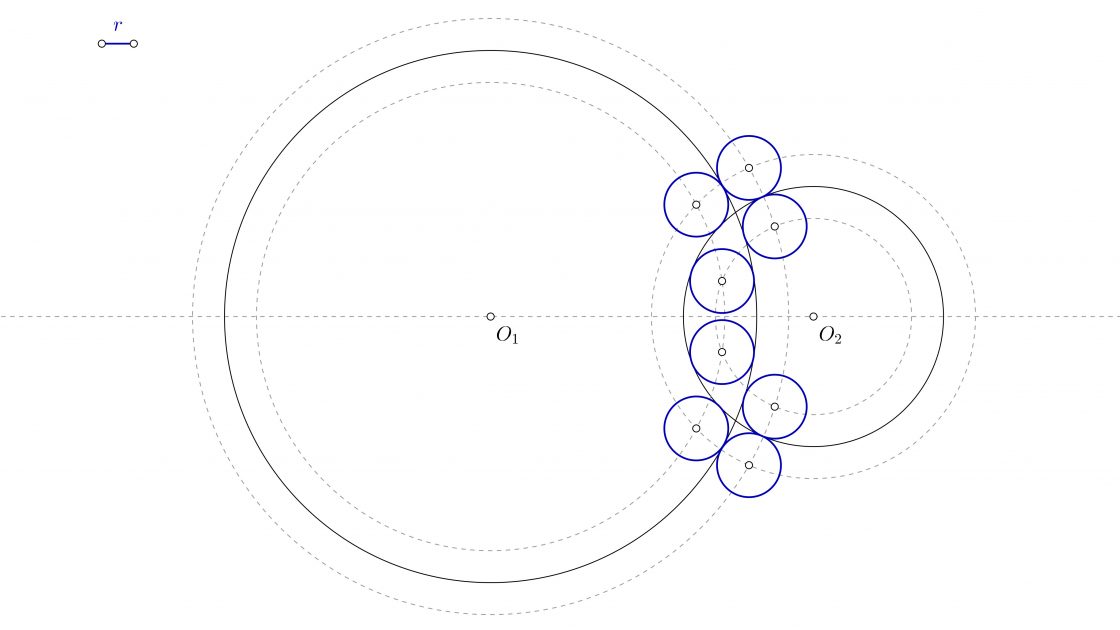
- Parecido al caso anterior, pero el espacio disponible en la intersección de ambas circunferencias solo permite dibujar seis posibles circunferencias.
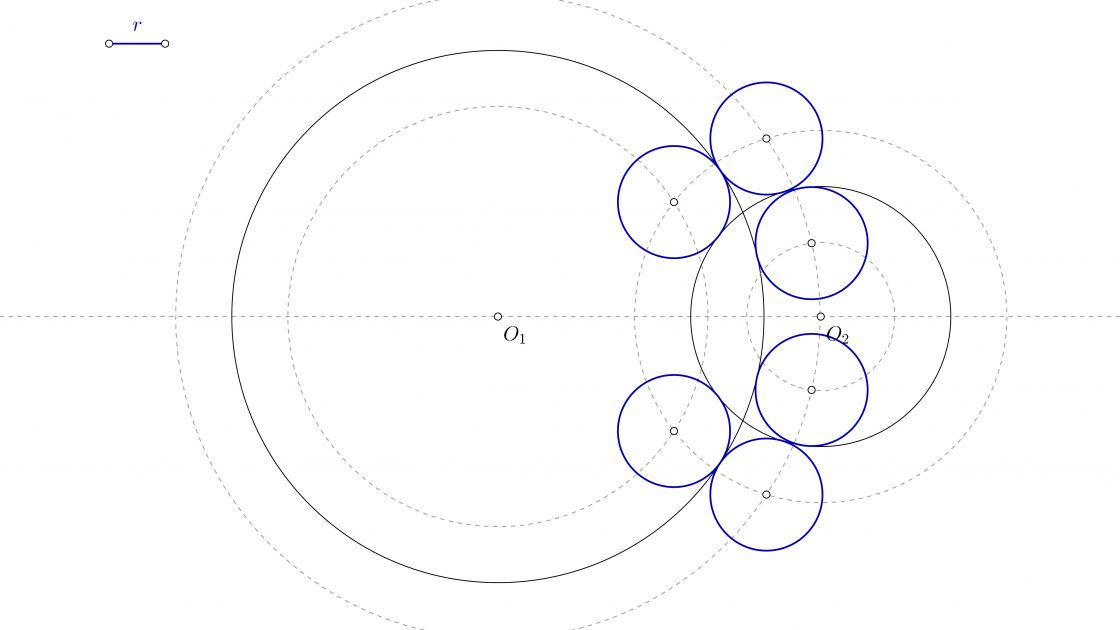
- Puede pasar que el radio permita dibujar dos circunferencias interiores a una de las circunferencias iniciales, y dos exteriores.
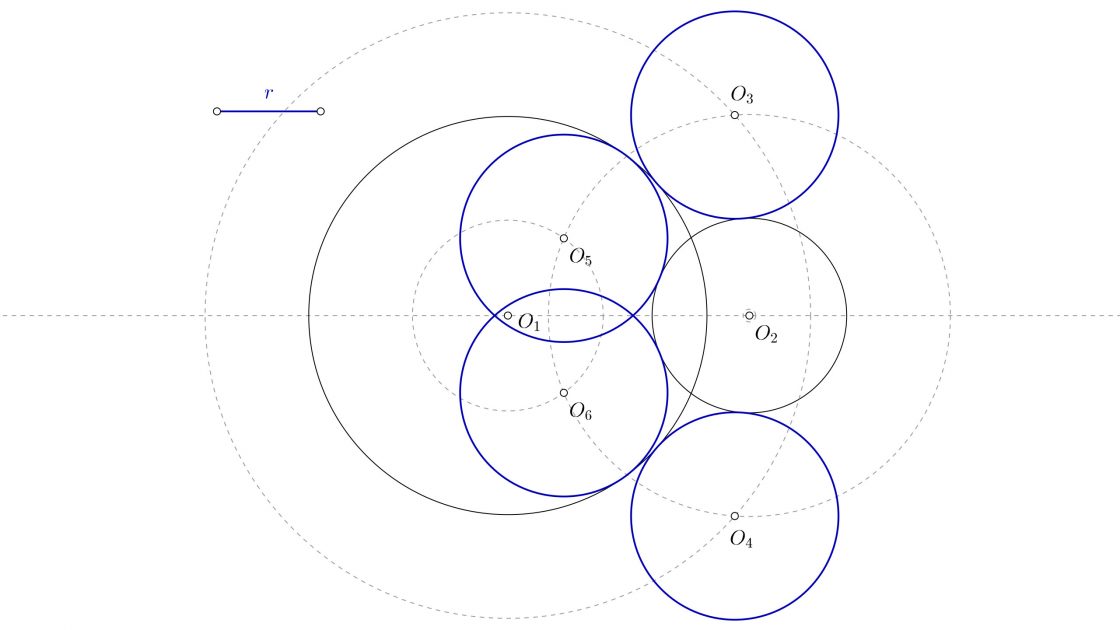
- Que el radio de la solución sea sea tan grande que no permita dibujar circunferencias interiores, pero no tan grande como para contener a las dos circunferencias iniciales. Habrá solo dos circunferencias resultantes.
¿Cómo resolver éste problema?
Te voy a explicar por separado un par de posibilidades distintas, para no complicar demasiado la explicación. Luego si te encuentras en la situación de que te pregunten por todas las circunferencias posibles, solo tienes que combinar las distintas explicaciones en el mismo ejercicio. Voy a emplear las circunferencias que están separadas porque son las más habituales. De todas formas, el proceso es exactamente el mismo cuando son tangentes o si son secantes.
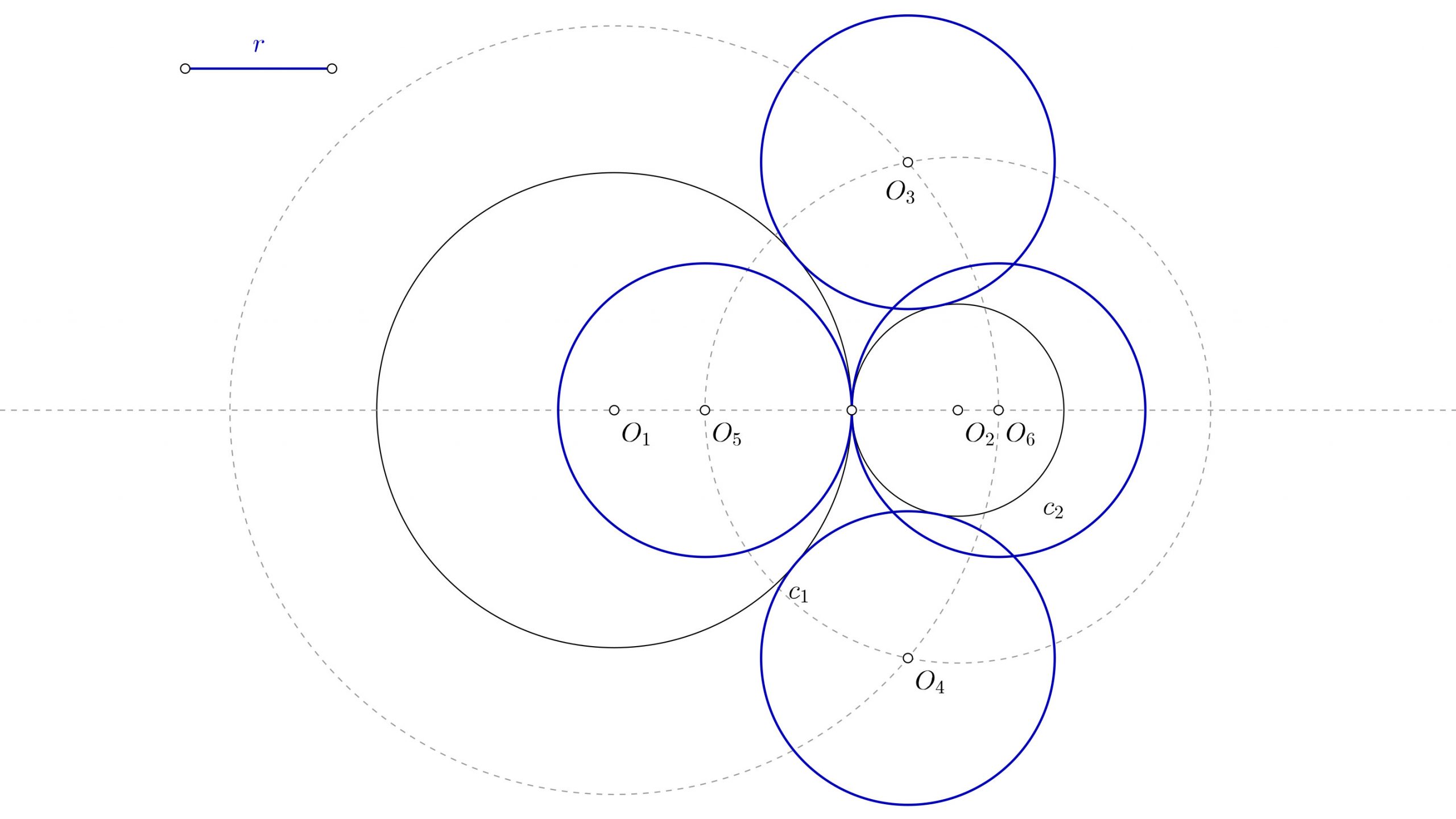
Circunferencias tangentes exteriores a dos circunferencias
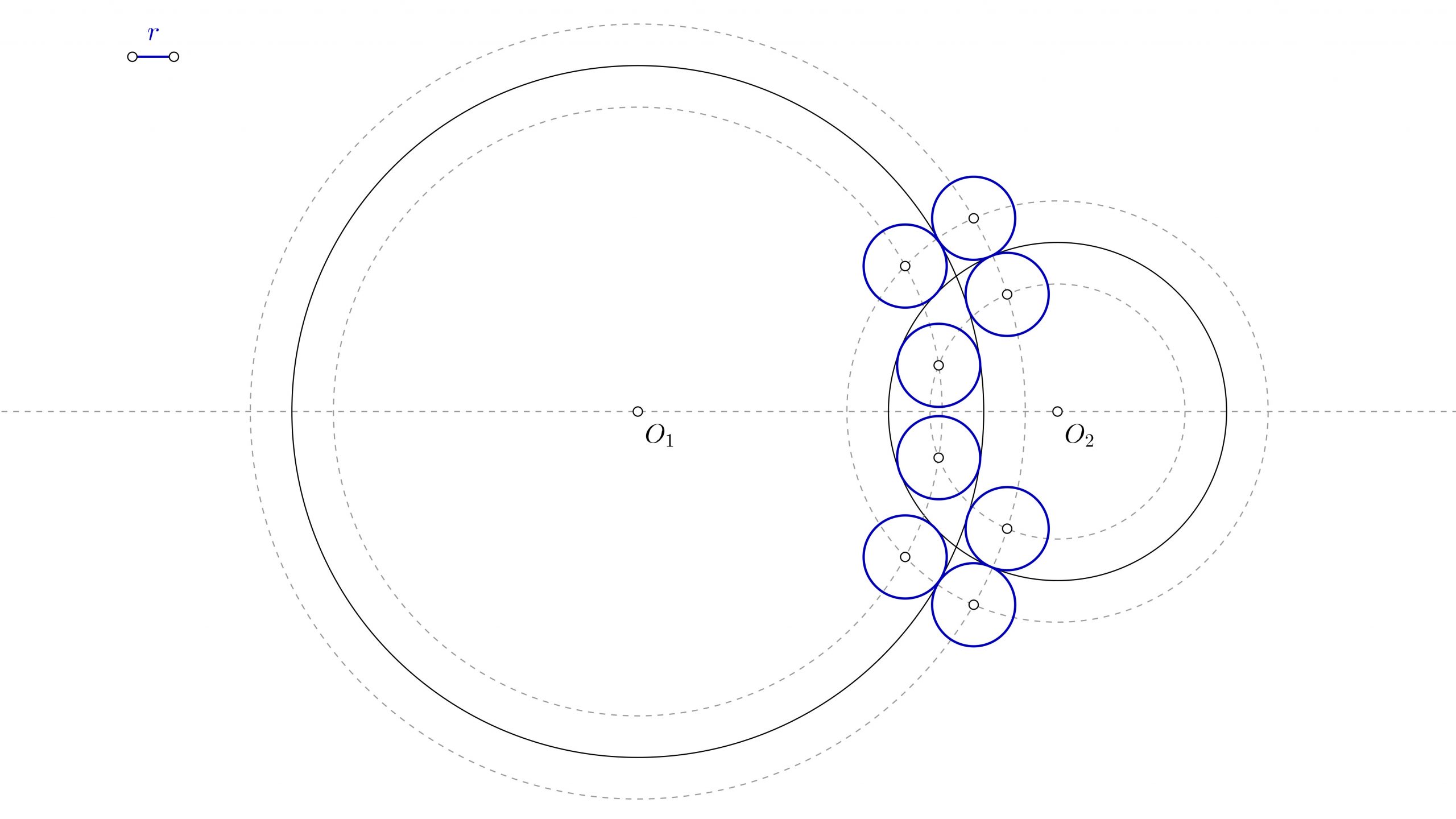
Los datos iniciales son dos circunferencias de centros O1 y O2, y el radio r de las soluciones que te piden. Tu punto de partida será similar a esto:
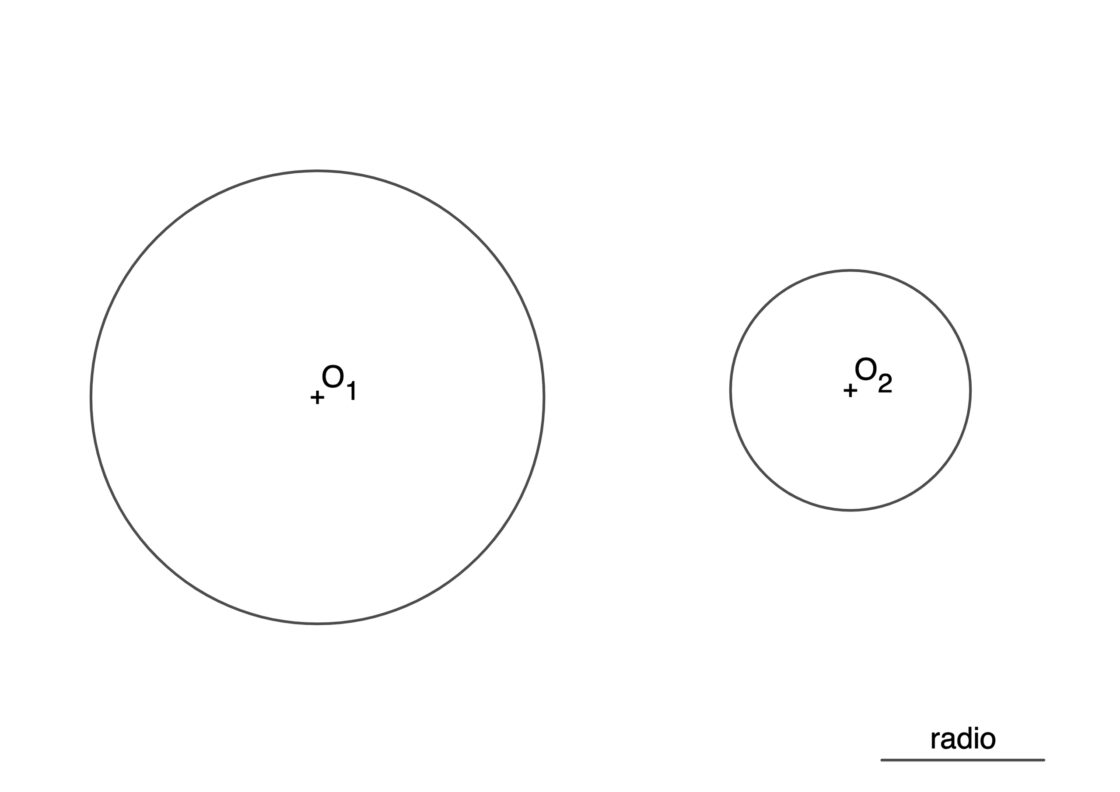
- Para empezar, marca un punto cualquiera P sobre la circunferencia de centro O1.
- Dibuja la recta que parte de O1 y pasa por P.
- Sobre esa recta que acabas de dibujar, y con centro en P, marca el tamaño del radio r. Ese será el punto R.
- Ahora dibuja con centro en O1 y radio hasta R una circunferencia.
- Marca un punto Q en la otra circunferencia.
- Dibuja la recta que pasa por O2 y Q.
- A partir de Q, marca lo que mide el radio r. Así tendrás el punto S.
- Con centro en O2 y radio hasta S, dibuja una circunferencia.
- Los puntos donde las circunferencias que pasan por R y S se cortan, serán los centros O3, O4 de las soluciones buscadas.
Si quieres hallar los puntos de tangencia, solo tienes que unir los centros de las circunferencias y ver donde cortan.
Ten en cuenta que si las circunferencias están separadas y el radio de la solución es tan pequeño que no puede abarcar a ninguna de las dos iniciales, se resuelve exactamente igual. Ese es uno de los problemas de tangencias más típicos que te puedes encontrar.
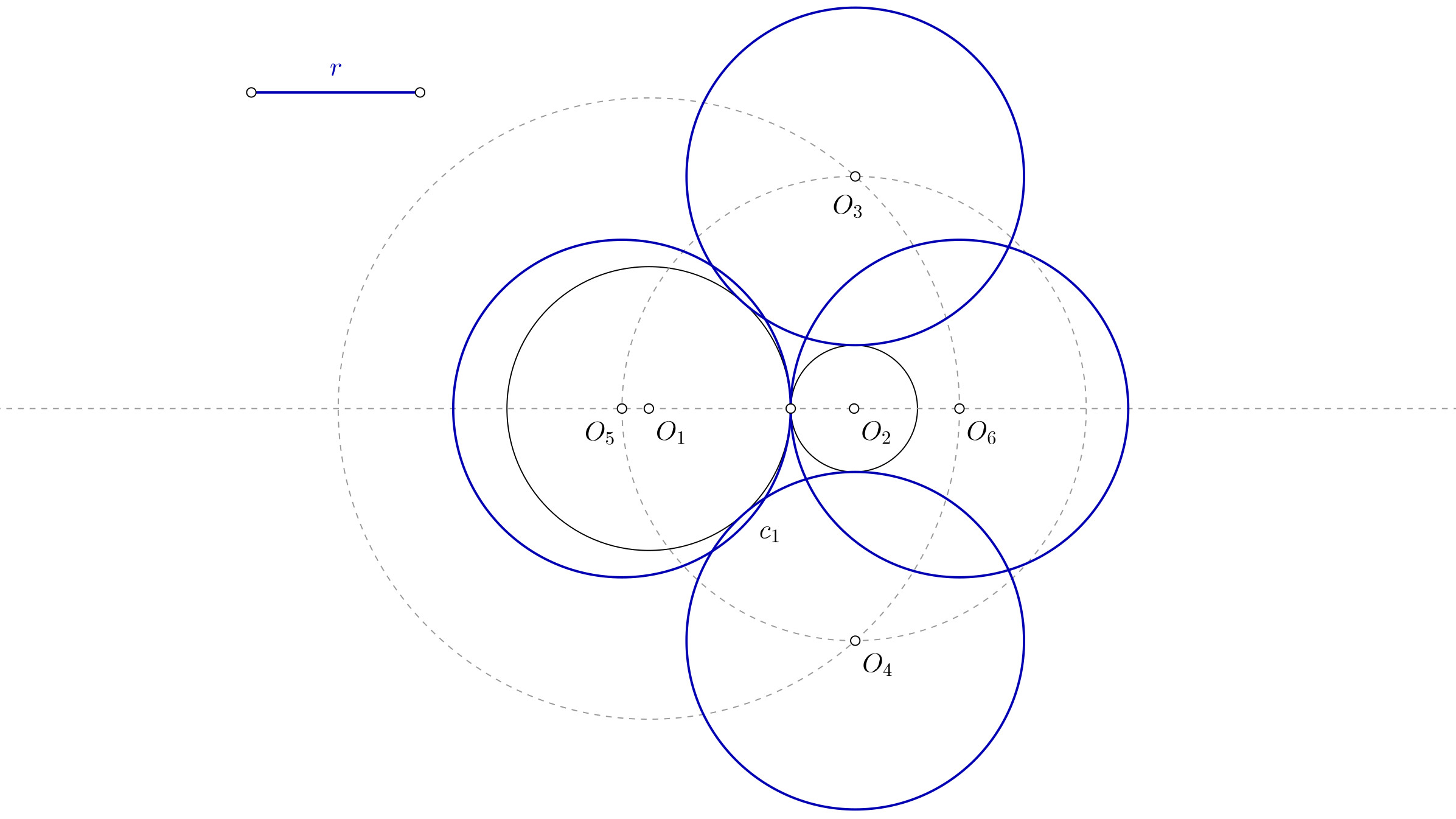
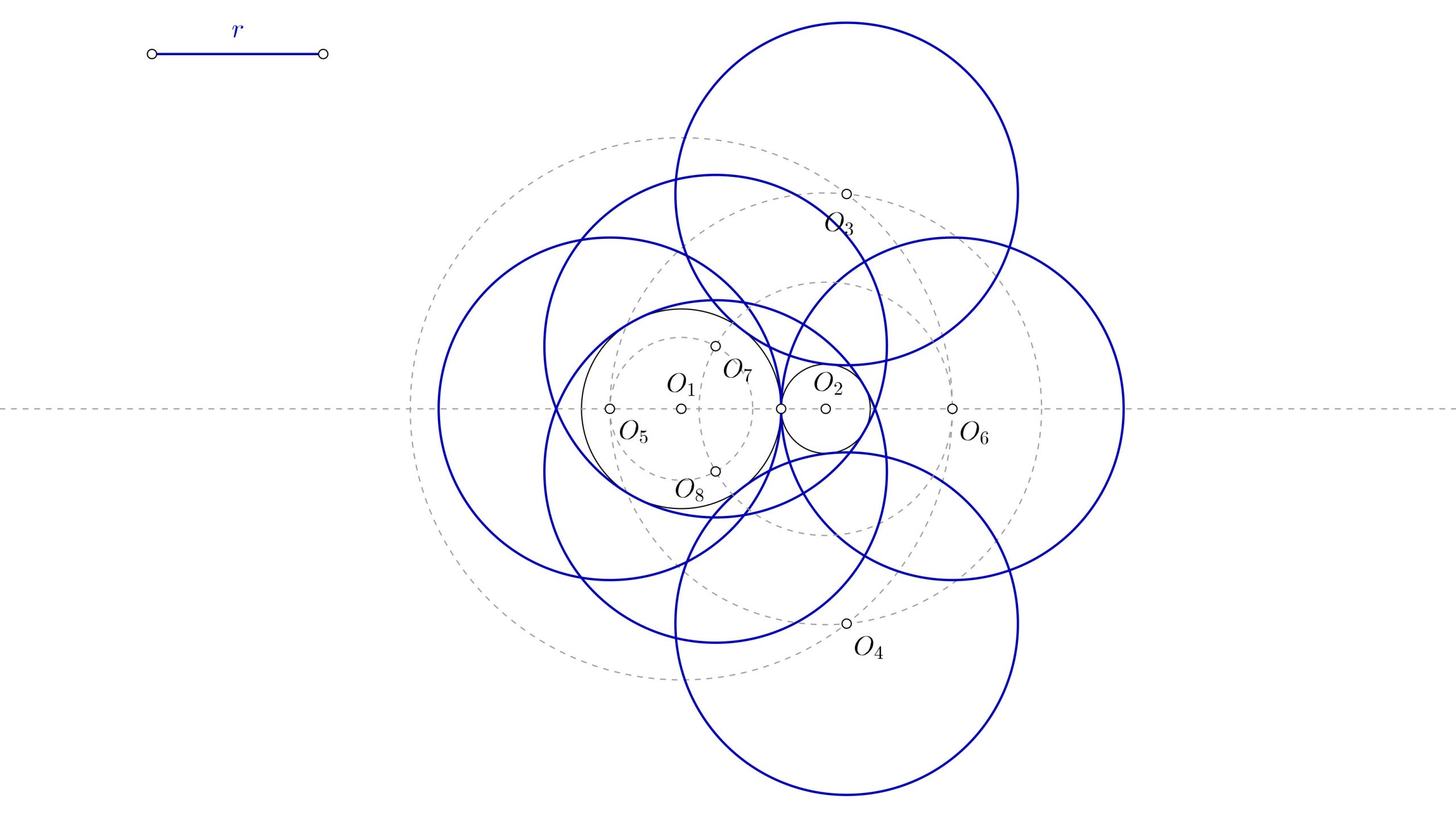
Tangentes que contienen a las circunferencias
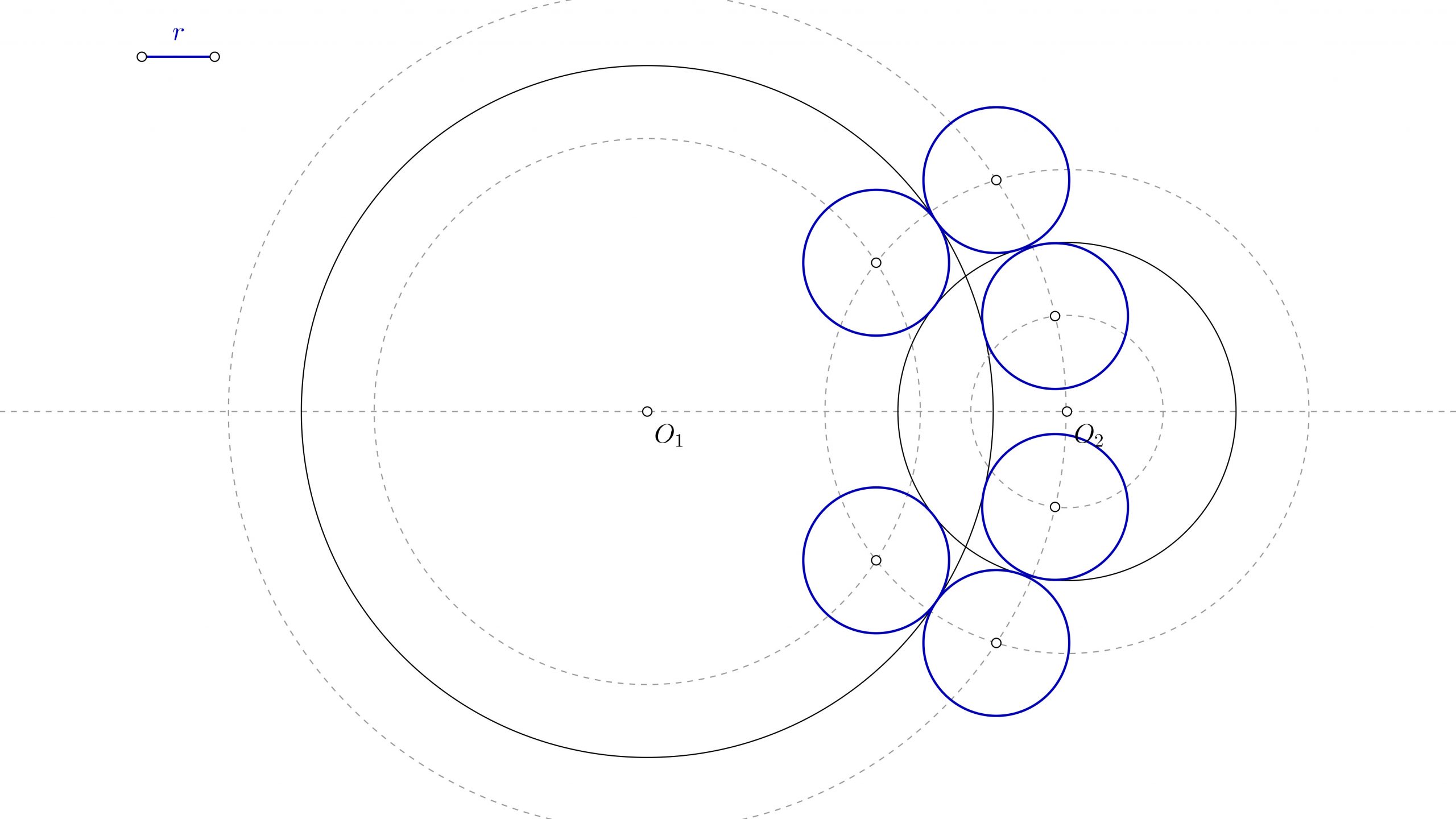
Esto puede ocurrir si el radio de la solución es más grande que la mayor de las circunferencias, y mayor que la mitad de la distancia entre los dos puntos más alejados de las circunferencias.
- Empieza por marcar un punto cualquiera sobre la circunferencia de centro O1. A ese punto llámalo P.
- Prolonga la línea que une O1 con P y con centro en O1, marca el radio de la solución. Así tienes el punto R.
- Ahora con centro en R, y en dirección a O1, marca el radio de esa circunferencia. Verás en la imagen que lo he llamado s para que puedas identificarlo. Así obtienes el punto X.
- Dibuja una circunferencia con centro O1 y radio hasta X.
- Marca un punto cualquiera sobre la circunferencia de centro O2, puedes llamarlo Q.
- Prolonga la recta que une O2 con Q, y con centro en O2, mide el radio de la solución. El punto que obtienes es S.
- Desde S, y en dirección a O2, mide el radio de esa circunferencia. En la imagen verás que yo lo he llamado t para poder identificarlo. De esa manera marcas el punto Y.
- Con centro en O2 y radio hasta Y, realiza una circunferencia. Los puntos donde esta circunferencia corta a la de centro O1 y radio hasta X te están indicando los centros de las circunferencias que buscas, que serán O3 y O4.
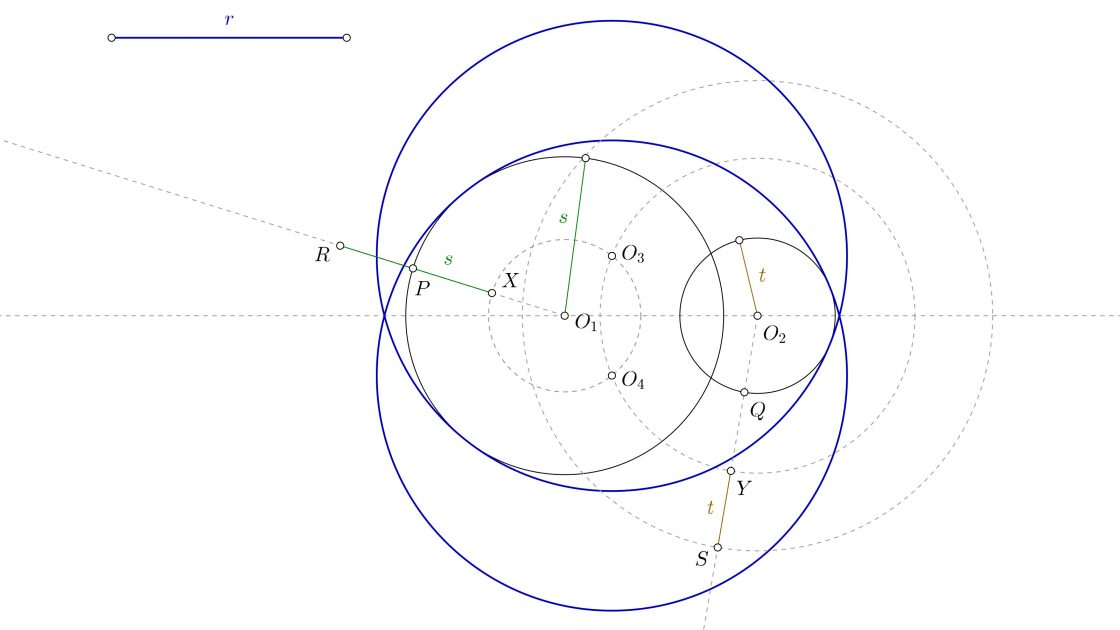
Experimenta en la siguiente aplicación interactiva moviendo los puntos y los objetos para verificar el resultado y ver todas las combinaciones posibles. Te recomiendo ponerlo a pantalla completa para verlo mejor.