Circunferencia tangente a tres circunferencias tangentes

Este es un caso particular del problema de Apolonio, y se puede resolver de la misma manera que se resuelve éste. Por si no lo recuerdas, el problema de Apolonio es el que explica como hallar las circunferencias tangentes a tres circunferencias dadas. Ese tipo de problemas de tangencias se suelen plantear en el nivel de segundo de bachillerato. Pero también está relacionado con un problema más sencillo que se suele explicar en primero de bachillerato, que explica como hallar tres circunferencias tangentes entre si cuando lo único que conoces son sus centros. A continuación te explicaré un procedimiento muy sencillo para hallar la circunferencia tangente a tres circunferencias que son tangentes entre si.

Circunferencia tangente a tres circunferencias tangentes entre si

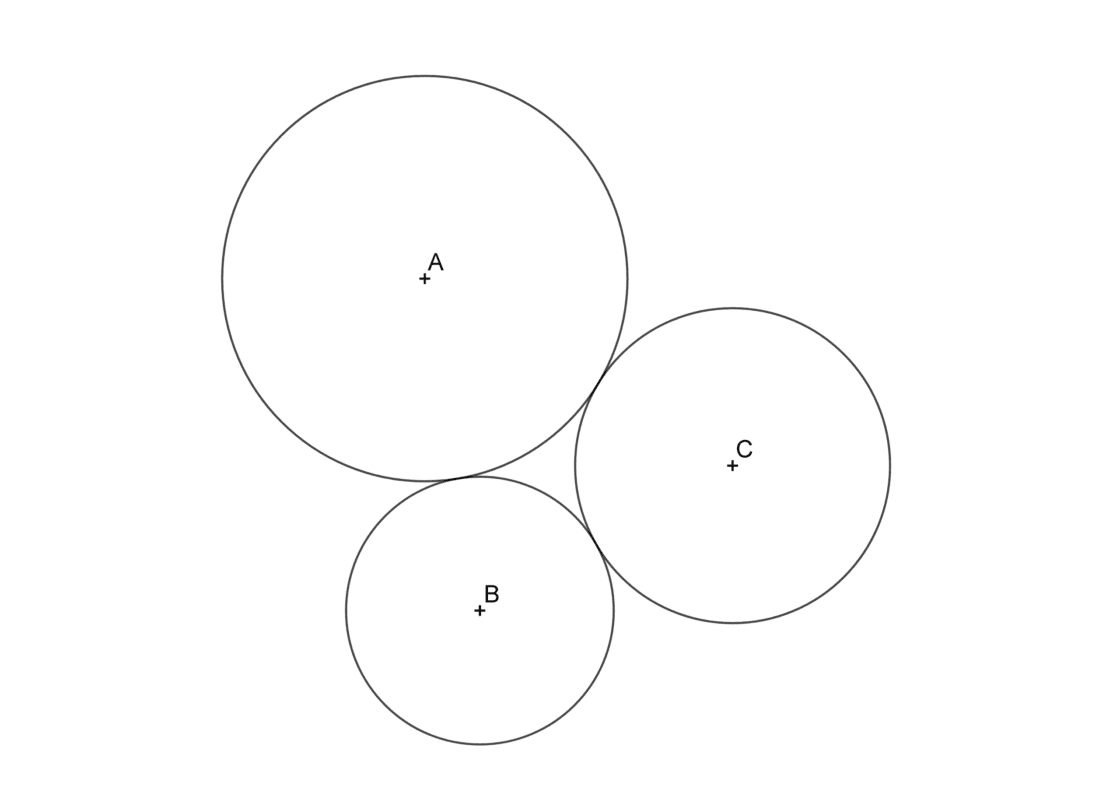
Como indica el ejercicio, tu punto de partida son tres circunferencias tangentes entre si, por lo tanto será algo parecido a esto:

Aquí abajo tienes un vídeo con todo el proceso explicado paso a paso, y un poco más abajo, la transcripción.

La solución de este ejercicio está basada en los conceptos de potencia e inversión. Pero para no hacer demasiado farragosa esta explicación, iré al grano y te explicaré como resolverlo de manera sencilla.

• Empieza por seleccionar los centros de dos circunferencias cualquiera. En este caso yo he elegido A y B. Dibuja la recta que pasa por ellos y marca el punto de tangencia de esas dos circunferencias. Yo lo he llamado T.
• Dibuja una recta perpendicular a esa recta que pasa por el otro centro (en mi caso C).
• Ahora tienes que trazar una circunferencia igual a la de centro C, y que sea tangente a la misma. Dibuja el centro en dirección al segmento AB, no alejándote de él (mira más abajo). Es importante que el centro esté sobre la perpendicular que dibujaste antes. El centro de esa circunferencia es O₁. El punto de tangencia de la circunferencia de centro C y la de centro O₁ es el punto D. Márcalo porque luego lo vas a necesitar.
• Continúa dibujando una recta que pase por O₁ y que sea paralela a la recta que pasa por A y B (también es perpendicular a la línea que pasa por O₁ y C). Esa recta corta a la circunferencia de centro O₁ en los puntos E y F.
• Dibuja líneas que empiecen en T y pasen por D, E y F. Esas rectas cortan a las tres circunferencias en los puntos T₁, T₂ y T₃, que son los puntos de tangencia de la circunferencia exterior tangente a esas tres circunferencias.
• Para hallar el centro de la circunferencia solución solo tienes que hacer las mediatrices de T₁ y T₂ por un lado y T₂ y T₃ por el otro. Donde esas mediatrices se cortan tienes O₂, el centro de la circunferencia solución.
• Para concluir, con centro en O₂ y radio hasta T₁, T₂ ó T₃, traza la circunferencia resultante.

Aquí abajo tienes una aplicación interactiva para que puedas entenderlo mejor. Puedes mover los centros A, B y C y de esa manera verificar la solución.

Otra posible solución

Este ejercicio tiene dos posibles soluciones, una circunferencia exterior y otra interior. La interior no es habitual pedirla, ya que por su pequeño tamaño suele ser muy complicada de dibujar. Por eso he optado por explicarlo aparte. También para no mezclar demasiadas lineas que dificulten la comprensión del ejercicio. La forma de resolverlo es igual que en el caso anterior, pero en esta ocasión, dibuja el centro de la circunferencia auxiliar alejándote de la circunferencia inicial. Mira abajo y lo entenderás.

Te puede interesar…

Ayúdame a mejorar esta entrada

¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti.

«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.