Tangencias sin conocer el radio de la solución

En este tipo de problemas conoces algunos elementos (rectas, circunferencias) y también algunos puntos concretos que pertenecen a la circunferencia buscada o que son puntos de tangencia con otro elemento. Son ejercicios bastante sencillos si recuerdas las propiedades de las tangencias. Los más comunes son:

Circunferencia tangente a una recta en un punto T y que pasa por un punto exterior P

Para este problema los elementos que conoces son una recta cualquiera a la que llamaremos r. Sobre esa recta conoces también un punto T que es el punto de tangencia sobre la recta de la circunferencia que te piden hallar. Por último, también conoces un punto exterior a la recta P que pertenece a la circunferencia solución. Así pues, tu punto de partida es parecido a esto.

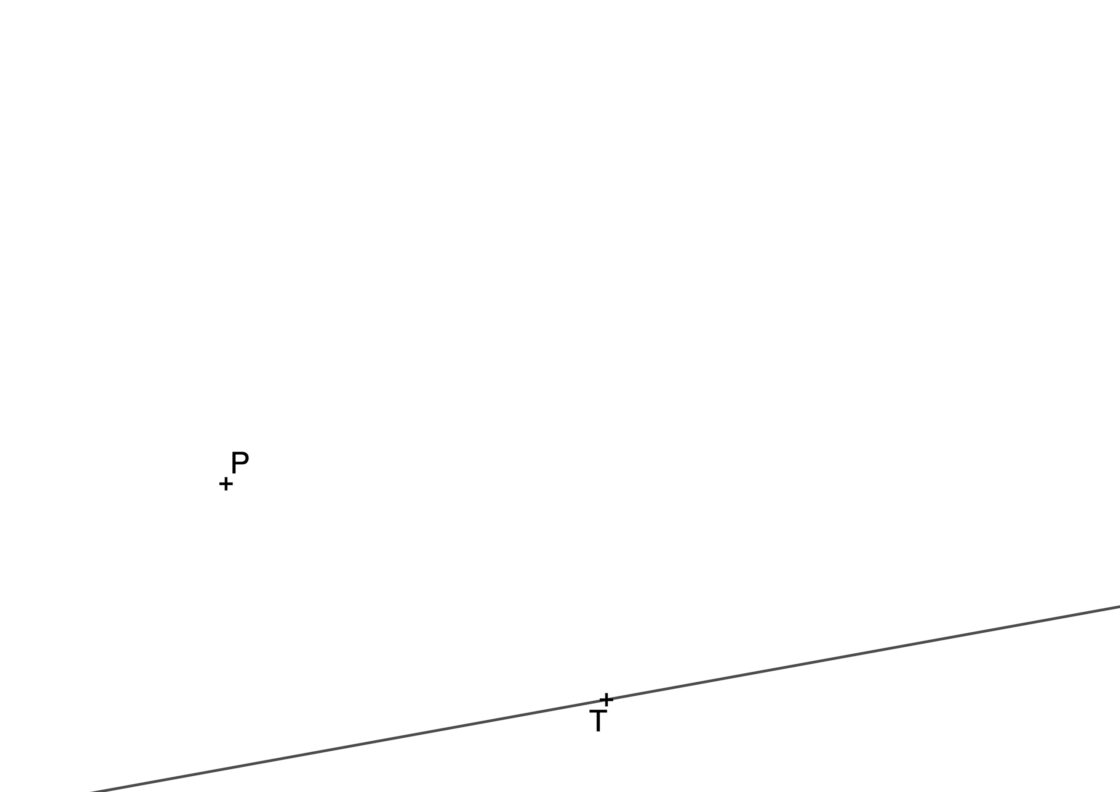
Este problema se resuelve recordando dos propiedades básicas de las tangencias. En primer lugar, cualquier circunferencia tangente a una recta tendrá su centro sobre una perpendicular a dicha recta que pase por el punto de tangencia. Así pues, dibuja para empezar una perpendicular a la recta r que pase por el punto T.

En segundo lugar, date cuenta que tanto P como T pertenecen a la circunferencia solución. Por tanto, el segmento que forman P y T es una cuerda de esa circunferencia. La otra propiedad que viene al caso es que si dibujamos la mediatriz de una cuerda de una circunferencia, dicha mediatriz siempre contendrá al centro. Dicho esto, dibuja la mediatriz del segmento que forman P y T.

El punto donde se cruzan la perpendicular que dibujaste al principio, y la mediatriz que acabas de dibujar, es el único lugar del plano que cumple ambas propiedades. Ese punto, por tanto, es O₁ el centro de la circunferencia buscada. Para terminar, pincha con el compás en O₁ y con radio hasta P ó T, dibuja la circunferencia solución.

En la aplicación interactiva de aquí abajo puedes mover los puntos azules para comprobar que el centro siempre está sobre la mediatriz y la perpendicular al mismo tiempo.

Circunferencias tangentes a tres rectas que se cortan

Cuando te piden resolver problemas de este tipo conoces tres rectas que se cortan entre si. En un principio tendrás cuatro circunferencias como parte de la solución. Una de ellas se encontrará en el interior del triángulo que forman las tres rectas, y las otras tres estarán fuera, en cada uno de los espacios determinados por tres rectas. Para los espacios determinados por dos rectas hay infinitas soluciones a menos que conozcamos un punto de tangencia, por lo que los vamos a ignorar.

Solo debes recordar una propiedad de las tangencias en éste caso. Cuando una circunferencia es tangente a dos rectas, su centro se encuentra sobre la bisectriz que forman dichas rectas. Como te decía antes, hay infinitas circunferencias tangentes a dos rectas, pero cuando añadimos una tercera recta la cosa cambia. En éste caso, la intersección de las bisectrices determinará un punto que será el centro. Para que sea más fácil dibujarlo, te he preparado dos láminas distintas. Una de ellas para la circunferencia interior, y otra para las tres exteriores, que será como si hiciéramos zoom. Vamos a empezar por la circunferencia central. Tu punto de partida será pues el siguiente:

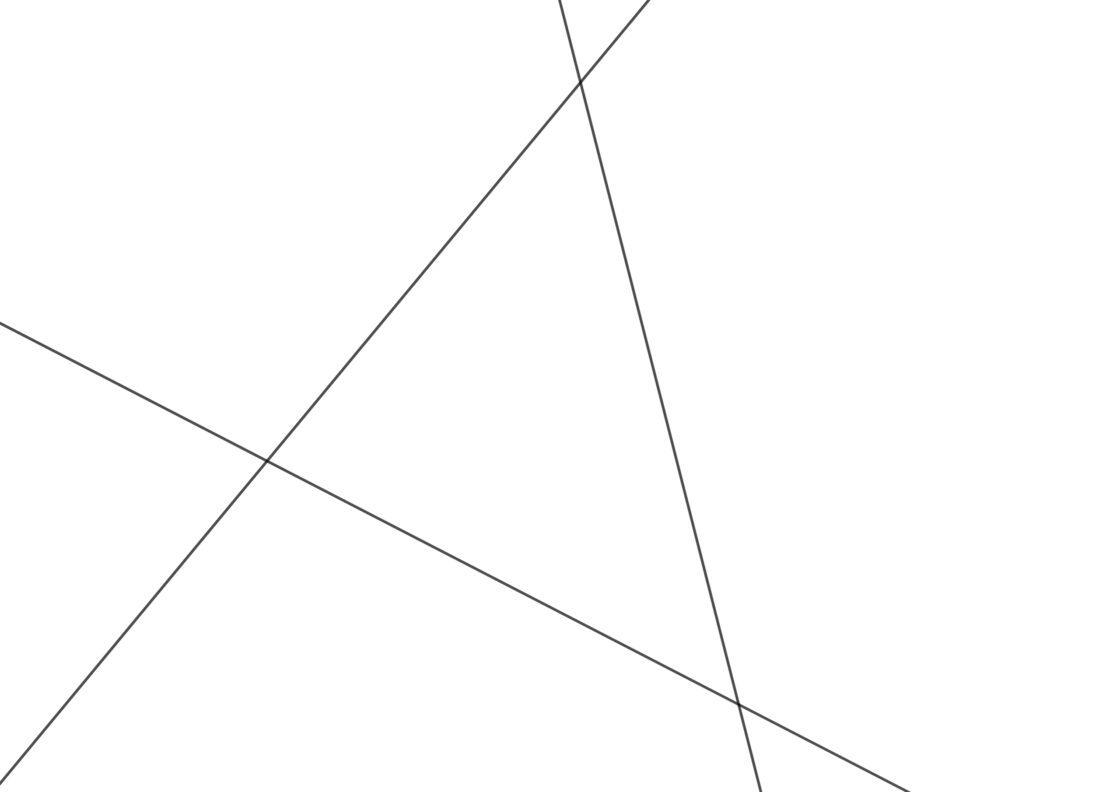
No es necesario que halles la bisectriz de los tres ángulos, con que traces las bisectrices de dos de ellos es suficiente. Así obtienes O₁, el centro de la primera circunferencia. Si haces una perpendicular a cualquiera de las tres rectas que pase por O₁, tienes en el corte T₁, y con centro en O₁ y radio hasta T₁ puedes dibujar la primera circunferencia. Por cierto, O₁ es además el incentro del triángulo que forman las tres rectas.

Para hallar las otras tres, solo tienes que dibujar las bisectrices de los ángulos que forman las tres rectas. Ten en cuenta que no tienen porqué ser tangentes a la circunferencia interior. Esto solo pasará cuando las tres rectas formen un triángulo equilátero. En el caso de un triángulo isósceles, la circunferencia exterior a la base también sería tangente a la interior. Para esta segunda parte del ejercicio puedes usar la siguiente lámina:

Para resolverlo, solo debes trazar las bisectrices que forman las rectas en la parte exterior del triángulo. En la aplicación interactiva de aquí abajo puedes mover los puntos azules para verificar que siempre se cumple la construcción, de manera independiente a la posición de las tres rectas.

No intentes hallar las circunferencias tangentes a los ángulos delimitados por solo dos rectas. Eso es imposible a menos que conozcas el radio de la solución. Date cuenta de que al ser solo dos líneas, el número de soluciones que puedes hallar es infinito. Para que lo entiendas, aquí abajo tienes el mismo ejercicio que arriba, pero un poco simplificado. Te he dejado un punto que puedes mover, el centro de la circunferencia O5. Como puedes comprobar, tienes una solución distinta para cada tamaño de circunferencia, y puedes marcar cualquier tamaño.

Circunferencias tangentes a dos rectas conociendo el punto de tangencia sobre una recta

Date cuenta de que en este tipo de ejercicios, a menos que te proporcionen un punto de tangencia, habría infinitas soluciones posibles. Para resolverlo debes recordar las propiedades de las tangencias. En primer lugar, recuerda que toda circunferencia tangente a dos rectas tendrá el centro sobre la bisectriz del ángulo. Lo segundo que debes recordar es que si una circunferencia es tangente a una recta, el centro estará sobre la perpendicular a la recta que pase por el punto de tangencia. Vamos a ver como se resuelve. Tu punto de partida es parecido a esto:

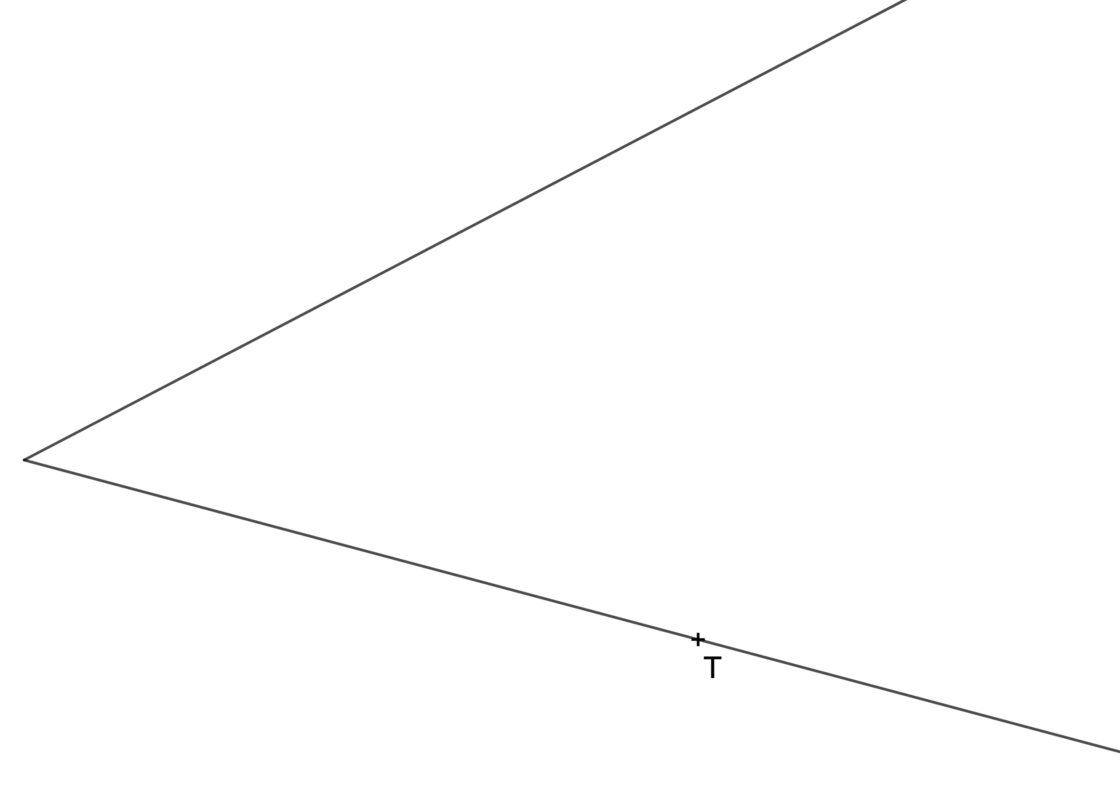
1. Empieza por dibujar una perpendicular a la recta por el punto de tangencia T.
2. Ahora traza la bisectriz del ángulo que forman ambas rectas.
3. El punto de corte de ambas rectas es el punto O, centro de la circunferencia que buscas.
4. Usando el compás, pincha en O y abre hasta T. Así podrás dibujar la circunferencia que te piden.

Circunferencia tangente a una circunferencia conociendo el punto de tangencia y un punto P exterior de la misma

En este caso lo que conoces es una circunferencia de centro O₁ y un punto P que no pertenece a la misma. También conoces el punto de tangencia T sobre la circunferencia. Lo que se te pide es dibujar una circunferencia tangente a la circunferencia inicial por el punto T y que además pase por P. En este caso las propiedades que debes recordar son:

• Dos circunferencias tangentes entre si, siempre tienen los centros alineados con el punto de tangencia.
• En cualquier cuerda de una circunferencia, el centro de la circunferencia está contenido en la mediatriz.

Tu punto de partida será parecido a esto:

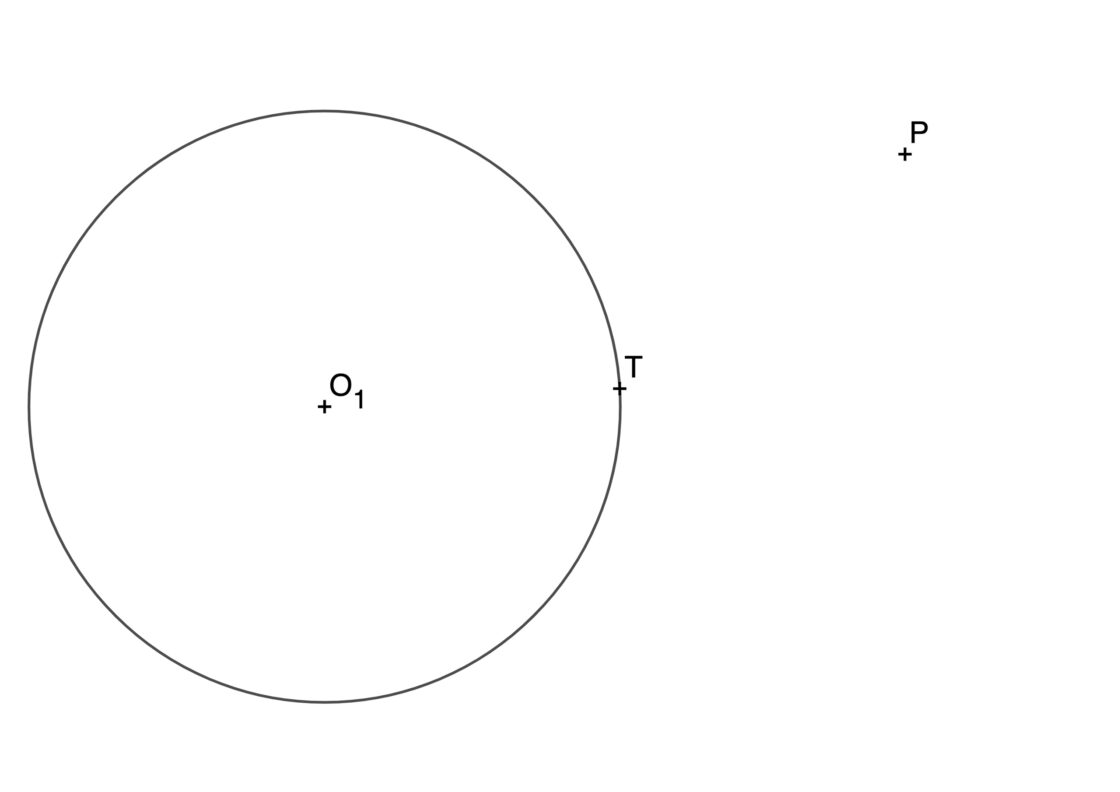
1. Empieza dibujando una línea que pase por O₁ y T, ya que sobre ella estará el centro de la otra circunferencia.
2. Ahora une T y P con un segmento, y halla la mediatríz de ese segmento. Recuerda que T y P forman parte de la circunferencia solución, por tanto son una cuerda de la misma.
3. El lugar donde la mediatríz y la recta que une O₁ y T se cortan es el centro O₂ de la circunferencia tangente.
4. Para terminar, con centro en O₂ y radio hasta T, dibuja la circunferencia que buscas.

Ten en cuenta que se puede dar el caso de que la circunferencia resultante contenga a la circunferencia inicial.

Circunferencia tangente a una recta y una circunferencia conociendo los puntos de tangencia

Para este problema te proporcionan los dos puntos de tangencia. Sobre la recta tienes T₁ y sobre la circunferencia tienes T₂. En este caso las propiedades que te interesan son:

• Una circunferencia tangente a una recta, siempre tendrá el centro sobre una perpendicular a la recta por el punto de tangencia.
• Dos circunferencias tangentes entre si, siempre tendrán los centros alineados con respecto al punto de tangencia.

Para este problema, el punto de partida será parecido a lo siguiente:

1. Dibuja una perpendicular a la recta que pase por el punto T₁ ya que sobre esa perpendicular estará el centro de la circunferencia que buscas.
2. Por otra parte, dibuja una línea que una T₂ y O₁, ya que sobre esa línea también estará el centro.
3. El punto donde ambas líneas se cortan es O₂, que es el único punto del plano que se encuentra al mismo tiempo sobre la perpendicular y sobre la recta que une O₁ y T₂. Ese punto es por tanto, el centro de la circunferencia solución.
4. Para terminar, con centro en O₂ y radio hasta T₁, dibuja una circunferencia. Esa es la circunferencia tangente a la recta y la circunferencia inicial con los puntos de tangencia que conocías.

Trazado de N circunferencias tangentes entre si, internas y externas a una circunferencia

Este método es de cosecha propia. No lo he visto escrito en ningún sitio. En el libro de Primero de Bachillerato de la Editorial Paraninfo viene un método para realizar éste ejercicio, pero solo es válido para 6 circunferencias. Este método vale para cualquier número de circunferencias.

El punto de partida es una circunferencia dada, y nos piden dibujar N circunferencias interiores y exteriores que sean tangentes entre si, y a la circunferencia. Para empezar, como puedes adivinar, las circunferencias serán iguales. Eso te permite deducir que el primer paso será dividir la circunferencia en N partes. En cada una de esas partes tendrás una circunferencia. Para este ejemplo vamos a dibujar cinco circunferencias tangentes entre si. Lo voy a dividir en dos ejercicios distintos, para que sea más fácil. En el primero de ellos vamos a dibujar cinco circunferencias tangentes entre si e internas a la circunferencia.

El primer paso es dibujar el polígono correspondiente dentro de esa circunferencia. En este caso, un pentágono. No necesitas dibujar los lados, solo con marcar los vértices vale. Tu punto de partida será este:

Si no recuerdas como se dibuja un polígono en cuestión, puedes revisar, en éste enlace te explico como dibujar polígonos regulares. No me voy a extender en este punto, a continuación tendrás algo parecido a esto.

El siguiente paso es hallar una de las circunferencias interiores. En este caso vamos a tomar como referencia la de la sección que determinan H, F y el centro O.

1. Dibuja una recta tangente por I. De esa manera determinas el punto J.
2. Traza la bisectriz del ángulo que forman I, J y O. Donde esa bisectriz corta al segmento que va de O a I tienes O₁, que es el primer centro.
3. Con centro en O₁ y radio hasta I puedes dibujar la primera circunferencia.
4. Dibuja los radios que unen O con B, D, y E, si no los habías dibujado antes.
5. Traza una circunferencia con centro en O y radio hasta O₁. Sobre esa circunferencia estarán los centros de todas las circunferencias que buscas.
6. Traza perpendiculares a los radios OH y OF que pasen por O₁. Donde esas perpendiculares cortan a la circunferencia que dibujaste antes, tienes los centros O₂ y O₃. Además, donde cortan a los radios OH y OF tienes los puntos de tangencia.
7. Con centro en O₂ y O₃ y radio O₁ hasta I puedes dibujar estas dos circunferencias.
8. Traza perpendiculares a los radios OE y OD que pasen por O₂ y O₃. De esa manera determinas O₄ y O₅.
9. Con el mismo radio de antes, y centro en O₄ y O₅, puedes dibujar las últimas dos circunferencias.

La segunda parte del ejercicio consiste en dibujar las circunferencias tangentes exteriores. El procedimiento es muy parecido al anterior. Para hacerlo más fácil, te voy a dejar los radios iniciales ya dibujados. Tu punto de partida será algo parecido a lo que ves aquí.

1. Empieza prolongando uno de los radios, en este caso utilizaremos el radio OA. Donde esa prolongación corta a la circunferencia tienes el punto F. Prolóngala más, ya que sobre ella estará el centro de una de las circunferencias.
2. Dibuja ahora una recta tangente a la circunferencia que pase por F.
3. Luego traza la bisectriz de un ángulo que formen esa recta que acabas de dibujar con uno de los radios que ya tienes dibujado. Por ejemplo OJ. Esa bisectriz corta a la prolongación de OF en O₁, que es el centro de la primera circunferencia.
4. Una vez tienes ese centro, debes trazar una circunferencia con centro O y radio hasta O₁. Sobre esa circunferencia marcaremos más adelante los centros de todas las circunferencias tangentes.
5. Dibuja perpendiculares a los radios que pasen por O₁. Donde esas perpendiculares cortan a la circunferencia que acabas de dibujar tienes O₂ y O₃.
6. Luego realiza perpendiculares a los radios que pasen por O₂ y O₃ para hallar O₄ y O₅ de la misma manera.
7. Para terminar, con radio O1F dibuja las circunferencias de centro O₂, O₃, O₄ y O₅.

Y aquí abajo tienes lo que podría ser el resultado de combinar ambos ejercicios en uno solo.