Rectas límite en homología

En homología, las rectas límite se definen como el lugar geométrico de los puntos del plano cuyos puntos homólogos están en el infinito. Como en toda relación de homología hay dos figuras, siempre habrá dos rectas límite. En una homología podemos calcular el punto homólogo de un punto impropio, es decir, que se encuentra en el infinito. Las rectas límite son siempre paralelas al eje de homología.

A lo mejor este concepto te resulta un poco confuso. Para aclararlo te he preparado la siguiente aplicación interactiva. Puedes mover el centro O, y los puntos B y A’. Fíjate que pasa cuando B se acerca a la recta l. El punto B’ se aleja hacia el infinito. Por otra parte, si mueves el punto A’ en dirección a la recta l’, el punto A se va al infinito.

Hallar las rectas límite dadas dos rectas homólogas r y r’, el eje y el centro de homología

Para este problema conoces el centro de homología, representado por el punto O. También conoces el eje de homología y un par de rectas homólogas r y r’ (las rectas azules). El procedimiento para hallar las rectas límite es muy sencillo. El punto de partida será algo similar a esto:

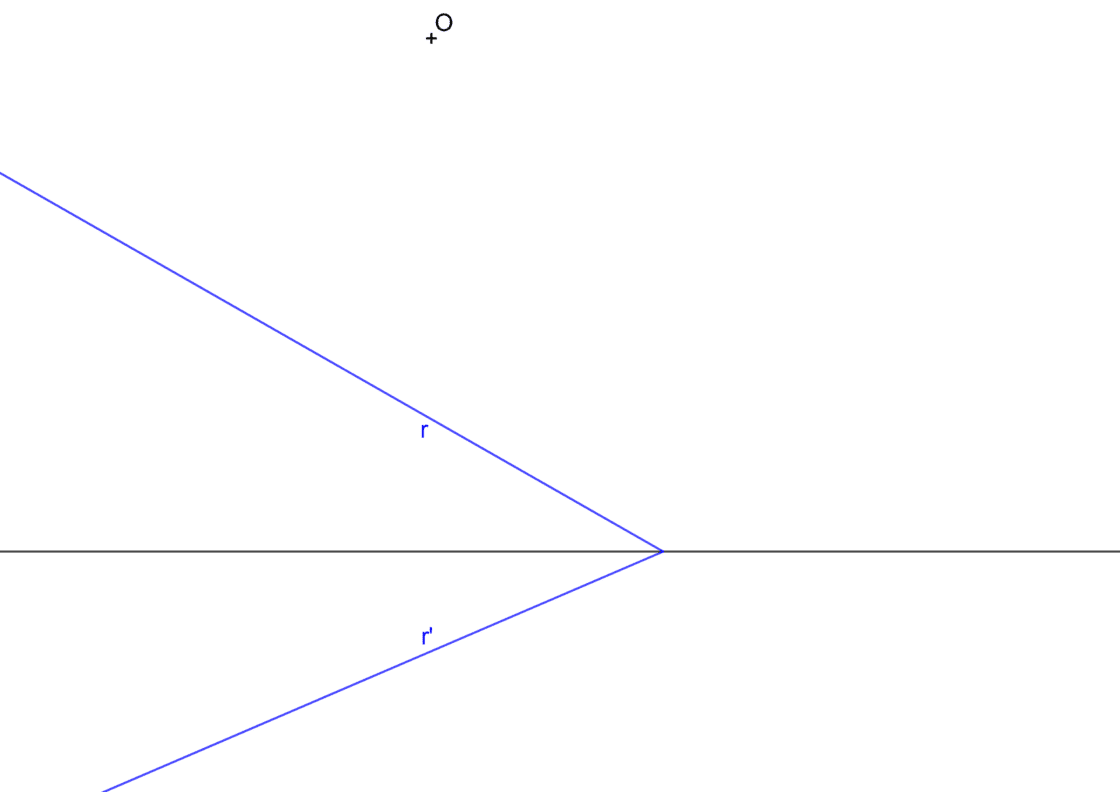
1. Dibuja una recta paralela a la recta r’ que pase por O. Donde esta paralela corta a la recta r tienes el punto P, que se encuentra en el infinito, por tanto sobre una recta límite.
2. Traza una línea que sea paralela al eje y que pase por P. Esa es la primera recta límite.
3. Ahora marca una línea paralela a la recta r y que pasa por O. Donde esa línea corta a la prolongación de la recta r’ tienes el punto P’, que te permite dibujar la segunda recta límite.

En la aplicación de aquí abajo puedes mover los puntos A y B para cambiar la posición de las rectas r y r’. También puedes mover el centro de homología O y el punto S, que determina la posición del eje de homología.

Dibujar la figura homóloga al triángulo ABC conociendo el eje, el centro O y la recta límite l

En este caso no conoce el homólogo de ningún punto. Lo que conoces es el centro de homología, el eje y una recta límite. Y por supuesto, la figura de la cual debes hallar su homóloga. En este caso se trata del triángulo ABC. Así pues, tu punto de partida es algo similar a lo que ves a continuación.

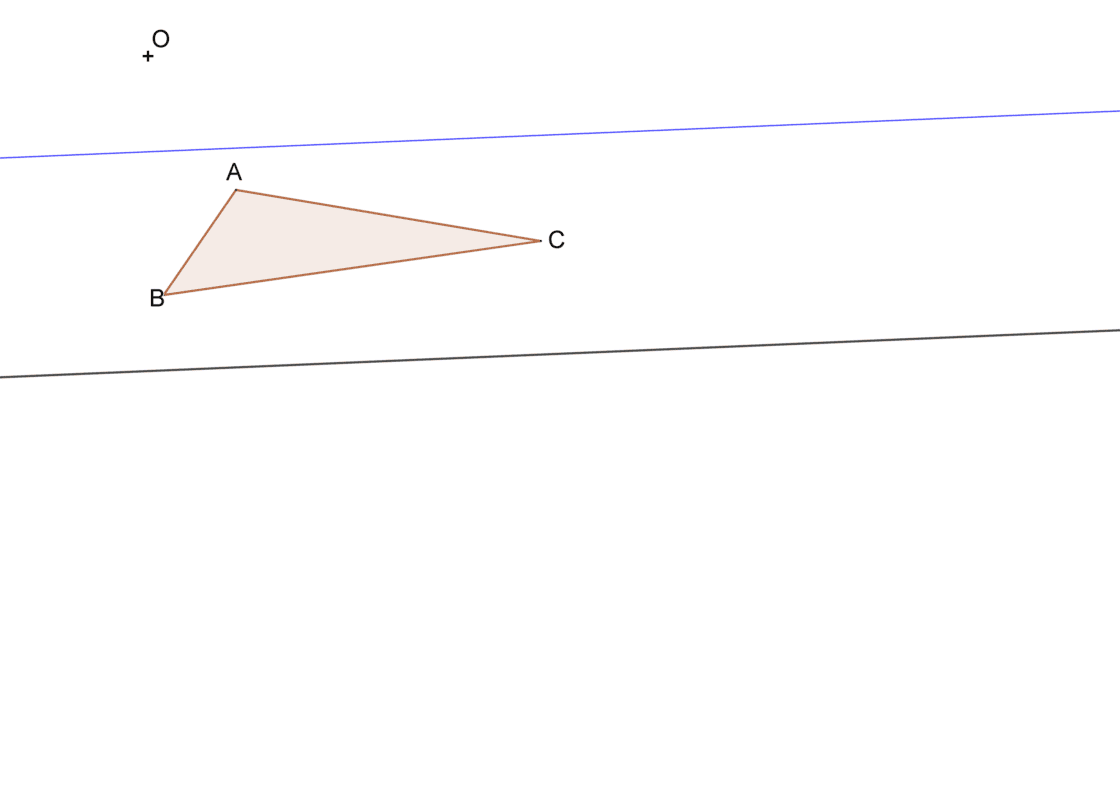
Para que te sea más fácil entender este ejercicio, puedes pulsar sobre la imagen de aquí arriba para abrirla a pantalla completa e imprimirla en un DIN A4. Para resolver este ejercicio debes entender una cosa de las rectas límite. Dado un par de rectas homólogas r y r’, si unes O con el punto de corte de r con la recta límite, esa recta que dibujas será siempre paralela a la recta r’. Aquí tienes una pequeña demostración.

Puedes mover los puntos A y B que definen la recta r, y el punto B’ que define la recta r’. También puedes mover el centro de homología O. Date cuenta de que por más que los muevas, el segmento que forman O y P siempre será paralelo a la recta r’. El punto R no forma parte de la construcción, lo puedes mover para verificar el paralelismo. Así pues, para resolverlo se procede de la siguiente manera:

1. Prolonga la recta que une A y B hasta cortar al eje en el punto D, y a la recta límite en el punto P.
2. Dibuja una recta paralela al segmento que forman OP y que pase por D.
3. Traza una línea que pase por O y por B, y prolóngala hasta cortar a esa paralela que acabas de dibujar. Donde esas dos rectas se cortan tienes el punto B’.
4. Si realizas una línea que pase por O y A y la prolongas hasta cortar a la misma paralela, tendrás el punto A’ en el lugar donde se cortan las dos.
5. Llegados a este punto, puedes resolver el resto del ejercicio de la forma habitual.

Hallar el centro de homología conociendo el eje, una recta límite y un par de puntos homólogos A-A’

Para resolver este ejercicio tienes que aplicar el mismo principio que usaste para el ejercicio anterior. Los datos que te proporcionan para poder resolver el ejercicio son el eje, una recta límite y un par de puntos homólogos A y A’. Tu punto de partida es algo similar a lo que ves a continuación.

Puedes pulsar sobre la imagen de aquí arriba para abrirla a pantalla completa. Luego puedes imprimirla en un DIN A4 para practicar este ejercicio.

1. Empieza por dibujar una recta cualquiera que pase por A. Esa recta corta a la recta límite en el punto L y al eje en el punto L’.
2. Dibuja la recta que une A’ con A y prolóngala un poco hacia arriba, ya que por allí estará el centro de homología.
3. Ahora traza una paralela al segmento que forman A y L’ que pase por L. Donde esa paralela corta a la recta que pasa por A y A’ tienes el punto O, que es el centro de la homología.

Aquí abajo puedes mover el punto L para cambiar la posición de la recta límite, con ello cambiarás también la posición tanto de O, como de A’. También puedes mover tanto A como A’, de esa manera también modificas la posición del centro de homología (pero no la recta límite ni el eje). Por último, también puedes mover el punto P para cambiar la posición del eje. Al hacerlo cambias O y A’, pero no la recta límite ni la posición de A. Fíjate que en cualquier caso, el segmento que forman L y O es siempre paralelo al segmento que forman A’ y L’.

Hallar el eje de homología conociendo el centro O y las rectas límite

Para este ejercicio conoces el centro de homología O y ambas rectas límite. Lo que se te pide es hallar el eje de homología. Como vas a comprobar enseguida, es muy similar a los ejercicios que tienes más arriba. Tu punto de partida es muy similar a lo que ves a continuación.

Ya sabes que puedes pulsar sobre la imagen de aquí arriba para abrirla a pantalla completa. De ese modo puedes imprimirla en un DIN A4 para poder practicar este ejercicio.

1. Dibuja una recta auxiliar cualquiera que pase por O. Donde esa recta corta a la primera recta límite tienes el punto L.
2. A continuación dibuja otra recta auxiliar cualquiera que pase por O (preferiblemente que forme un ángulo cercano a 90 grados con la primera). Donde esa recta corta a la otra recta límite tienes el punto L’
3. Realiza una recta paralela al segmento que forman L y O que pase por L’.
4. Ahora dibuja una recta paralela al segmento que forman O y L’ que pase por L.
5. Donde esas dos rectas paralelas que acabas de dibujar se cortan tienes el punto P.
6. El eje será la recta paralela a las rectas límite que pasa por P.

Aquí abajo puedes mover L y L’ para verificar que P siempre se encuentra sobre el eje. Da igual la posición que ocupen L y L’, la posición del eje no varía. También puedes mover el centro O de homología para ver como cambia la posición del eje.