Homología en dibujo técnico

La homología es una transformación geométrica que cumple las siguientes propiedades:

• Todos los puntos originales y sus homólogos se encuentran alineados respecto de un punto que se denomina centro de homología.
• Dos rectas homólogas se cortan siempre en una recta a la que se llama eje de homología.
• El eje de homología es el lugar geométrico de los puntos del plano que son homólogos de si mismos (razón doble de homología).

Aquí abajo te dejo una aplicación sencilla para poder comprender las propiedades de este tipo de transformaciones. Puedes mover los puntos A y A’ para modificar el par de rectas homólogas r y r’. También puedes mover el punto O para modificar el centro de homología. Puedes mover asimismo los puntos P y R para modificar el eje. Por último, puedes mover el punto B para ver cómo se comporta su punto homólogo B’.

Problema sencillo de homología: Triángulo

Este es un ejercicio muy básico que te puede ayudar a entender como funciona una relación geométrica homológica. Los elementos que conoces son la figura original, formada por el triángulo ABC, el eje y el centro de homología y A’, homólogo del punto A. Tu punto de partida se parece a ésto:

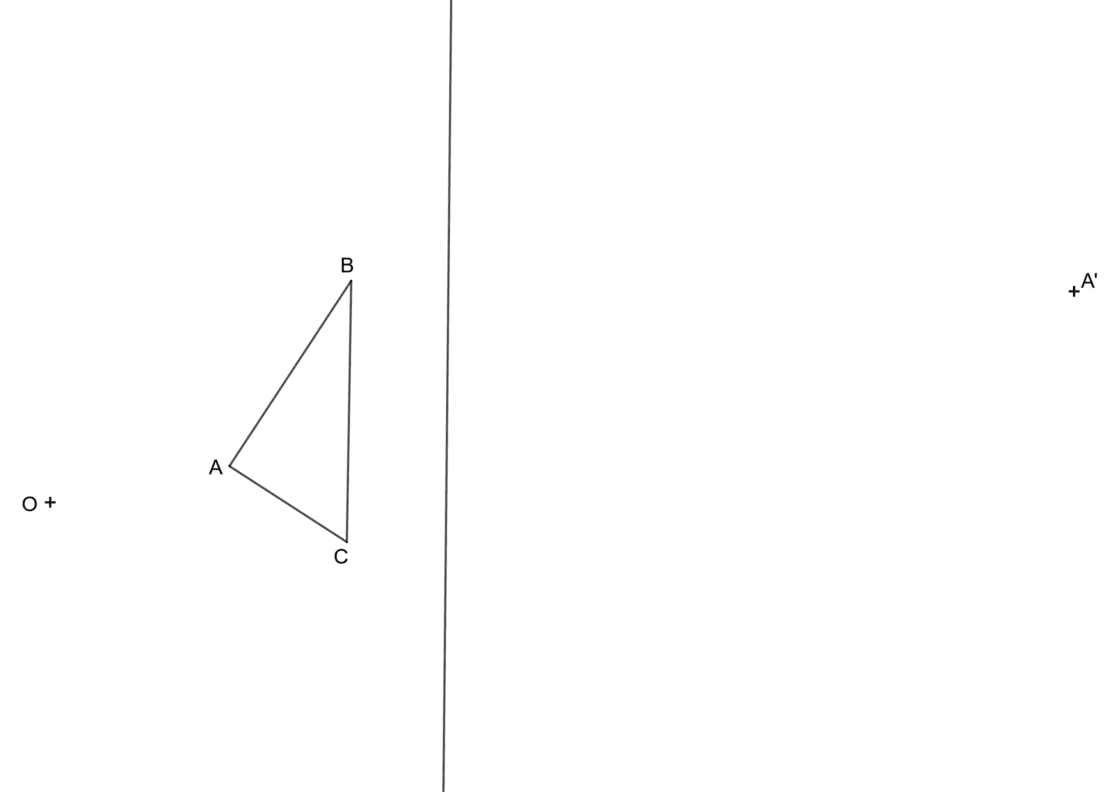
En éste tipo de problemas, sobretodo si se trata de ejercicios más complejos, recomiendo ir punto por punto. No es recomendable dibujar todos los haces proyectantes en primer lugar, porque te puedes confundir fácilmente. Por otra parte, tampoco recomiendo dibujar las líneas enteras. Ten en cuenta que a mi no me queda otra porque el programa con el que trabajo funciona así, pero yo recomiendo dibujar solo el principio de la línea, el punto de intersección y el final de la línea. De ese modo es más fácil ver donde se cortan las líneas y evitas equivocarte.

Dicho esto… ¡Vamos a resolverlo!

• En primer lugar, prolonga el segmento que forman A y B hasta cortar al eje en el punto P.
• Une P con A’. Date cuenta de que el segmento PA’ es homólogo del segmento AP, por tanto B’ estará en algún lugar entre P y A’
• Dibuja la línea que pasa por O y B y prolóngala hasta cortar al segmento que forman P y A’. El punto de corte es B’.
• Ahora prolonga el segmento que forman A y C hasta cortar al eje en el punto R. Si unes R con A’ verás que este segmento es homólogo del que forman A y R.
• Traza la línea que pasa por O y C y prolóngala hasta cortar al segmento RA’. El punto donde se corten será C’
• Para finalizar solo tienes que unir A’, B’ y C’ y ya tienes el triángulo homólogo del triángulo original ABC.

Como ves, es una construcción bastante sencilla, aquí abajo tienes la solución en una aplicación interactiva. Puedes mover el centro de homología O, los tres puntos del triángulo inicial y A’ para ver como se comporta la construcción.

En el siguiente vídeo tienes todo el proceso desarrollado y explicado para que puedas verlo paso por paso.

Como dibujar la elipse homóloga a una circunferencia

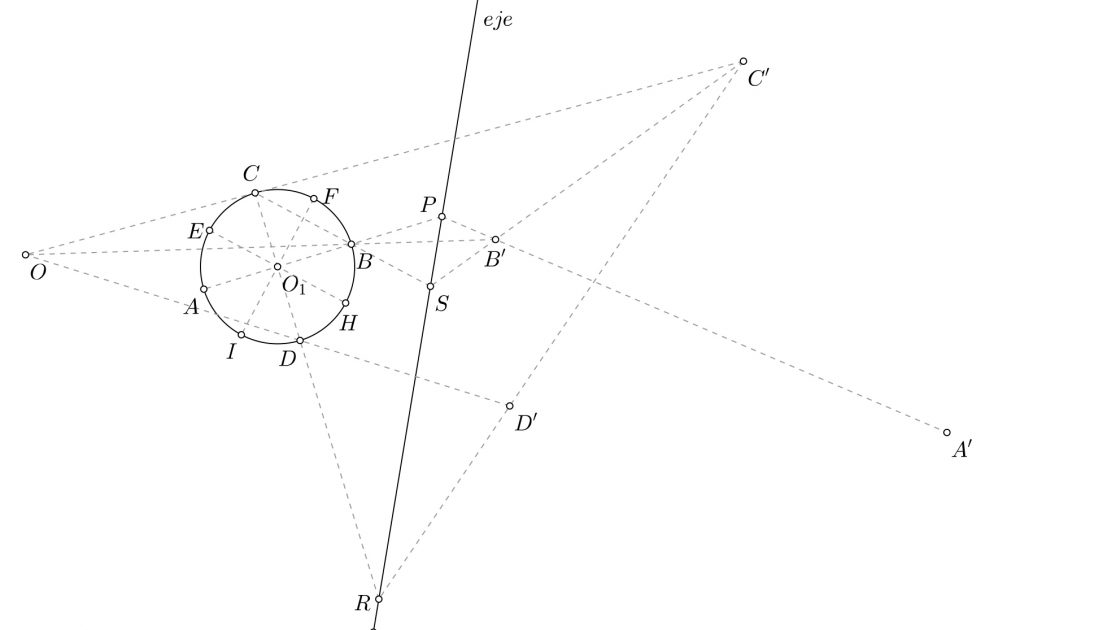
Este problema es un poco más complejo que el anterior. En éste caso vas a ver como dibujar la figura homóloga a una circunferencia (siempre es una elipse), cuando conoces el eje y el centro de homología y un par de puntos homólogos A y A’. Tu punto de partida será semejante a éste:

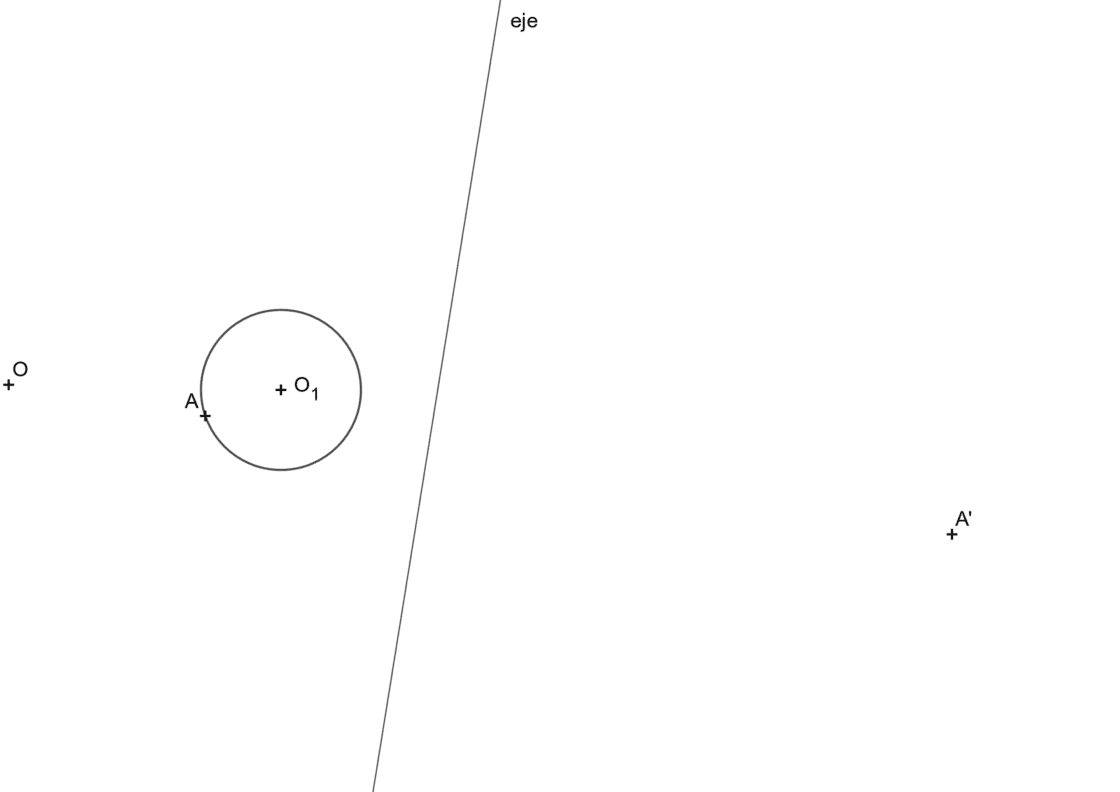
Un consejo adicional a todos los que te daba en el paso anterior… Si esta construcción la encuentras realmente compleja, pero se te da bien dibujar formas sencillas como triángulos o cuadrados, puedes imaginar que la circunferencia está formada por dos cuadrados cruzados. Al fin y al cabo, lo que te interesa son los puntos.

Dicho ésto… !!!vamos a por ello!!!

• Como siempre digo, lo mejor es hallar los puntos uno por uno. De ese modo evitarás liarte. Empieza por dibujar una línea que pasa por A y el centro de la circunferencia. Prolonga esa línea de modo que corte en el eje en el punto P y en la circunferencia en el punto B. En caso de que no te resulte cómodo hallar B, puedes hacer una perpendicular al segmento AB y hallar C y D en los puntos de corte con la circunferencia, igual que si fuera un cuadrado.
• Dibuja una línea que pase por O y por B, en su prolongación corta al segmento que forman P y A’ en el punto B’.

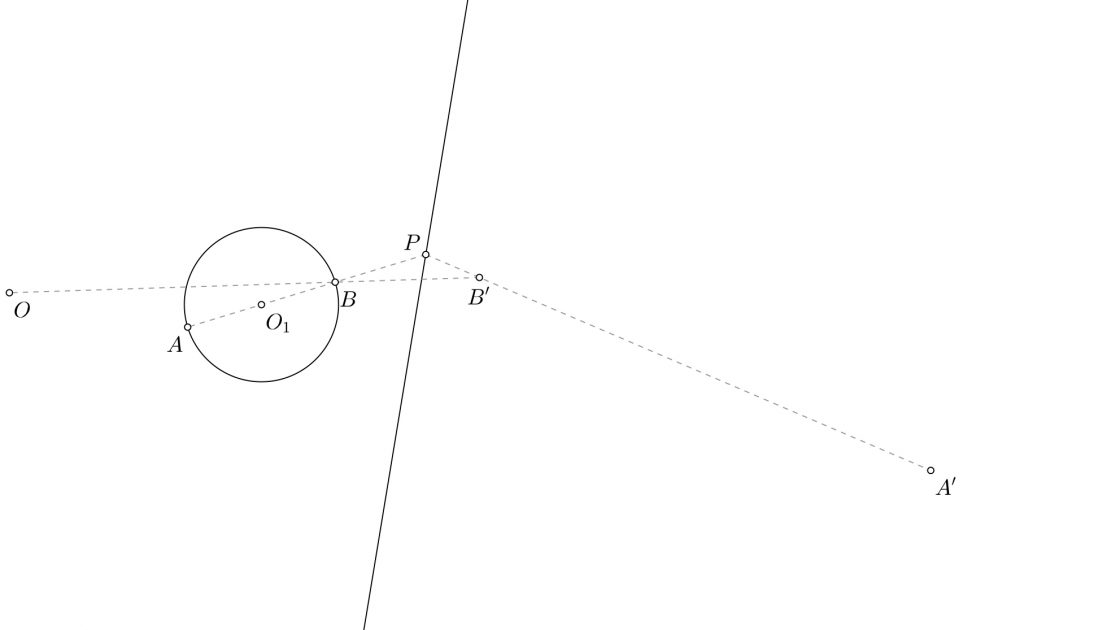
He querido ponerte la imagen de éste primer paso porque todos los demás puntos se hallan de manera parecida. Si entiendes como acabas de hallar B’, no tendrás problema con los demás. Si no lo entiendes, te recomiendo ver el ejercicio anterior antes de intentar hacer este.

• El siguiente paso consiste en hacer una perpendicular al segmento AB. Esta perpendicular corta en dos puntos, C y D, que serán los siguientes que vamos a hallar. Puedes prolongar esta perpendicular hasta cortar al eje en R, que utilizaremos más tarde.
• Ahora dibuja la línea que une C con B y prolóngala hasta cortar al eje en el punto S.
• Lo siguiente que debes trazar, es la línea que pasa por O y C, y prolongarla bastante.
• Dibuja la recta que pasa por S y B’, en su prolongación corta a la recta anterior en el punto C’

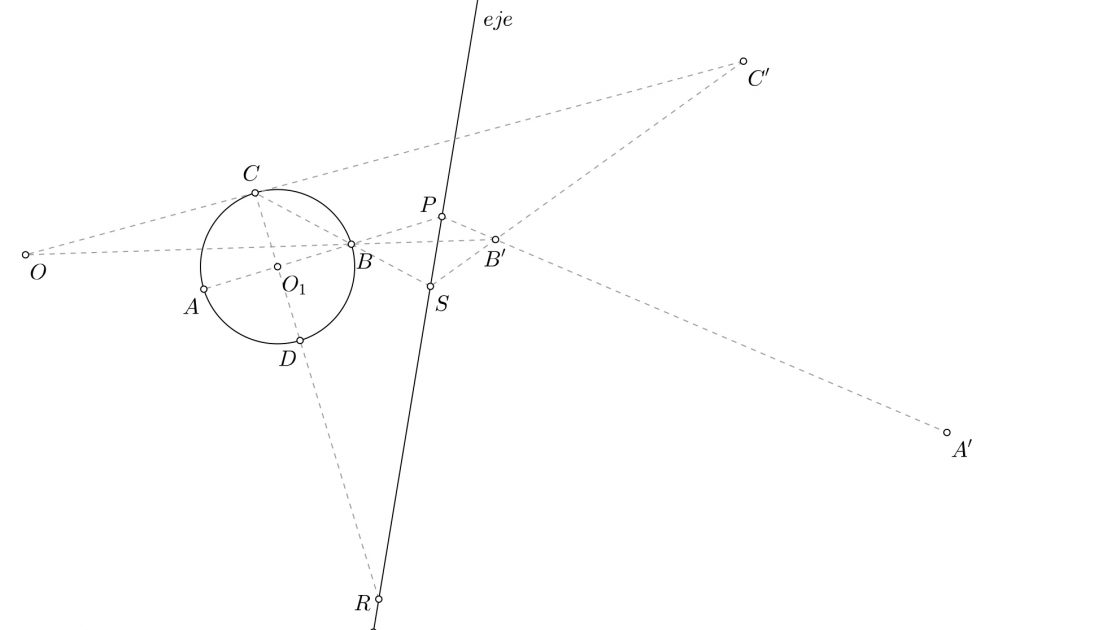
• Ahora que tenemos el punto C’, podemos usarlo para hallar el punto D’. Para ello dibuja la línea que une el punto R con C’.
• Dibuja una línea que pase por O y por D, y prolóngala hasta cortar a la línea anterior. El punto donde se cortan ambos segmentos es el punto D’. Con esto ya tienes la mitad del ejercicio resuelto.
• El siguiente paso será hallar los puntos intermedios entre los puntos A, B, C y D en la circunferencia. Para ello debes dibujar las bisectrices de los ángulos que forman. De esa forma obtienes los puntos E, F, H e I.

Para hallar los homólogos de E, F, H e I, debes relacionarlos con un par de puntos que si conozcas. Llegados a este punto es sencillo, porque puedes utilizar A, B, C ó D. El primero que voy a marcar yo será F’.

• Traza una línea que pase por F y B. Esa línea corta al eje en el punto T.
• Une T con B’ y prolónga esa línea un poco.
• Dibuja la línea que pasa por O y por F y prolóngala hasta cortar al segmento que dibujaste ante. El punto de corte será F’.
• Gracias a F’ puedes ubicar H’. Para ello dibuja la línea que une F con H y alárgala hasta cortar al eje en el punto V.
• Une V con F’.
• Ahora dibuja la línea que pasa por O y por F y prolóngala hasta cortar al segmento que forman V y F’. El punto donde cortan esas líneas es H’.

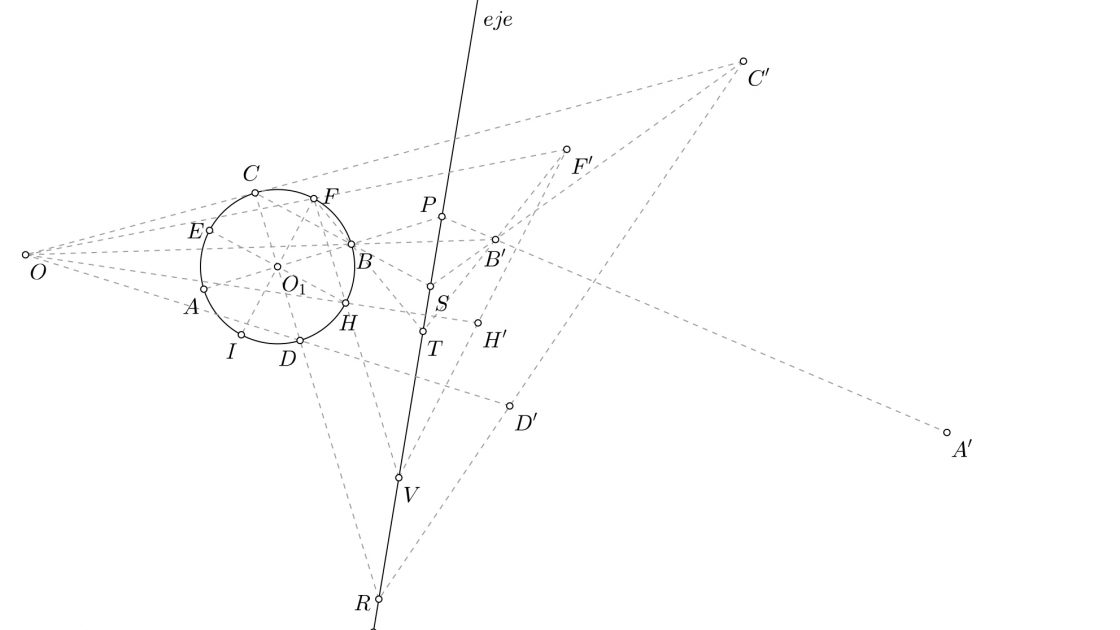
Ya casi has acabado, solo faltan dos puntos más. Puedes utilizar cualquiera de los anteriores para hallarlos. Yo voy a continuar con el punto I, aprovechando el punto original A y A’.

• Para ello dibuja la línea que pasa tanto por A como por I y llévala hasta cortar al eje en el punto W.
• Ahora une el punto W que acabas de hallar con A.
• Lo siguiente que debes hacer es dibujar la línea que pasa por O y por I y prolongarla hasta cortar al segmento anterior RA’. El punto donde se cortan ambas líneas es I’.
• El último punto que tienes que hallar es E’. Para ello puedes utilizar cualquier punto. Yo en éste ejemplo voy a usar el punto C. Así pues, dibuja la recta que une C y E, alargándola hasta cortar al eje en el punto Y.
• Une Y con C y continúa esa línea bastante.
• Para terminar dibuja la línea que pasa por O y por E y síguela hasta cortar con la línea que dibujaste antes. Ese punto de intersección es E’.
• Para terminar, utiliza la plantilla de curvas para dibujar la elipse.

Aquí abajo tienes una aplicación interactiva con el resultado. Puedes mover los puntos O₁, A y A’ para modificar la circunferencia y la elipse resultante. También puedes mover los puntos O, R e Y para modificar el eje y el centro de homología. De esa manera puedes ver como se comporta la elipse resultante y los pares de puntos homólogos. Te recomiendo ponerlo a pantalla completa para verlo mejor. También puedes ir haciendo zoom sobre cada zona si alguna parte no te queda clara para ver como se calculan las intersecciones de los puntos.

Hallar el homólogo de un punto conociendo dos parejas de puntos homólogos y la dirección del eje

En éste caso no se conoce el eje, tan solo la dirección que sigue. También conoces dos parejas de puntos homólogos A-A’ y B-B’. Otro inconveniente de este problema es que tampoco conoces el centro de homología. Es decir, tu punto de partida debe ser algo semejante a lo que ves a continuación.

Puedes pulsar sobre la imagen para que se abra a pantalla completa y de esa forma imprimirla en un DIN A4 para practicar. Para resolver este ejercicio tienes que recordar que dos rectas afines tienen un punto común en el eje, ya que todos los puntos del eje son homólogos de si mismos. Además, recuerda que todas las rectas que pasan por un par de puntos homólogos parten siempre del centro de homología. Dicho esto…

1. Traza líneas que pasen por P y P’ por un lado, y por R y R’ por el otro. Donde esas rectas se unen tienes el centro de homología O.
2. Ahora traza rectas que pasen por P y R por un lado, y por P’ y R’ por el otro. Donde esas rectas se cruzan tienes el punto T, que es homólogo de si mismo. Esto significa que se encuentra sobre el eje. Así pues, para dibujar el eje solo tienes que hacer una paralela a la dirección que te indican y que pase por el punto T.
3. Llegados a este punto, puedes resolver el ejercicio de la forma habitual.