Los óvalos son curvas técnicas, formadas por cuatro arcos de circunferencia, iguales dos a dos. Son simétricos respecto a dos ejes perpendiculares entre si a los que se denominan eje mayor y eje menor. Su uso más importante lo podemos encontrar en el dibujo de perspectivas, ya que permite sustituir elipses de forma rápida y aproximada. Estos métodos son precisos, y se basan en las propiedades de las tangencias. Si te acuerdas de ellas, podrás resolver parte de estos ejercicios por deducción.
Óvalo conocido el eje mayor (procedimiento 1)
Hay dos maneras habituales de dibujar un óvalo a partir de su eje mayor. En los siguientes ejercicios el eje mayor está representado por el segmento AB. Tanto para el primer caso, como para el segundo, tu punto de partida será algo parecido a esto:

Te explico el primer procedimiento:
- Empieza por dividir el eje mayor el tres partes usando el teorema de Tales. Los puntos intermedios son O1 y O2, el centro de los dos arcos laterales.
- Con centro en O1 y radio hasta A dibuja una circunferencia.
- Lo siguiente es trazar otra circunferencia, con centro en O2 y radio hasta B.
- Los puntos donde ambas circunferencias se cortan son O3 y O4, centros de las circunferencias que contienen a los arcos superior e inferior.
- Dibuja líneas que pasen por O1 con O3 y por O1 con O3.
- Continúa trazando líneas que pasen por O2 y O3 por un lado y por O2 y O4 por el otro.
- Donde esas líneas cortan a las circunferencias de centro O1 y O2 que dibujaste antes tienes los puntos T1, T2, T3 y T4. Esos son los puntos de tangencia donde se cambia de un arco a otro.
- Con centro en O1 y radio hasta T1 dibuja un arco de T1 hasta T4.
- Ahora dibuja un arco con centro en O3 y radio hasta T4 que vaya de T4 a T3.
- A continuación dibuja un arco con centro en O2 y radio hasta T3 que vaya de T3 hasta T2.
- Para terminar, dibuja un arco con centro en O4 y radio hasta T2 que vaya de T2 hasta T1.
Aquí abajo tienes un vídeo explicativo de éste procedimiento, por si tuvieras alguna duda.
Óvalos conocido el eje mayor (procedimiento 2)
Este segundo procedimiento te permite hallar óvalos un poco más achatados.
- Empieza por dividir el eje mayor en cuatro partes iguales usando el teorema de Tales. Las partes que corresponden a los segmentos 2 y 4 son los centros O1 y O2.
- Con centro en O1 y radio hasta O2 dibuja un arco. Luego dibuja otro con centro en O2 y radio hasta O1 dibuja otro arco.
- Donde ambos arcos se cortan tienes los centros O3 y O4.
- Al igual que en el ejercicio anterior, dibuja líneas que pasen por O1 y O3 por un lado y por O1 y O4 por el otro.
- Luego dibuja líneas que pasen por O2 y O3 por un lado, y por O2 y O4 por el otro.
- Con centro en O1 y radio hasta T1 dibuja un arco que vaya de T1 a T4.
- A continuación dibuja un arco con centro en O4 y radio hasta T1 que vaya de T1 a T2.
- Luego dibuja otro arco con centro en O2 y radio hasta T2 que vaya de T2 a T3.
- Para finalizar dibuja un arco con centro en O3 y radio hasta T3 que vaya de T3 a T4.
Óvalos conocido el eje menor
Para este ejercicio conoces el tamaño del eje menor, representado en este caso por el segmento CD. De todas formas esta construcción tiene un pequeño truco, ya que C y D son al mismo tiempo los centros O1 y O2. Tu punto de partida será semejante a esto:
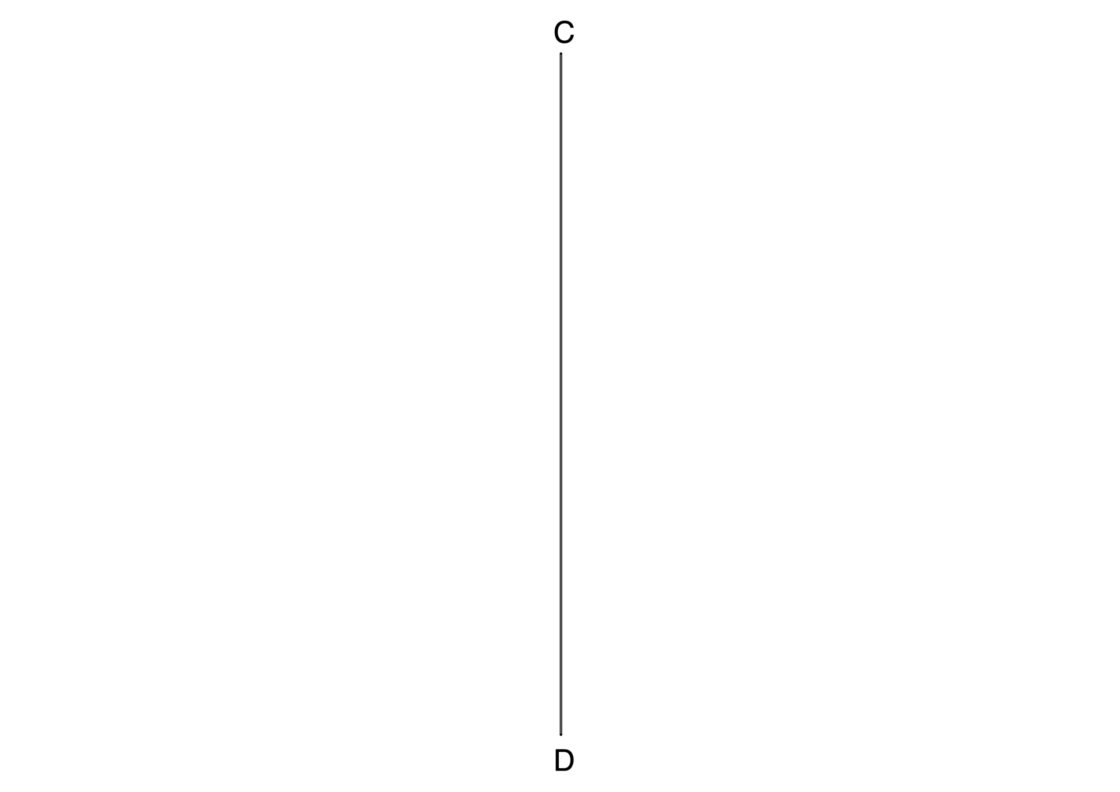
- Así pues empieza por dibujar la mediatriz del eje menor. Como ya sabes los óvalos son simétricos, de modo que sobre esa mediatriz se encontrará el eje mayor. Al punto donde la mediatriz y el eje menor se cruzan llámalo O. Ese es el centro del óvalo.
- Con centro en O y radio hasta O1 traza dos arcos que cortan a la mediatriz en los puntos O3 y O4, centro de las otras dos circunferencias que necesitas para completar este ejercicio.
- Con centro en O1 y radio hasta O2 dibuja un arco.
- Repite la operación dibujando un arco con centro en O2 y radio hasta O1.
- Ahora traza una línea que salga de O1 y pase por O3 y otra que salga de O1 y pase por O4.
- Luego dibuja una línea que salga de O2 y pase por O3. También otra que salga de O2 y pase por O4.
- Donde estas líneas cortan a los arcos que dibujaste antes tienes los puntos T1, T2, T3 y T4. Estos son los puntos de tangencia donde los arcos cambian de centro.
- Dibuja un arco con centro en O1 y radio hasta T3 que vaya de T3 a T4.
- Con centro en O4 y radio hasta T4 dibuja un arco que vaya de T4 a T2.
- Ahora dibuja un arco con centro en O2 y radio hasta T2 que vaya de T2 a T1
- Para terminar, traza un arco con centro en O3 y radio hasta T1 que vaya de T1 a T3.
Aquí abajo tienes un vídeo explicativo donde puedes ver como se realiza este proceso paso a paso.
Óvalo inscrito en un rombo
Este ejercicio es muy interesante, ya que una variante del mismo se utiliza para dibujar círculos en perspectiva isométrica. Es lo que se denomina un óvalo isométrico. El procedimiento es realmente sencillo. Tu punto de partida es parecido a lo siguiente:
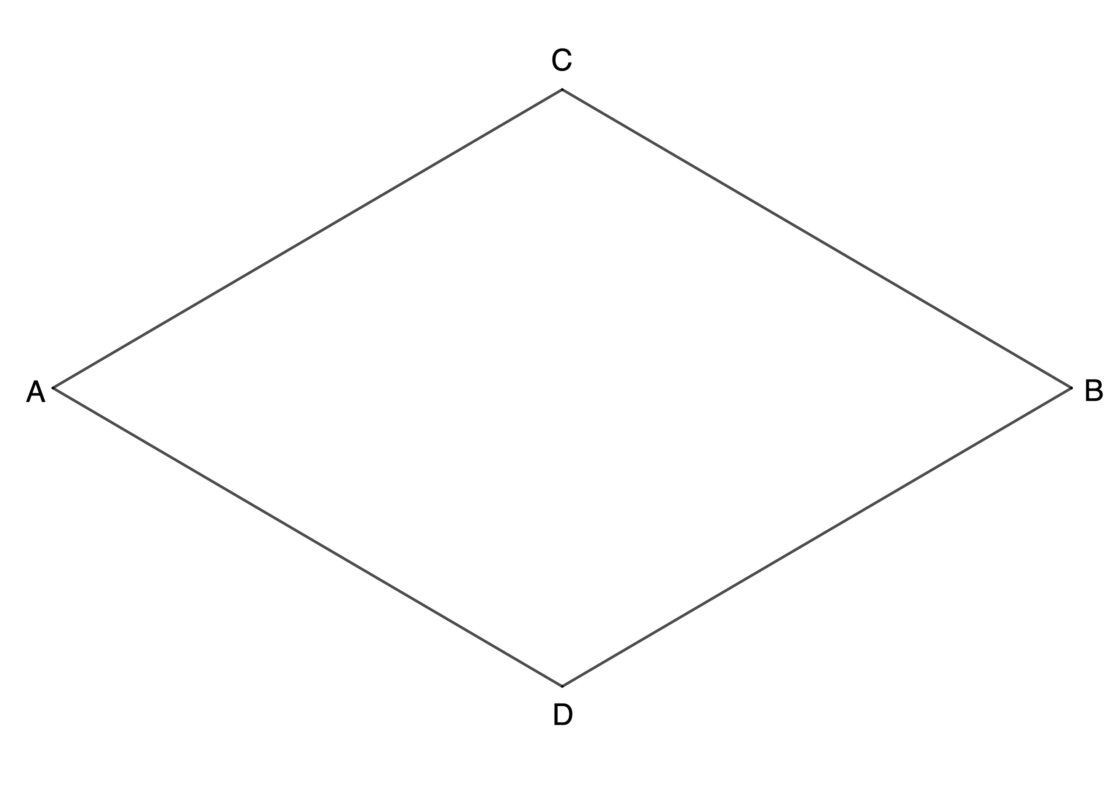
- Empieza renombrando los vértices superior e inferior. Llámalos O1 y O2, ya que son los centros de los arcos inferior y superior.
- Dibuja perpendiculares a los lados que pasen tanto por O1 como por O2. Los puntos donde esas perpendiculares cortan a los lados son T1, T2, T3, T4. Los puntos de tangencia donde se cambia de un arco a otro.
- Los puntos donde se cortan las rectas perpendiculares que dibujaste antes son O3 y O4, los dos centros de los arcos que te faltan.
- Con centro en O2 y radio hasta T1 dibuja un arco que vaya de T1 a T2.
- Ahora dibuja un arco con centro en O4 y radio hasta T2 que vaya de T2 a T3.
- Sigue trazando un arco con centro en O1 y radio hasta T3 que vaya de T3 a T4.
- Para acabar, dibuja un arco con centro en O3 y radio hasta T4 que vaya de T4 a T1.
Aquí abajo tienes un vídeo con todo el proceso desarrollado paso a paso.
Óvalos conociendo los ejes
Este es el procedimiento más complejo de todos los referentes a óvalos. Para resolverlo te proporcionan los dos ejes del óvalo, representados por los segmentos AB para el eje mayor y CD para el eje menor. Tu punto de partida se parecerá a este:
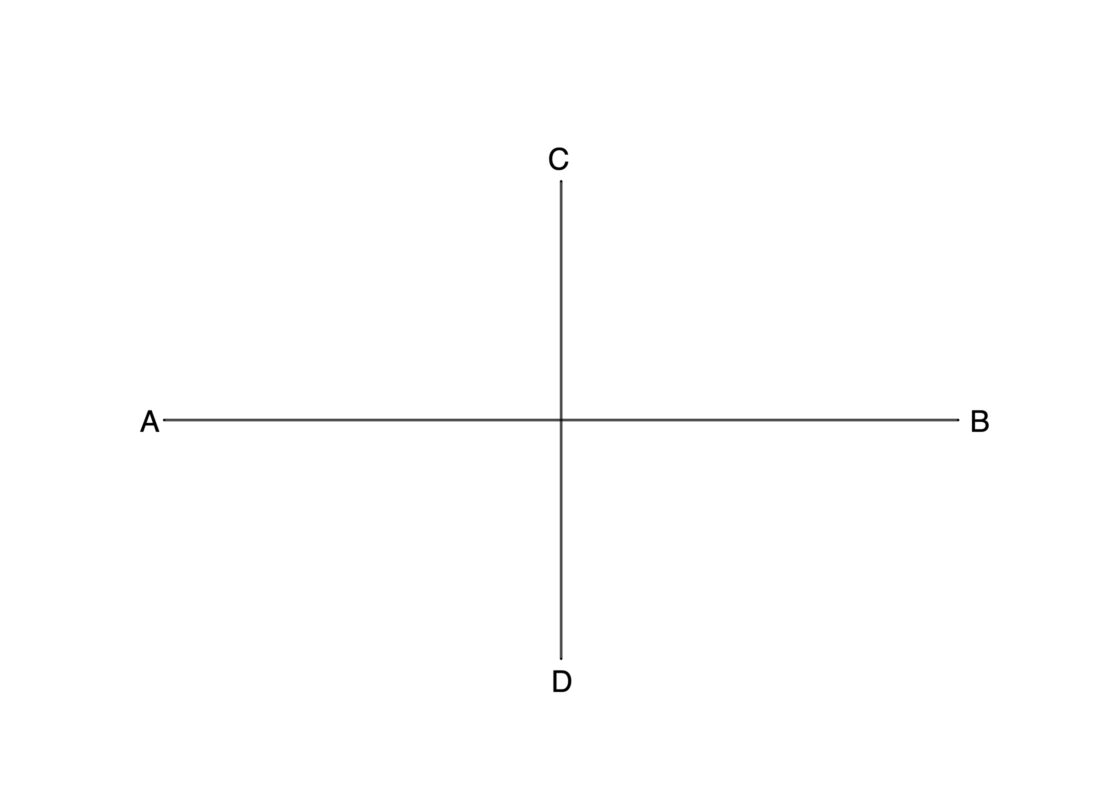
- Prolonga el eje menor CD, ya que sobre esa prolongación tendrás los centros de los arcos inferior y superior.
- Con centro en O (centro del óvalo, donde se cortan los dos ejes) y radio hasta A, dibuja un arco que corta a esa prolongación en el punto E.
- Une los puntos A y C con una línea.
- Con centro en C y radio hasta E dibuja un arco que corta al segmento AC en el punto F.
- Traza la mediatriz del segmento AF. Donde esa mediatriz corta al eje mayor tienes el centro O1, y donde corta a la prolongación del eje menor tienes O2.
- Con centro en O y radio hasta O1 traza un arco que corte al eje mayor en el punto O3.
- Si trazas un arco con centro en O y radio hasta O2, donde ese arco corta a la prolongación del eje menor tienes O4.
- Dibuja circunferencias con centro en O1 y O3 y radio hasta A y B respectivamente.
- Ahora dibuja líneas que pasen por los centros O1, O2, O3 y O4. Donde esas líneas cortan a las circunferencias que dibujaste antes tienes T1, T2, T3 y T4. Los puntos de tangencia donde se cambia de un arco a otro.
- Como en ejercicios anteriores, con centro en O1 y radio hasta T1, dibuja un arco que vaya de T1 a T2.
- Continúa dibujando un arco con centro en O2 y radio hasta T2 que vaya de T2 a T4.
- A continuación traza otro arco con centro en O3 y radio hasta T3 que vaya de T3 a T4.
- Para finalizar, con centro en O4 y radio hasta T1, dibuja un arco que vaya de T1 a T3.
Aquí abajo tienes un vídeo en el que puedes ver como se realiza el proceso completo paso a paso.
Dibujar un óvalo inscrito en un rectángulo
Este ejercicio es una variante del anterior. Para resolverlo todo lo que tienes que hacer es las mediatrices de los lados, dividiendo el rectángulo en cuatro partes iguales. Las líneas que dividen esas partes, son los ejes del óvalo. Una vez sabido esto, solo tienes que solucionarlo utilizando el método que tienes más arriba.
Óvalo conociendo los ejes (Método impreciso)
Este es un método que aparece en el libro de primero de bachillerato del Editorial Paraninfo. A mi personalmente no me gusta nada porque es un método impreciso. Por ese motivo me parece absurdo enseñarlo cuando más arriba tienes un método que si es preciso.
En la siguiente aplicación interactiva puedes mover los puntos A y C para verificar la construcción. Puedes hacer zoom con la rueda del ratón para acercarte. Comprueba que el óvalo resultante no pasa por los puntos que delimitan los ejes.
Óvalo de 8 centros (imperfecto)
Este procedimiento a mi personalmente a mi no me gusta nada. Lo incluyo aquí a título informativo. He creado esta aplicación interactiva para demostrar lo imperfecto que es, el cual es el principal motivo por el que no me gusta y por el que no lo suelo explicar en mis clases cuando explico los otros óvalos. Personalmente creo que es una aberración geométrica sin sentido. Puestos a hacer algo tan atroz, creo que tiene mucho más sentido dibujar una elipse, ya que además parte de la construcción de ésta figura se basa en un procedimiento para dibujar elipses. Puedes mover los puntos azules para ver lo mal que ajustan las curvas y lo poco práctica que es esta técnica.
No obstante, estoy abierto a críticas (constructivas). Si crees que estoy equivocado y que es importante explicar este procedimiento en clase, puedes dejar tu comentario abajo y te aseguro de que estaré encantado de leerlo y discutirlo.
