Giro de rectas en sistema diédrico

Cuando giramos rectas en sistema diédrico lo que debemos hacer es girar dos puntos en el mismo sentido, y el mismo ángulo. En determinadas ocasiones (cuando la recta pasa por el eje de giro) nos bastará con girar un solo punto, ya que uno permanece inalterado.

Girar una recta cuando corta al eje de giro

Para este tipo de ejercicios te proporcionan el eje de giro, representado por una recta perpendicular al plano vertical o al horizontal. También conoces una recta que es la que hay que girar, y por último un valor en grados que corresponde al radio de giro. Tu punto de partida será algo similar a éste. Se pide girar la recta 90 grados en sentido de las agujas del reloj.

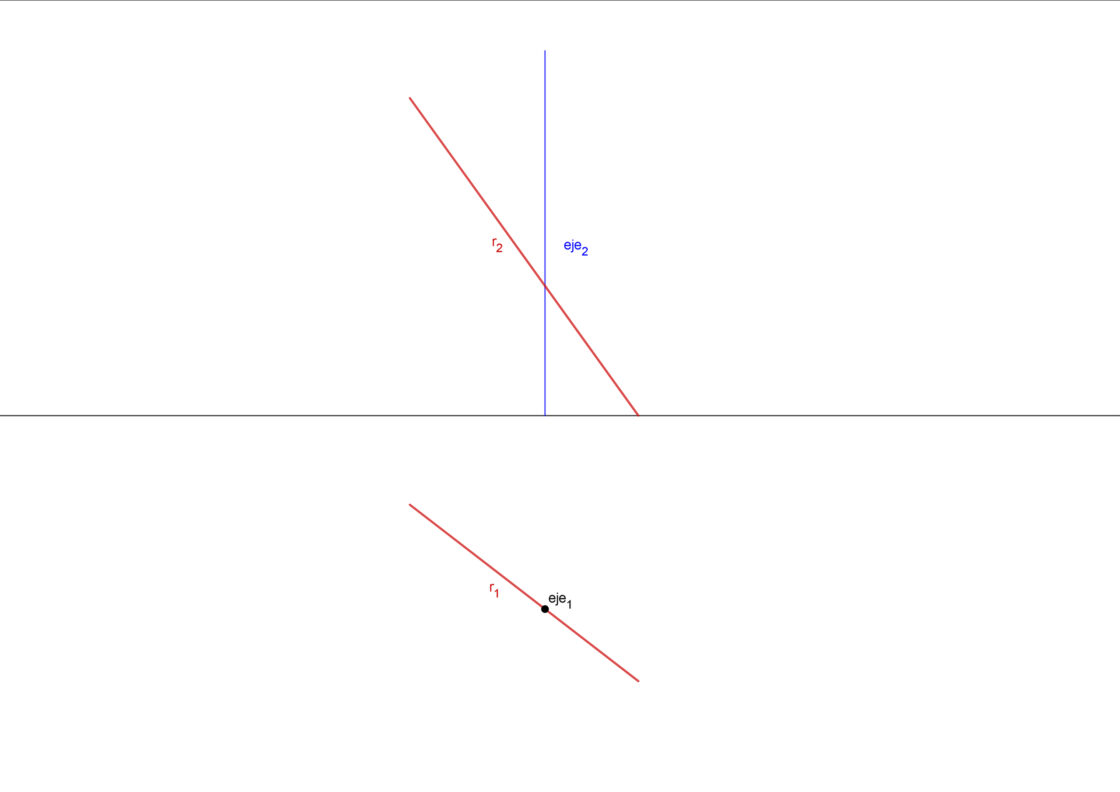
Date cuenta de que al girar un punto alrededor del eje su altura no cambiará. Por lo tanto ese punto se moverá de forma paralela a la línea de tierra sobre la proyección en el plano vertical. En el plano horizontal, en cambio, se moverá de forma circular alrededor del eje de giro, que en el plano horizontal se representa como un único punto en éste caso. Date cuenta de que este caso es el más sencillo. Para dibujar una recta necesitas dos puntos, y uno de ellos (el de intersección con el eje de giro) permanece inalterado. Por ese motivo solo necesitas mover otro punto.

Puedes elegir cualquier punto para girarlo y luego unirlo con el punto de intersección. No obstante, yo te recomiendo utilizar la traza del plano sobre el plano horizontal. De esa manera te resultará más sencillo.

1. Empieza por marcar el punto de intersección de la recta con el eje en la proyección vertical. A ese punto puedes llamarlo I₂. Date cuenta de que la proyección horizontal del punto de intersección va a coincidir con la proyección horizontal del eje de giro.
2. Puedes llamar H₁ a la traza horizontal de la recta. Con centro en la proyección horizontal del eje, y radio hasta H₁, realiza un arco de 90 grados para determinar la nueva posición de H₁, a la que puedes llamar H₁‘
3. Levanta una perpendicular a la línea de tierra que pase por H₁‘ para hallar la nueva posición de H₂, a la que llamaremos H₂‘
4. Ahora dibuja una recta que pase por H2′ e I2 por un lado, y otra que pase por H1′ y eje1 por otra. Esas dos rectas determinan la nueva posición de la recta tras el giro.

Giro de rectas que no cortan al eje de giro

Este caso es mucho más común cuando giras varias rectas al mismo tiempo, de manera que una de ellas puede pasar por el eje, pero las demás ya no lo hacen. Llegados a este punto es interesante recordar como girar elementos en geometría, que ya vimos en primero de bachillerato. El procedimiento es similar al anterior, salvo que en este caso si que debes girar dos puntos de manera obligatoria. Como en el caso anterior, uno de ellos puede ser la traza horizontal, lo que te facilitará las cosas. Tu punto de partida debe parecerse algo a ésto.

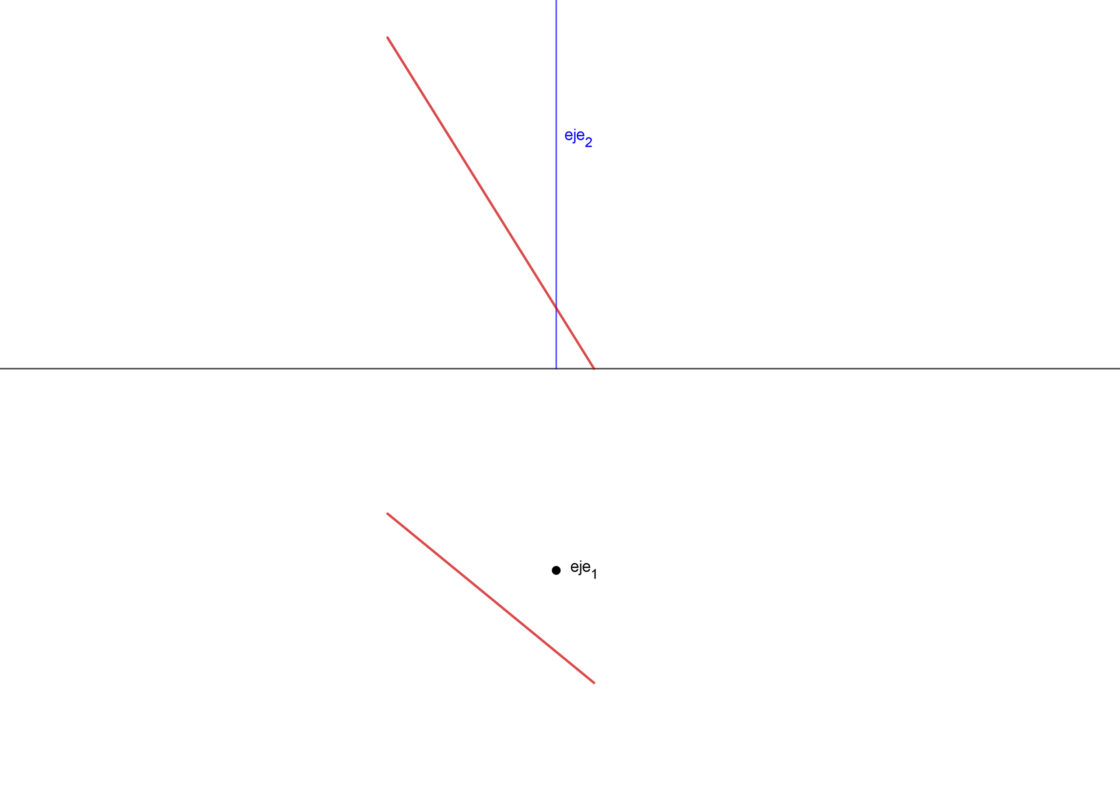
Por hacerlo distinto, en este caso vamos a girarlo 90 grados pero en sentido contrario a las agujas del reloj. Para mayor comodidad, puedes considerar que la recta es un segmento definido por dos puntos. Si no te proporcionan esos puntos, los puedes delimitar tu. En este caso, al punto superior lo llamaremos A y al punto inferior, que corresponde con la traza horizontal lo llamaremos H. Así pues tienes A₁ y A₂ para el punto A y H₁ y H₂ para el punto H.

1. Empieza girando el punto A₁ alrededor del eje de giro los 90 grados en sentido contrario a las agujas del reloj que te están solicitando. De ese modo obtienes la nueva posición del punto, que es A₁‘.
2. La proyección vertical del punto A se mueve paralela a la línea de tierra, porque conserva su altura. Por lo tanto dibuja una paralela a la línea de tierra que pase por A₂ y una perpendicular que pase por A₁‘. Donde esas dos líneas se cruzan tienes A₂‘.
3. Ahora toca girar H₁ 90 grados alrededor del eje. En este proceso obtienes H1′, que es la nueva posición de la traza horizontal de la recta después de haber girado.
4. Levanta una perpendicular a la línea de tierra que pase por H₁‘, donde corta a la línea de tierra tienes H₂‘, que es la nueva proyección vertical de la traza horizontal después de haber girado.
5. Para terminar, une A₂‘ con H₂‘ por un lado para marcar la nueva proyección vertical de la recta después del giro. Por otro lado, une A₁‘ con H₁‘ para obtener la nueva proyección horizontal de la recta después de haber girado.

Girar una recta hasta transformarla en frontal

Recuerda que una recta frontal es paralela al plano vertical. Por este motivo la proyección horizontal de cualquier recta frontal será siempre paralela a la línea de tierra. Así pues, debes girar una recta el ángulo necesario para que su proyección horizontal acabe quedando paralela a la línea de tierra. Este es un método muy útil para saber cuanto mide esa recta en realidad. Tu punto de partida es éste.

1. Empieza por marcar un eje de giro. Para que sea más fácil, haz que pase por un punto de la recta. Ese punto de intersección llámalo A. Date cuenta de que la proyección horizontal de ese punto va a coincidir con la proyección horizontal del eje.
2. Como la nueva posición de la recta será paralela al plano vertical, dibuja una línea paralela a la línea de tierra que pase por A₁. Luego, con centro en A₁, dibuja arcos con radio hasta V₁ y H₁ hasta cortar a esa paralela. Esos puntos serán la nueva posición de las proyecciones horizontales de las trazas al girar. Puedes llamarlos V₁‘ y H₁‘.
3. Para continuar, dibuja una línea paralela a la línea de tierra que pase por V₂. Esto es así porque al girar la altura de los puntos no va a variar. Ahora traza perpendiculares a la línea de tierra que pasen por V₁‘ y H₁‘. Donde la perpendicular que pasa por V₁‘ corta a esa paralela tienes V₂‘, que es la nueva posición de la traza vertical de la recta. Donde la perpendicular que pasa por H₁‘ corta a la línea de tierra tienes H₂‘, que es la nueva posición de la proyección vertical de la traza horizontal de la recta.

Girar una recta hasta transformarla en horizontal

Vamos a partir de la misma recta del supuesto anterior. Pero en este caso lo que se pretende es transformarla en horizontal. Es decir, girarla lo suficiente como para que acabe estando paralela al plano horizontal. De esa manera, la nueva proyección de la recta sobre el plano horizontal será su verdadera magnitud. Así pues, el punto de partida será el siguiente.

Date cuenta de que en este caso, el eje de giro será una recta de punta. Es decir, una recta perpendicular al plano vertical. Para mayor comodidad, haremos que atraviese la propia recta.

1. Empieza por definir el eje de giro. Como te decía antes, para que sea más fácil, marca un punto sobre la recta. Ese punto, al que puedes llamar A, será el punto de intersección del eje de giro con la recta. Date cuenta que la proyección vertical del punto (que es A₂) coincide con la proyección vertical del eje de giro, representado por eje₂
2. Dibuja una paralela a la línea de tierra que pase por A₂. Y luego, con centro en A₂ y radio hasta V₂ y H₂, traza dos arcos para determinar sobre esa paralela los puntos V₂‘ y H₂‘. Estos puntos serán la nueva posición que ocupen las proyecciones verticales de las trazas al girar hasta ponerse horizontales.
3. Las proyecciones horizontales de las trazas se desplazan de forma paralela a la línea de tierra, ya que no varía su alejamiento. Así pues, traza una perpendicular a la línea de tierra que pase por V₂‘ para determinar sobre ella V₁‘, que es la nueva posición de la proyección horizontal de la traza vertical de la recta.
4. Ahora dibuja una perpendicular a la línea de tierra que pase por H₂‘, y una paralela a la línea de tierra que pase por H₁. Donde esas dos rectas se cortan tienes el punto H₁‘, que es la nueva posición de la proyección horizontal de la traza horizontal de la recta después de haber girado.

Girar una recta frontal hasta convertirla en paralela a la línea de tierra

En este caso debes marcar un eje de giro perpendicular al plano vertical. Para que sea más fácil, haz que corte con la recta que pretendes girar. En este ejemplo el punto A determina la intersección de la recta frontal con el eje de giro. Cómo puedes ver, la proyección vertical del punto A coincide con la proyección vertical de la recta.

1. Cómo quieres transformar la recta frontal en paralela a la línea de tierra, debes dejarla paralela a la misma. Por tanto, empieza por trazar una recta paralela a la línea de tierra que pase por el punto A₂.
2. Ahora, con centro en A₂ y radio hasta H₂, dibuja un arco hasta cortar a la paralela que dibujaste en el paso anterior. Ese punto de intersección será H₂‘, la nueva posición de H₂ después de girar.
3. A continuación dibuja una paralela a la línea de tierra que pase por A₁, y una perpendicular a la línea de tierra que pase por H₂‘. El punto donde se cortan es H₁‘, la nueva posición de la traza horizontal de la recta después de girar.

Girar una recta horizontal hasta convertirla en paralela a la línea de tierra

Parar girar una recta frontal hasta transformarla en paralela a la línea de tierra debes marcar el eje de giro perpendicular al plano horizontal. Como siempre, para mayor comodidad, haz que el eje de giro corte a la recta en un punto cualquiera A de ella. En éste caso, la proyección horizontal del punto de intersección va a coincidir con la proyección horizontal del eje de giro.

1. Empieza por trazar una paralela a la línea de tierra que pase por A₁, ya que ahí estará la nueva posición de la recta después de girar.
2. Con centro en A₁ y radio hasta V₁ traza un arco hasta cortar a la paralela que dibujaste en el primer paso. El punto de intersección será V₁‘, la nueva posición de la proyección horizontal de la traza vertical de la recta.
3. Ahora traza una paralela a la línea de tierra que pase por A₂, y una perpendicular a la línea de tierra que pase por V₁‘. Donde esas dos líneas se cortan tienes el punto V₂‘, la nueva posición de la traza vertical de la proyección vertical de la recta.