Una epicicloide pertenece al grupo de las curvas cíclicas. En dibujo técnico, es la curva que realiza un punto P que se encuentra en una circunferencia, al desplazarse sobre la parte exterior de otra circunferencia, que hace de base fija. A la circunferencia que gira se le denomina ruleta. Aquí abajo tienes una epicicloide interactiva. Moviendo la barra del movimiento verás como evolucionan los distintos puntos al moverse. Si modificas el radio podrás ver como es la epicicloide alargada, normal y la acortada.
Por explicarlo de otra manera, imagina que dibujaras una cicloide y que luego la base la doblas para que se ajuste a una circunferencia. La curva resultante sería una epicicloide. Sabiendo ésto, ya te puedes imaginar que la construcción es muy similar a la de la cicloide.
Trazar una epicicloide en dibujo técnico
Llegados a éste punto, lo primero que tienes que descubrir es la longitud tanto de la circunferencia ruleta, como de la base. De lo contrario es imposible dibujar correctamente la epicicloide. Para ello debes rectificar un arco de la ruleta, y luego hacer el proceso inverso para ver a que cantidad corresponde en la circunferencia que hace de base.
Si no recuerdas como se hace, te dejo aquí una pequeña imagen para que te sirva de chuleta. Y si no, puedes visitar la entrada donde explico como rectificar un arco menor de 90 grados.
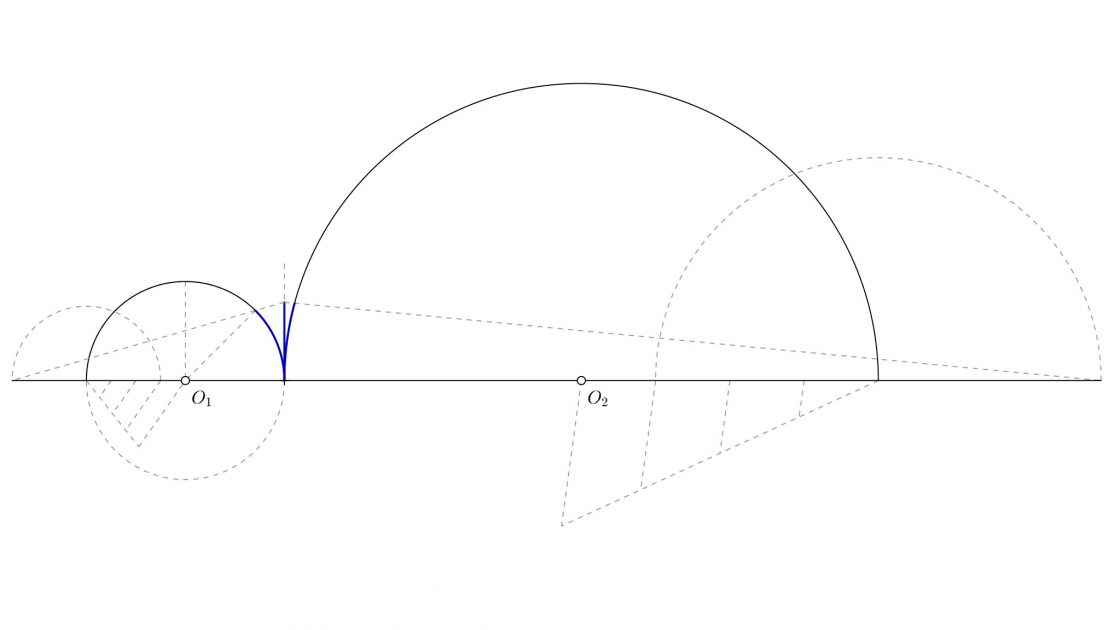
Hallar el recorrido de la ruleta
La circunferencia que rueda por la parte exterior se denomina ruleta. Lo primero que necesitas saber es hasta donde llega con una vuelta completa. Para eso necesitas realizar la rectificación. En ésta ocasión considero mas importante que aprendas a realizar la epicicloide que la propia rectificación. Por ese motivo te propongo un ejercicio ideal para un A3 y que te facilitará la tarea. En el siguiente ejercicio la ruleta mide 4 centímetros de radio, y la circunferencia sobre la que rueda tiene 12 centímetros de radio. De esa manera sabemos que el recorrido de la ruleta será exactamente un tercio de la circunferencia mayor.
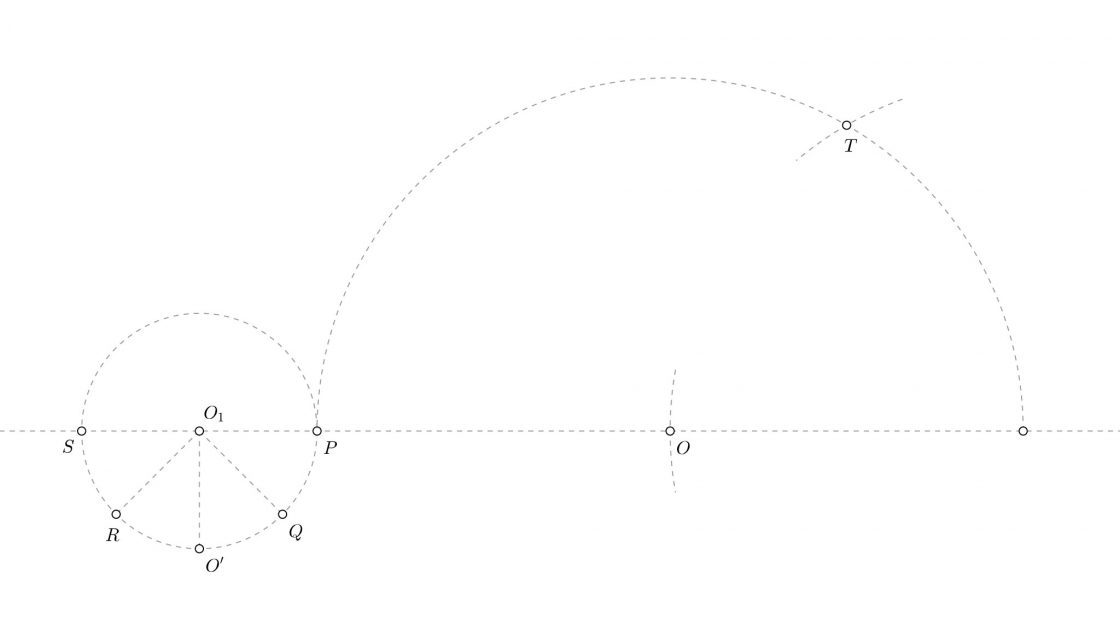
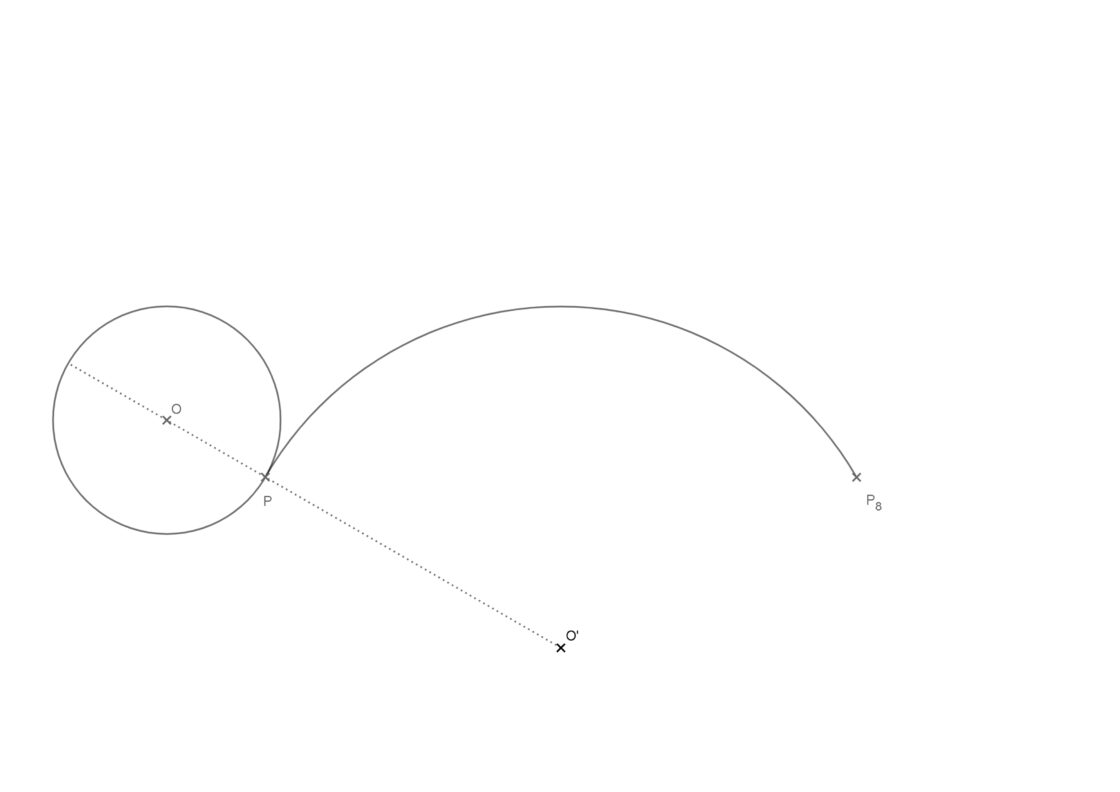
Puede que no puedas realizar el ejercicio con las medidas que propongo porque no tengas hojas DIN A3. También puede pasar que tengas hojas, pero tu compás no te permita hacer arcos de 20cm, o que no tengas alargador de compás. Por ese motivo te ofrezco una alternativa asequible en DIN A4. Puedes pulsar sobre la imagen de aquí abajo para ponerla a pantalla completa y luego imprimirla. Si no, te recomiendo usar un radio de 3cm para la ruleta, y de 9cm para la circunferencia sobre la que gira. De ese modo no tendrás problema. El arco entre P y P8 corresponde al arco que recorre la ruleta en una vuelta completa. De ese modo te evitas tener que hacer la rectificación.
Puntos importantes en la epicicloide
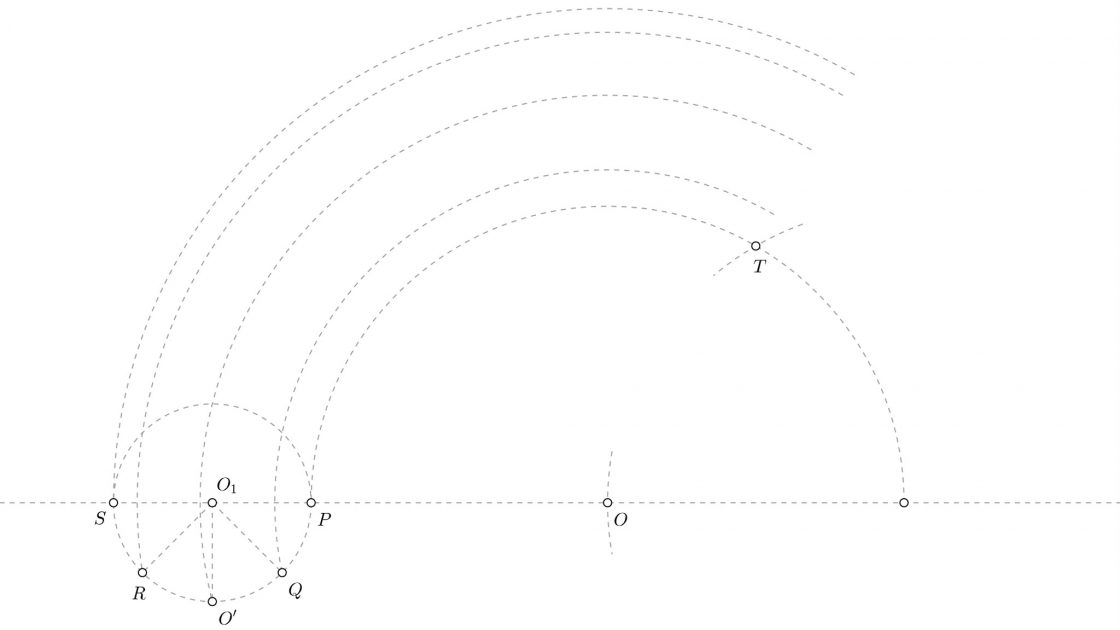
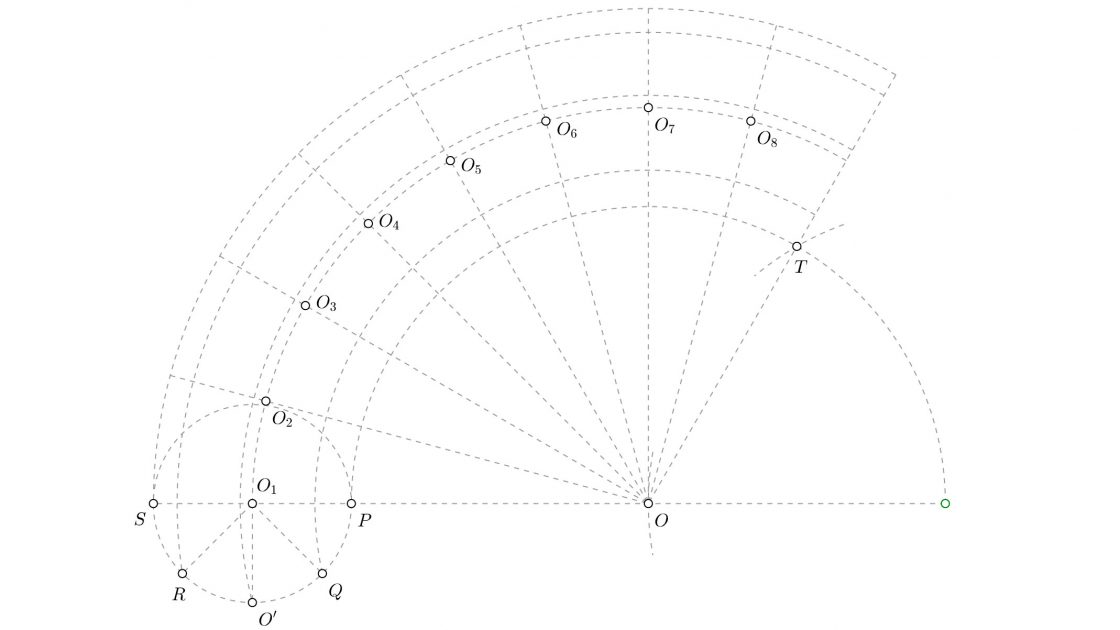
En la imagen superior te he marcado los primeros puntos que debes hallar para poder dibujar la epicicloide. Te voy a explicar como hallarlos uno por uno.
Para hallar el punto T tienes que dibujar un arco con el radio de la circunferencia mayor, con centro en donde te corta el eje que une las circunferencias a la circunferencia mayor. El arco que va de P a T es justo un tercio de la circunferencia, coincidiendo con la longitud de la circunferencia de radio menor.
- Si trazas una perpendicular a la recta que une O1 y O que pase por O1, tendrás el punto O’ en donde corta a la ruleta.
- Ahora dibuja las bisectrices de los ángulos que forman O’ O1 y P por un lado, y O’ O1 y S por el otro. De esa manera hallarás Q y R
- Con centro en O, dibuja arcos que pasen por Q, O’, R y S
Temporización de la epicicloide
El siguiente paso consiste en saber donde está exactamente la ruleta en cada momento. Lo más habitual es dividir el recorrido en ocho partes. Este número es fácil porque es la mitad, y luego la mitad, y de nuevo la mitad. No obstante, si quieres hacer un trabajo más preciso podrías dividirlo en 16 partes. En cualquier caso, cuatro partes no son suficienten para dibujar la epicicloide.
- Sabiendo ésto, tienes que hacer la bisectriz del ángulo que forman P con O y T
- Cada una de esas mitades la debes dividir de nuevo en dos, mediante bisectrices, teniendo ahora cuatro partes.
- Para terminar, divide de nuevo cada una de esas partes usando bisectrices en dos. Así tendrás las ocho partes iguales.
- Dibuja un arco con centro en O y radio hasta O1. Donde este arco corta a las bisectrices tendrás los centros O2, O3, O4…
Como hallar los últimos puntos
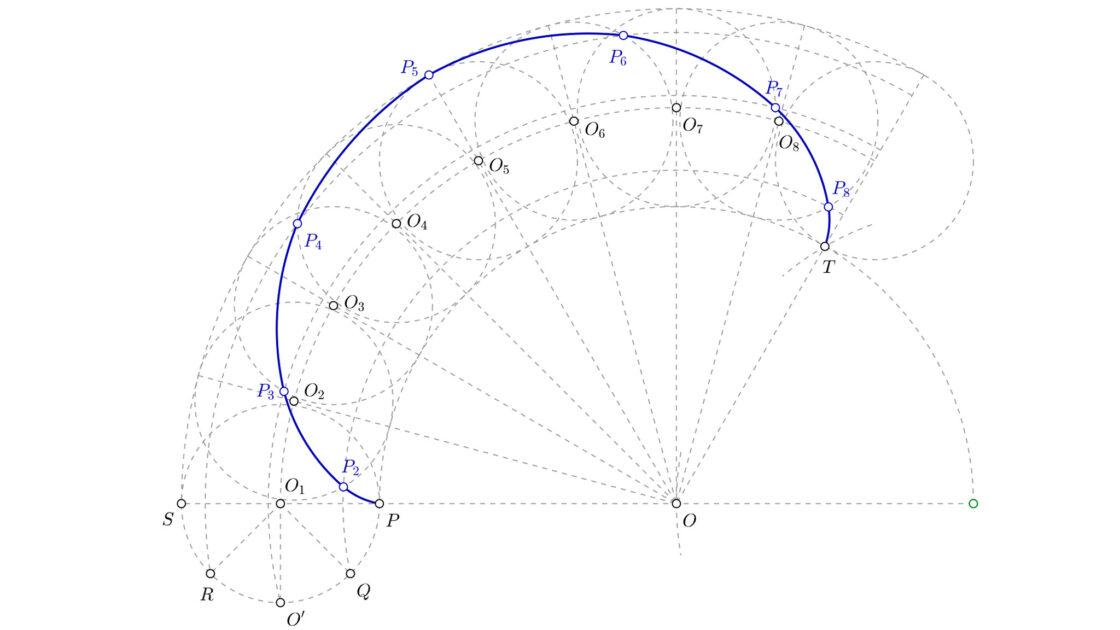
Para terminar la epicicloide tienes que hallar los puntos donde el punto P se encontrará con respecto a cada uno de los centros.
- Con centro en O2 y el radio de la ruleta (recuerda que era 4cm) traza un arco, que cortará a al arco de centro O y radio hasta Q. Ese punto será P2
- Con centro en O3 y el radio de la ruleta, dibuja un arco que cortará al arco de centro O y radio hasta O’. El punto de corte es P3
- Con centro en O4 y radio el de la ruleta, traza un arco que cortará al arco de centro O y radio hasta R. El punto de intersección será P4
- Si prolongas la línea que une O con O5, en el corte con el arco de centro O y radio hasta S tienes el punto P5
- Con centro en O6 y radio igual al de la ruleta, traza el arco que cortará al arco de centro O y radio hasta R. Ese punto de corte es P6
- Con centro en O7 y radio el de la ruleta, dibuja un arco que cortará al arco de centro O y radio hasta O’. En el punto de intersección tienes P7
- Dibuja un arco de centro O8 y radio como el de la ruleta. Ese arco cortará al arco de centro O y radio hasta Q en el punto P8
- Si unes todos esos puntos con una plantilla de curvas tendrás la epicicloie terminada.
Aquí abajo tienes una aplicación interactiva para entender la construcción que acabas de realizar. El punto T se puede mover, y de esa manera ves como gira la ruleta. El punto P se mueve dibujando la curva de la epicicloide.
Epicicloide acortada
¿Y que pasa cuando el punto no se encuentra en la propia circunferencia, sino dentro de la ruleta? En éste caso estamos hablando de una epicicloide acortada. Para poder dibujarla es imprescindible dibujar primer la epicicloide normal, por lo que nuestro punto de partida será el anterior, pero con el punto X, que será el punto que se desplaza, dentro de la ruleta. No dibujes la curva de la epicicloide normal, ya que eso no lo necesitas.
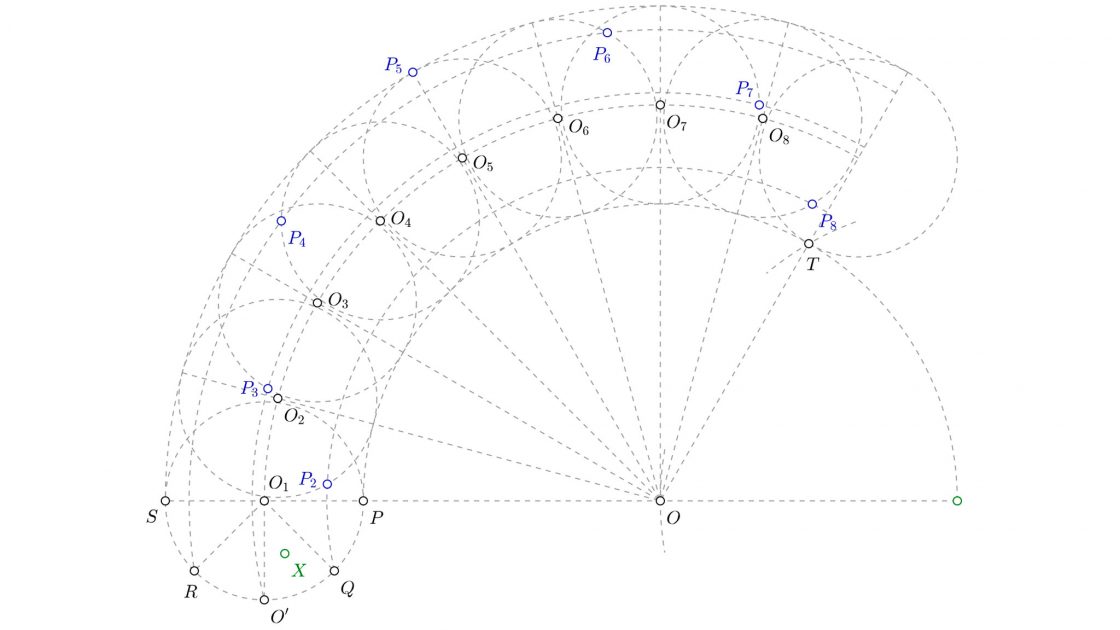
- Lo primero que tienes que conocer es exactamente la distancia que hay entre O1 y X (en caso de que no la conozcas). Para ello, traza un arco con centro en O1 y radio hasta X. Éste arco cortará en el punto X1.
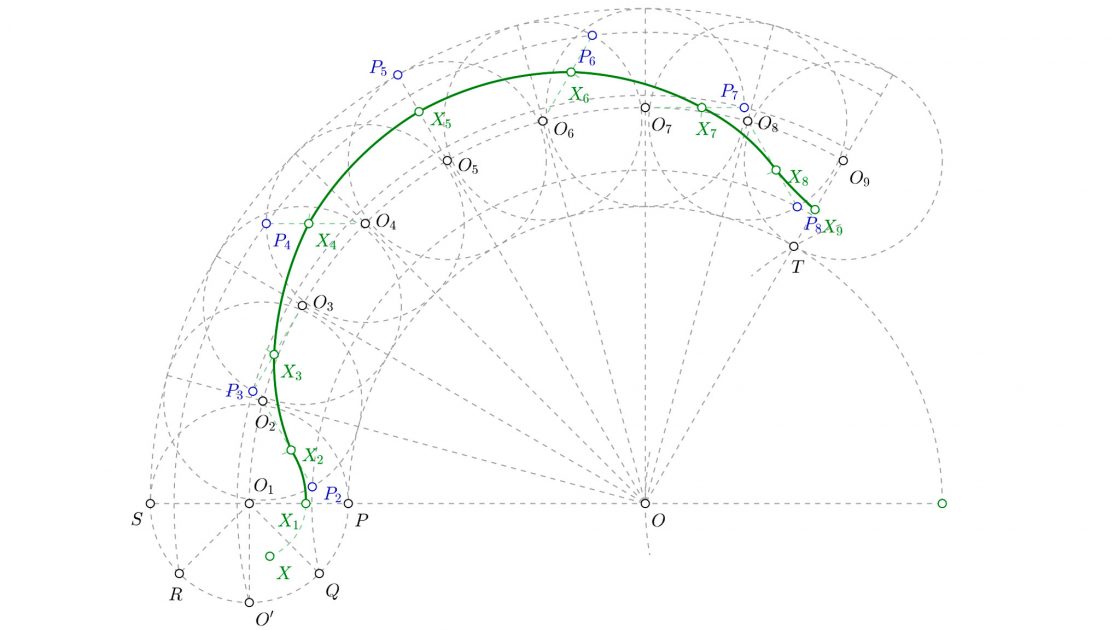
- Traza la línea que une O2 con P2, y sobre ella mide la distancia de O1 a X1. De esa manera tienes la posición del punto X2.
- Une O3 con P3, y sobre esa recta lleva la medida de O1 a X1, de esa manera encuentras X3.
- Repite el mismo proceso con los demás centros y puntos para hallar X4, X5, X6, X7, X8 y X9
- Une los puntos X1, X2, X3… con una plantilla de curvas y ya tienes tu epicicloide acortada terminada.
Epicicloide alargada
En el caso de la epicicloide alargada, el punto se encuentra fuera de la ruleta. Al igual que en el caso anterior, es necesario hallar los puntos de la epicicloide normal para poder resolverlo. El método de resolución es muy parecido al del caso anterior, pero en ésta ocasión será necesario prolongar el radio para hallar los puntos. Voy a explicártelo mejor paso a paso. Tu punto de partida será éste:
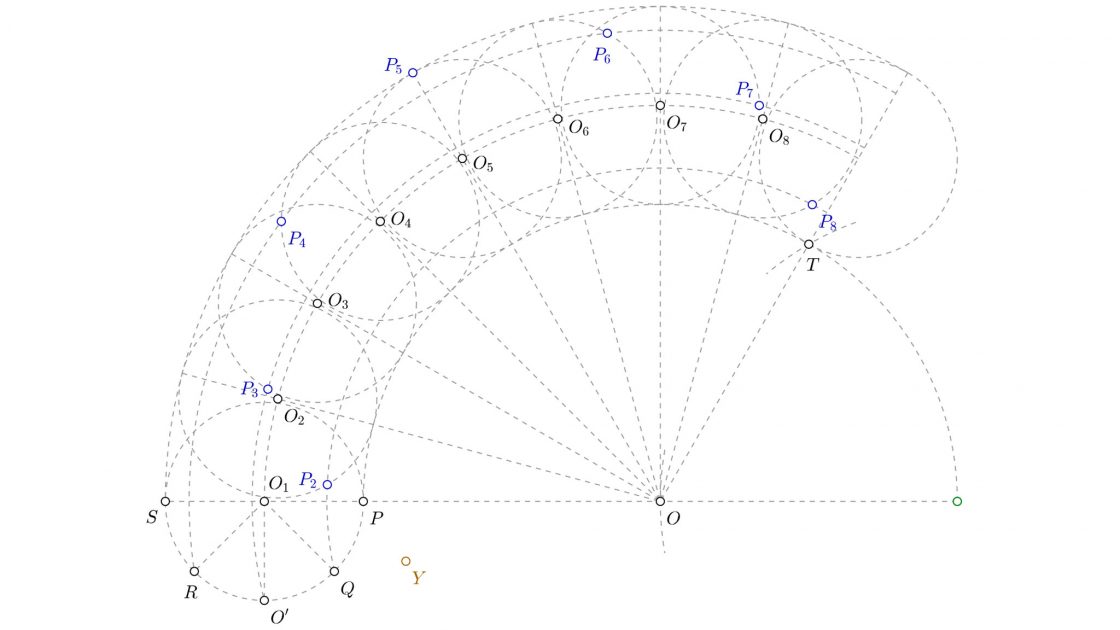
- Con centro en O1 traza un arco que tenga radio hasta Y para ver donde corta al segmento OP. Ese punto de corte será Y1, el primer punto de la epicicloide alargada.
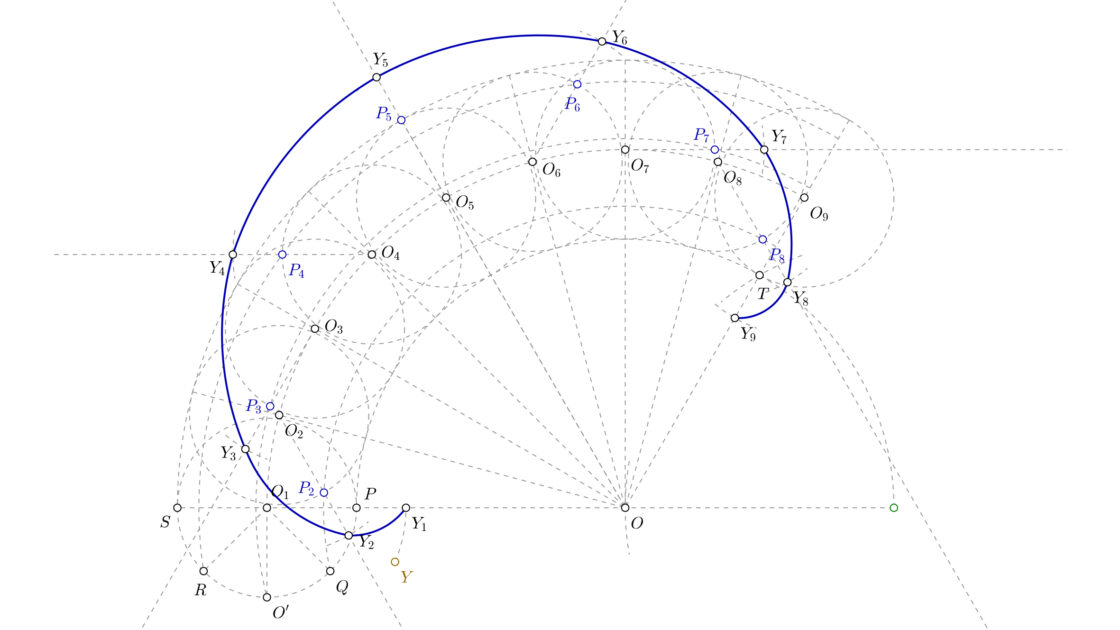
- A continuación, con centro en O2 y radio O1Y dibuja un arco que cortará a la prolongación del segmento O2P2 en un punto que será Y2.
- Repite este proceso con todos los demás puntos. Con centro en O3 y radio O1Y dibuja un arco que corta a la prolongación del segmento O3P3 en el punto Y3
- Así, sucesivamente, halla los demás puntos Y4, Y5, Y6, Y7, Y8 e Y9. Uniendo todos estos puntos con la plantilla de curvas tendrás la epicicloide alargada.
Ayúdame a mejorar esta entrada
¿Hay algo que no entiendes? ¿Has descubierto una errata? Si es así, dime cuál y lo corregiré. ¿Crees que falta información o que hay algo que se podría mejorar? ¿Tienes un problema sin solución?
Al plantear tu duda ayudas a todas las personas que tienen la misma duda que tú, y me ayudas a enriquecer este artículo para hacerlo más útil para todos. Tus aportaciones ayudarán a todo el que lea este artículo después de ti.
«Un voto inferior a 5 sin una explicación es un reflejo de tu propia inteligencia.» -Proverbio chino.
