Una cicloide en dibujo técnico es la trayectoria que realiza un punto de una circunferencia que rueda sobre una recta sin realizar deslizamiento. A la recta se le llama directriz y a la circunferencia se le suele dar el nombre de ruleta o generatriz. En otro apartado veremos como resolver las epicicloides o hipocicloides, cuando son dos circunferencias tangentes las que originan la cicloide.
Cicloide normal
Es el caso más común, cuando el punto generador de la cicloide se encuentra en el perímetro de la circunferencia generatriz. Veamos como se realiza
Desarrollo
- Dados un punto P en la circunferencia de la ruleta de centro O1
- Rectificamos la circunferencia de centro O1 (incluyo la imagen por si no recordáis el proceso).
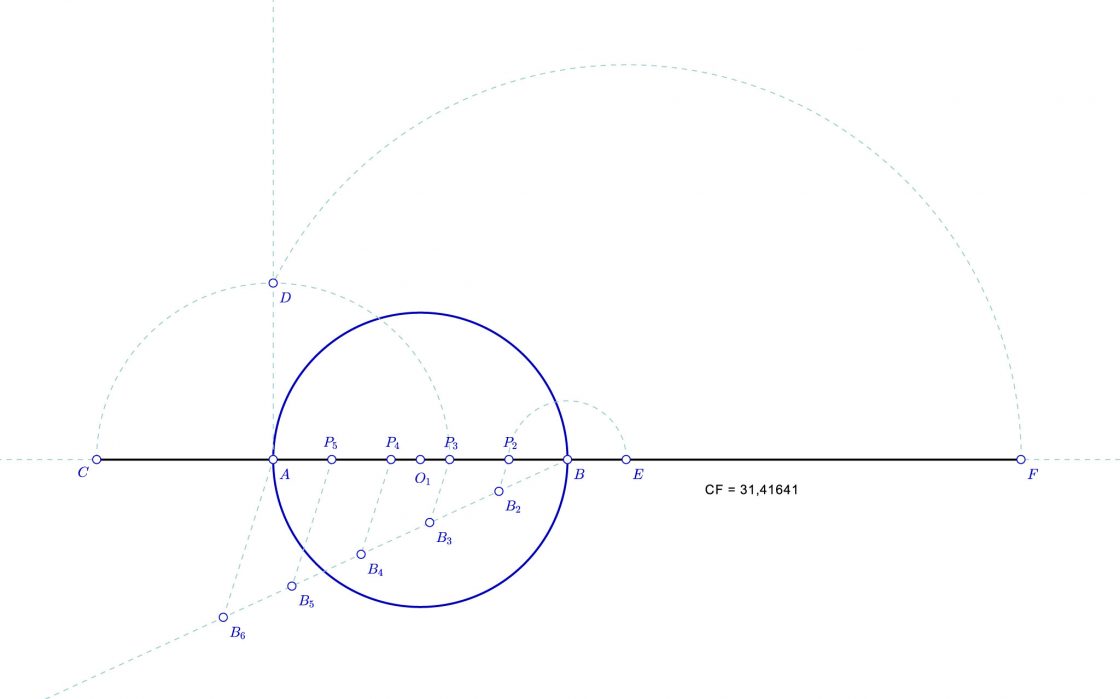
En caso de que fuera necesario, podríamos trasladar la rectificación una vez conocida su longitud. En la siguiente imagen he eliminado los pasos intermedios y desplazado la rectificación para mayor comodidad.
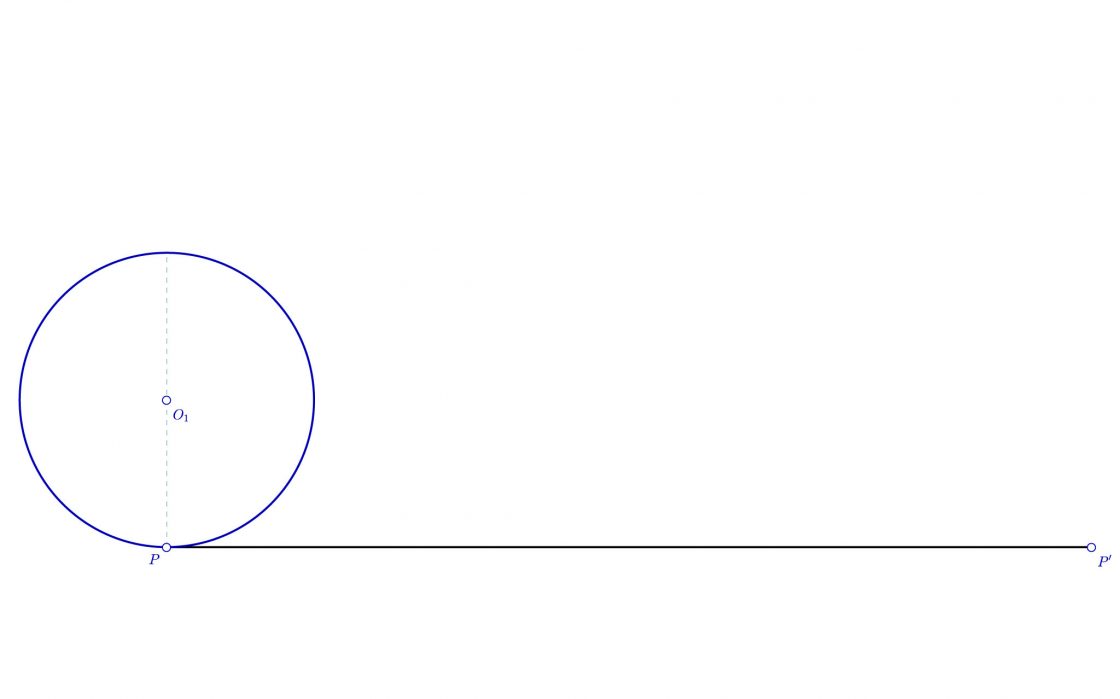
- Dividimos la circunferencia generatriz en ocho fracciones utilizando bisectrices de los ejes.
- Ahora dividiremos el desarrollo de la circunferencia en ocho partes iguales usando el teorema de Tales.
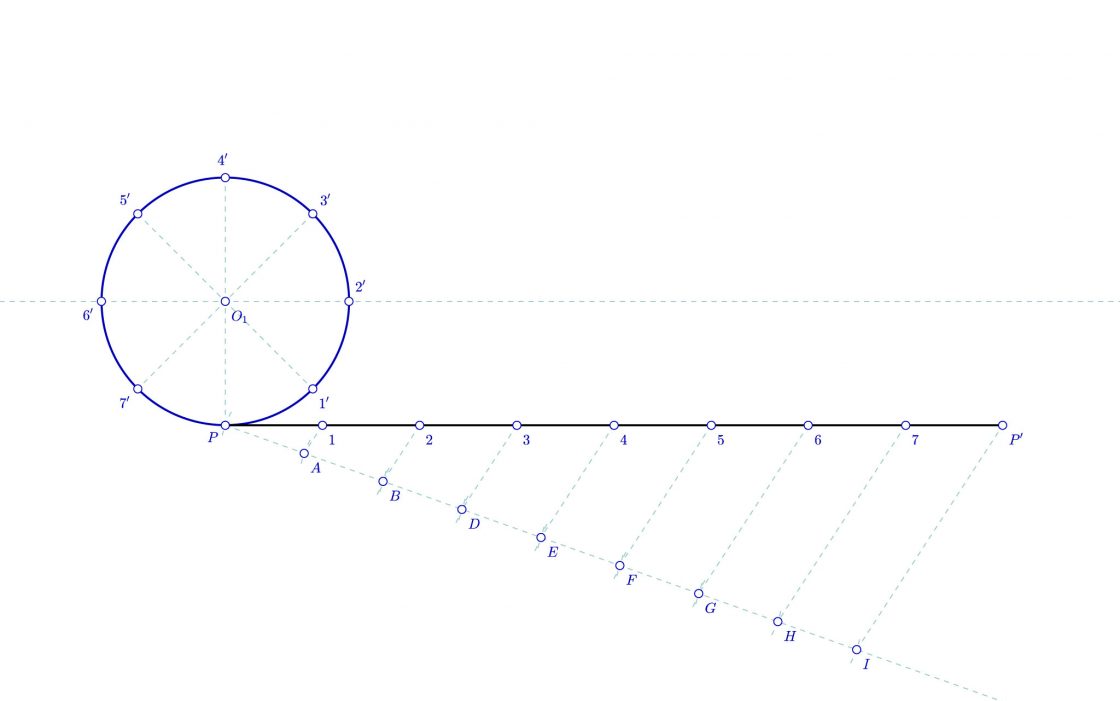
Conclusión
Como podéis observar, he llamado a los puntos de la circunferencia en el orden de corte, y a los puntos sobre la directriz también, de tal manera que al girar, 1 coincidirá con 1′, el punto 2 coincidirá con el punto 2′ y así sucesivamente. Creo que así se puede visualizar esta construcción de forma más sencilla.
- Trazamos una perpendicular a la directriz que pasa por cada punto que hemos marcado. De ese modo hallamos O2, O3, O4… que son los puntos en los que se encuentra el centro de la circunferencia al pasar sobre cada punto en cuestión.
- Realizamos paralelas a la directriz que pasen por los puntos de la circunferencia que marcan sus secciones, es decir, una que pase por 1′ y 7′ y otra que pasa por 3′ y 5′
- Dibujamos circunferencias del mismo radio que O1 con centro en cada uno de los puntos que hemos hallado antes O2, O3, O4…
- Donde cada una de esas circunferencias corta a las paralelas a la directriz en el segmento que les corresponde tenemos puntos que pertenecen a la cicloide. Por ejemplo, donde la circunferencia de centro O2 corta a la paralela que pasa por 1′ tenemos el primer punto. A éstos puntos los llamaremos J, K, L…
- Si trazamos la curva que pasa por estos puntos, tendremos la cicloide buscada.

Aquí abajo tienes una aplicación interactiva que espero que te ayude a comprender como se genera esta curva. Puedes mover el punto T para ver como se comporta el punto P y porqué esta curva tiene esta apariencia y porqué se dibuja cada una de las lineas del proceso.
Cicloide acortada o reducida
La cicloide acortada o reducida se genera cuando el punto generador se encuentra en un punto interno de la ruleta o generatriz y que gira con ella al trazar su movimiento.
En dibujo técnico la forma de dibujar ésta cicloide es similar a la anterior. Más aún, para hallarla primero debemos dibujar la cicloide normal. Así pues, vamos a continuar desde éste punto.
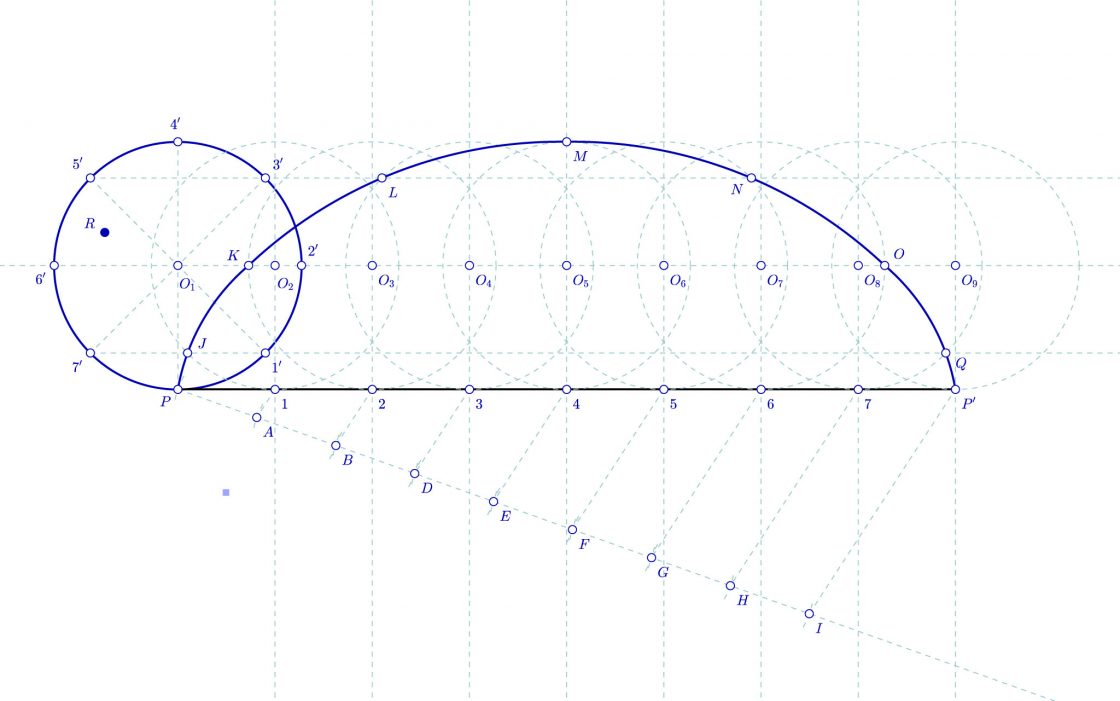
Desarrollo
En primer lugar debemos trasladar el punto generador R sobre la perpendicular a la recta directriz, hallando el punto R’ a partir del cual comenzaremos a trabajar. Si se nos solicitara hallar la forma geométrica con inicio en el punto R, solo tendríamos que desplazarla una ver dibujada.
Ahora sobre cada uno de los segmentos que unen O1 con J, O2 con K, O3 con L, y así sucesivamente, trazamos un arco con la distancia que separa O1 del punto generador R. En el punto en el que corta obtenemos los puntos J’, K’, L’ que unidos darán lugar a la cicloide acortada que buscamos.
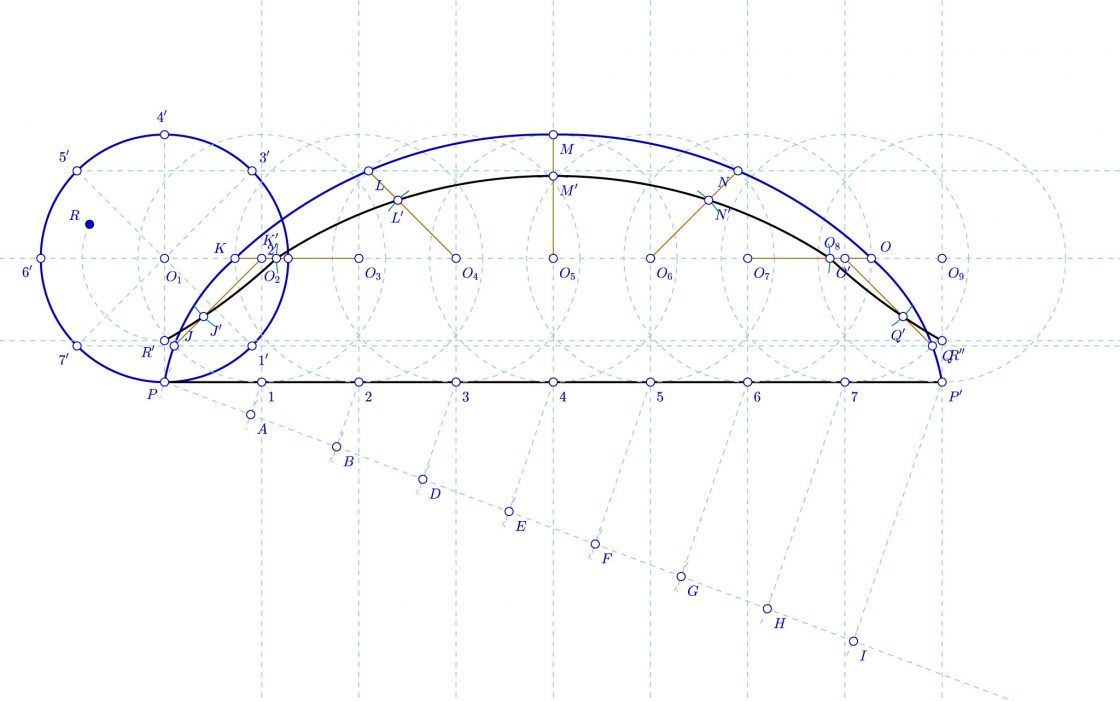
Daos cuenta de que cuanto más cerca se encuentre el punto generador de la circunferencia exterior, más se parecerá su recorrido al de la cicloide normal, y cuanto más se acerce al centro de la circunferencia, más parecerá una recta.
Cicloide alargada
En una cicloide alargada, el punto generador se encuentra fuera de la circunferencia, rotando de forma sincronizada con ésta. Al igual que en el caso anterior, realizaremos el trazado normal antes de proceder a su resolución completa.
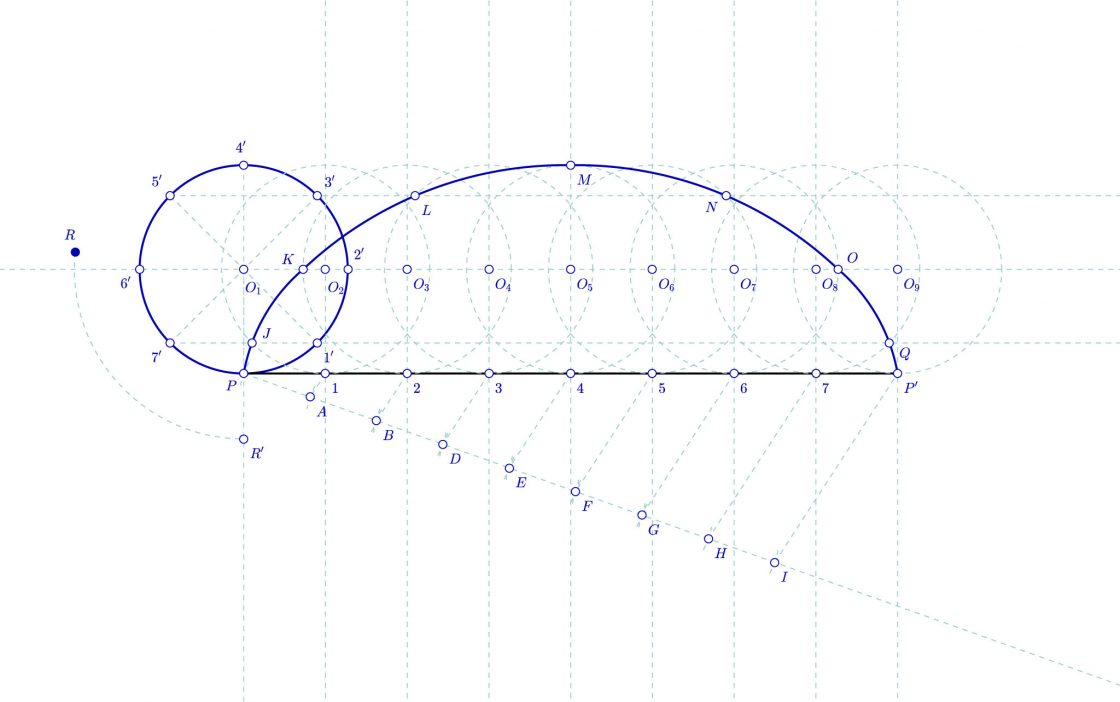
Resolución
Tal como pasaba con el ejercicio anterior, debemos trasladar el punto R para hallar el punto R’ sobre la prolongación del radio de la circunferencia.
El procedimiento es muy parecido al anterior, la diferencia radica en que los puntos J’, K’, L’… Los hallamos sobre el punto de corte de la prolongación del segmento que une O2 con J, O3 con K, y así sucesivamente. La resolución por tanto sería la siguiente.
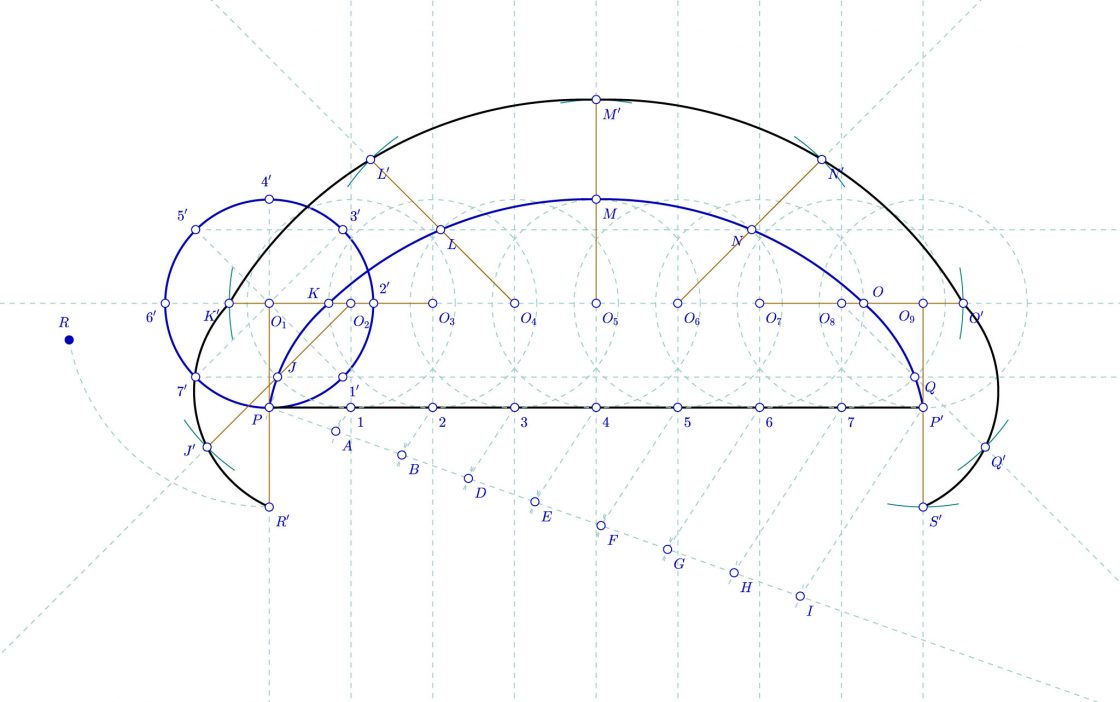
Tangentes a la cicloide
Las rectas tangentes a la cicloide se hallan como las tangentes a cualquier otro tipo de curva cíclica. Da lo mismo si se trata de una cicloide alargada, acortada o normal. En la aplicación de aquí abajo puedes mover el deslizador para ver como se comporta la recta tangente.
Para poder hallar la tangente necesitas conocer el radio de la ruleta, y tener la curva de la cicloide. Tu punto de partida debería ser algo semejante a la imagen siguiente. Puedes pulsar sobre ella para verla a pantalla completa e imprimirla en un DIN A4 para practicar.
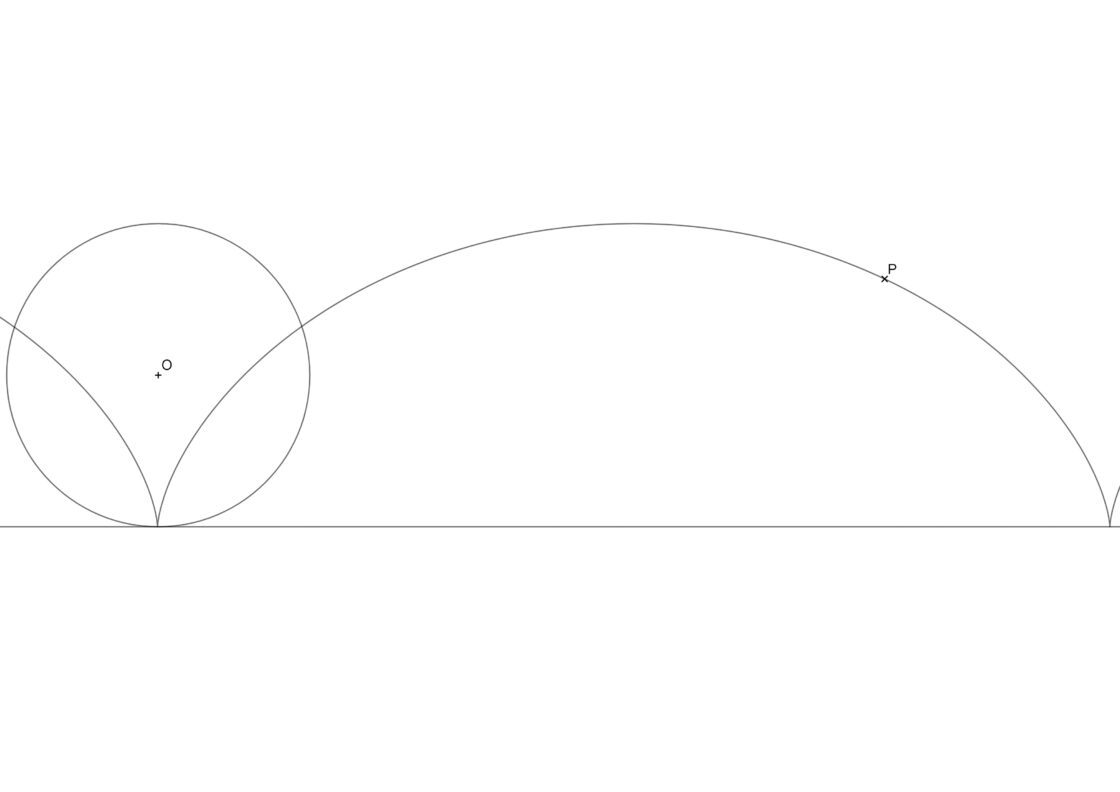
- Traza una paralela a la línea sobre la que rueda la ruleta que pase por el centro O de la ruleta.
- Con centro en P y radio igual al de la ruleta, traza un arco que corte a la paralela que acabas de dibujar. Ese punto de corte es O1, que representa la posición del centro en ese momento concreto.
- Dibuja una perpendicular a la línea sobre la que rueda la ruleta. Donde esa perpendicular corta a la línea base, tienes el punto R.
- Une P con R con una línea. Esa es la recta normal al punto P.
- La recta perpendicular a la normal es la tangente a la cicloide en el punto P.
En la siguiente aplicación puedes mover el punto P para ver como se resuelve la tangente a la cicloide de forma independiente a la posición del punto.
Da igual si se trata de una cicloide alargada o acortada. El procedimiento es el mismo. Lo único que tienes que tener en cuenta es hacer la circunferencia con centro en P con el mismo radio de la distancia de P a O.
