En este tipo de ejercicios de enlaces tienes dos rectas, o una recta y una circunferencia. Lo que te piden es resolver el enlace entre ambas con un arco de circunferencia. Como en todos los ejercicios de enlaces, debes recordar las propiedades básicas de las tangencias. Si las recuerdas, puedes resolver la mayoría de estos problemas por deducción.
Enlace de dos rectas paralelas
El punto de partida son dos rectas paralelas entre si, también conoces un punto de tangencia T. Lo que se pide es realizar el enlace de ambas rectas con un arco de circunferencia a partir del punto T. Este problema es similar a dibujar una circunferencia tangente a una recta. En ese tipo de problemas, el centro de la circunferencia siempre está sobre la perpendicular al punto de tangencia. Así pues, tu punto de partida es parecido a esto:
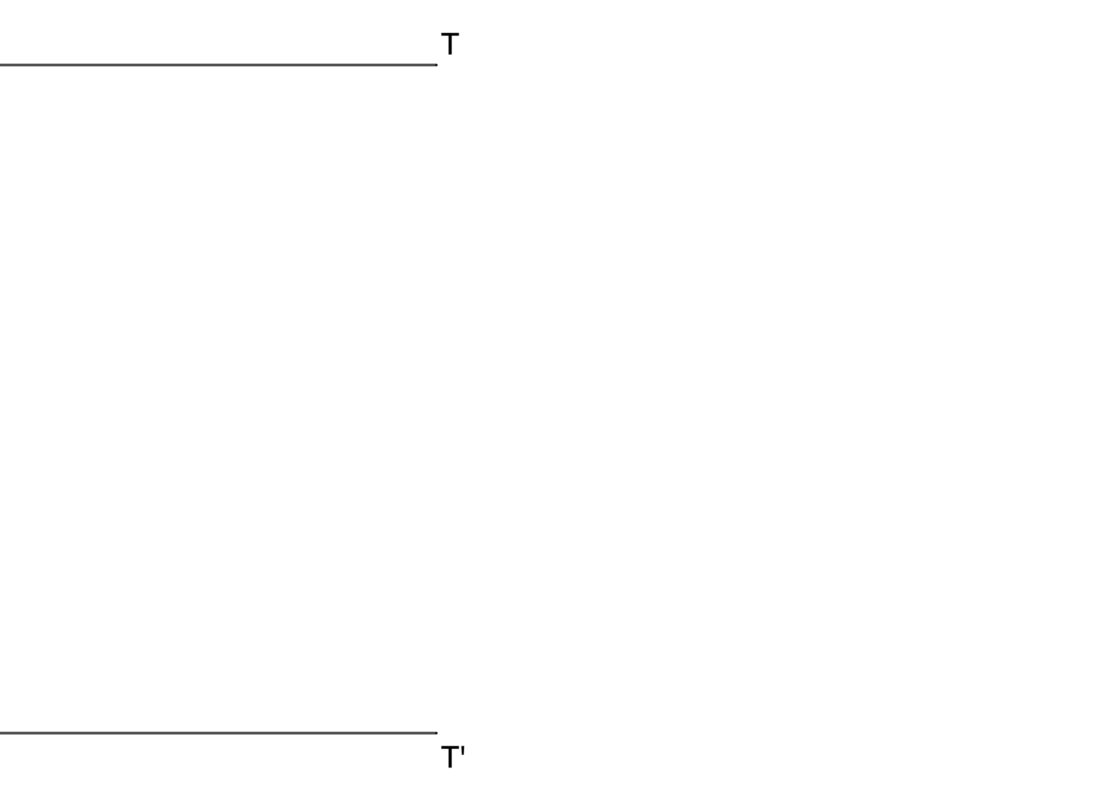
- Empieza por dibujar una recta perpendicular a ambas rectas que pase por T. Recuerda que cuando dos rectas son paralelas, si una recta es perpendicular a una de ellas, también lo es a la otra. El punto donde esa perpendicular corta a la otra recta es el punto T’.
- Esta construcción es simétrica. Eso significa que el centro O va a estar a la misma distancia de T que de T’.
- Dibuja la mediatriz del segmento que forman T y T’ para hallar el centro O.
- Con centro en O y radio hasta T dibuja un arco hasta T’. Esa es la solución que estás buscando.
Enlace de dos rectas que se cortan conociendo el punto de tangencia
Para este problema conoces dos rectas que se cortan, y el punto de tangencia T sobre una de ellas. Lo que te piden es dibujar un arco que una ambas rectas con un enlace. Al igual que en el caso anterior, debes recordar que el centro de la circunferencia tangente está sobre la perpendicular. También es importante recordar que en el caso de dos rectas que se cortan, una circunferencia tangente a ambas siempre tiene el centro sobre la bisectriz. Tu punto de partida se parecerá a lo siguiente:
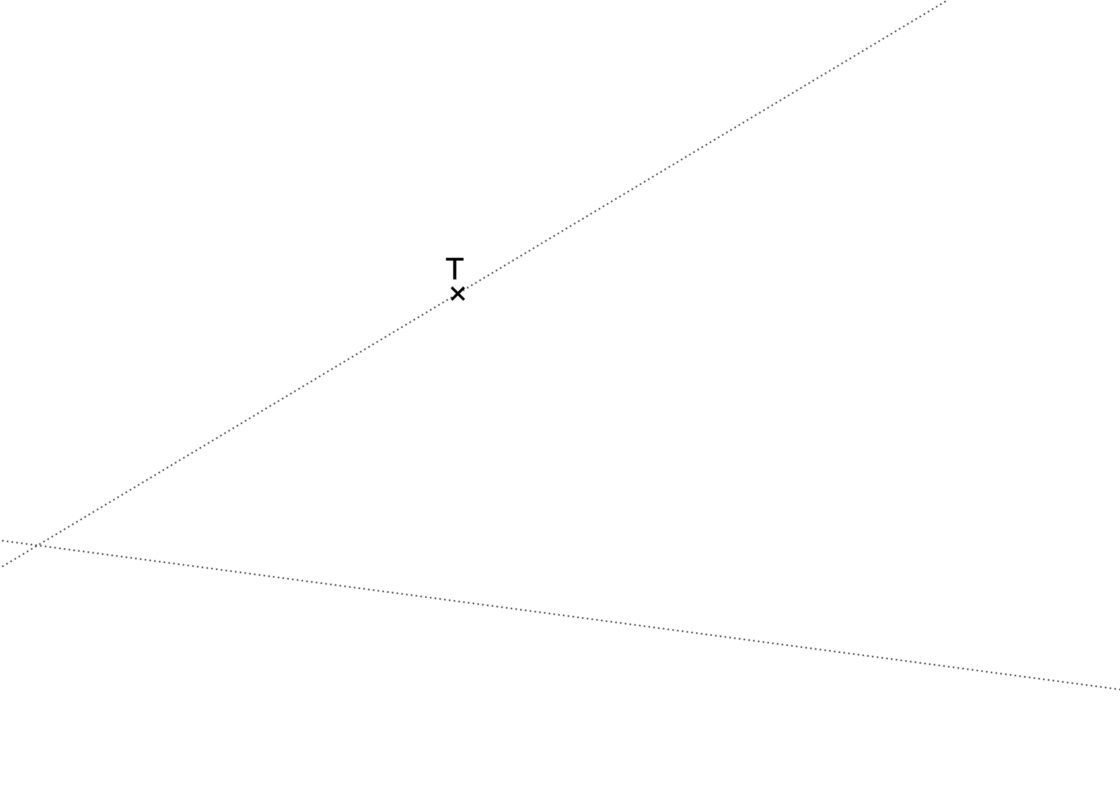
- Dibuja una perpendicular que pase por el punto de tangencia T. No hace falta que sea muy grande.
- Traza la bisectriz de ambas rectas, ya que el centro estará sobre ella.
- El único punto del plano que se encuentra a la vez sobre la perpendicular y sobre la bisectriz es el punto donde se cortan. Ese punto es por tanto O, el centro del arco que debes dibujar.
- Antes de dibujar el arco, halla el punto T’. Para ello solo tienes que dibujar una perpendicular a la otra recta por el centro O. Otra forma posible es dibujar un arco con centro en el vértice y radio hasta T. Ese arco cortará a la otra recta en el punto T’.
- Ahora si, con centro en O y radio hasta T, dibuja un arco hasta el segundo punto de tangencia T’. Esa es la solución que buscas.
Enlace de dos rectas perpendiculares (2 casos)
Problema 1: Conociendo un punto de tangencia
En este caso conoces las dos rectas perpendiculares y un punto T de tangencia. En realidad este ejercicio es exactamente igual que el anterior. La única diferencia es que las rectas forman un ángulo de 90 grados, pero se soluciona de la misma manera y se aplican las mismas propiedades. Tu punto de partida se parecerá a lo siguiente:

- Dibuja una perpendicular que pase por el punto de tangencia T.
- Halla la bisectriz que forman las dos rectas. Una forma fácil y práctica es dibujar un arco con centro en T y radio hasta el vértice. Luego otro arco con centro en el vértice y radio hasta T para hallar T’. Por último, con centro en T’ y radio hasta el vértice. Donde se cortan los arcos de centro T y T’ tienes el centro O.
- Donde la perpendicular y la bisectriz se cortan tienes el centro O del arco que debes dibujar.
- Para hallar el punto T’ tienes que dibujar un arco con centro en el vértice y radio hasta T. Donde corta a la otra recta tienes el punto T’. Si no recuerdas como se hace una bisectriz, puedes hacer una perpendicular por T’. Donde las dos perpendiculares se cortan tienes O.
- Para terminar, dibuja un arco con centro en O y radio hasta T que llegue hasta el segundo punto de tangencia T’. Esa es la solución que buscas.
Problema 2: Conociendo el radio de la solución
La solución es muy sencilla si recuerdas como dibujar cuadrados conociendo el lado. Al fin y al cabo, este ejercicio consiste básicamente en dibujar un cuadrado. Tu punto de partida se parecerá a esto:

- Empieza por dibujar un arco con centro en el vértice y radio igual al que te proporcionan, de esa manera obtienes los puntos T y T’
- Llegados a éste punto tienes dos opciones para hallar el centro O.
- Con centro en T y radio hasta el vértice dibuja un arco. Luego realiza otro arco con centro en T’ y radio hasta el vértice. Donde ambos se cortan tienes el centro O
- La segunda opción es dibujar perpendiculares a las rectas que pasen por T y T’, donde ambas rectas se cortan tienes el centro O.
- Para terminar dibuja un arco con centro en O y radio OT que vaya desde T a T’. Esa es la solución que buscas.
Enlace de dos rectas mediante arcos opuestos e iguales
Para realizar ejercicios de enlaces de este tipo te proporcionan dos semirrectas que se abren en direcciones distintas. También conoces los puntos T y T’ y te piden unir ambos puntos mediante el enlace de dos arcos opuestos. Tu punto de partida se parece a lo siguiente:
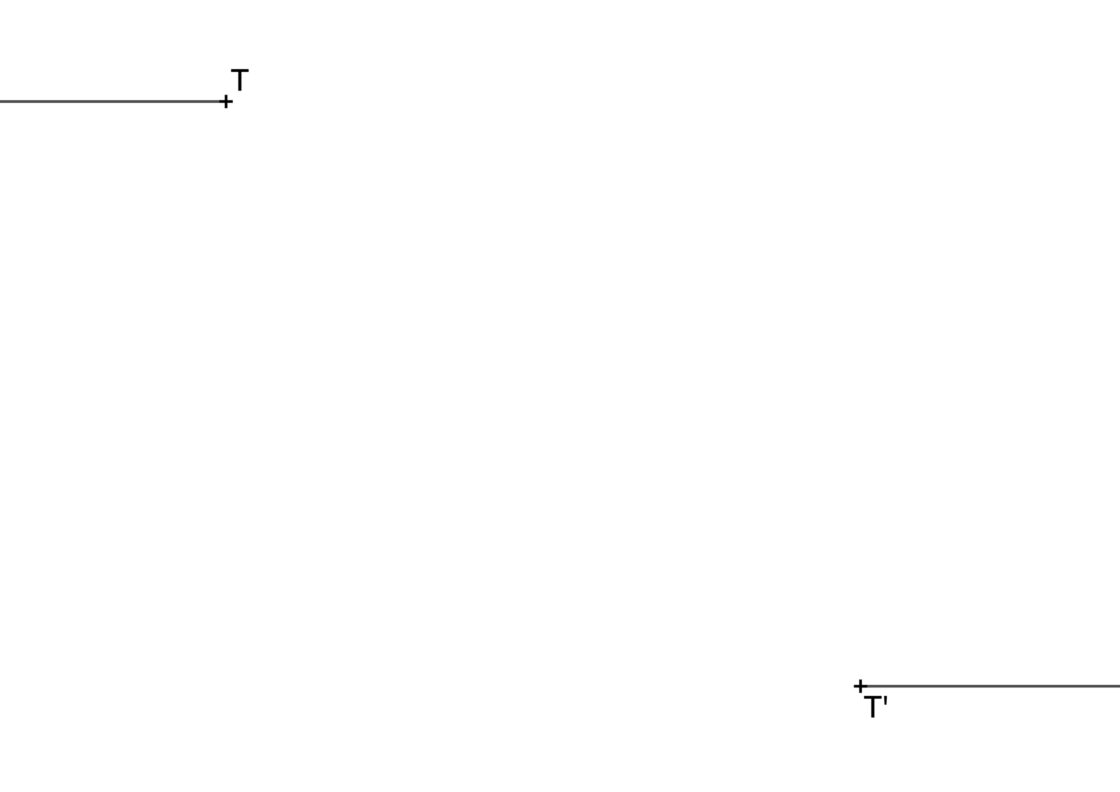
- Empieza por dibujar perpendiculares por T y T’. Como ya sabes los centros estarán sobre esas perpendiculares.
- Une T y T’ con una recta. Dibuja la mediatriz de ese segmento para hallar el punto medio. Ese punto será T2, donde los arcos cambian de dirección.
- Dibuja la mediatriz del segmento que forman T y T2. Donde esa mediatriz corta a la perpendicular que pasa por T tienes el centro O1. Ahora dibuja un arco con centro en O1 y radio hasta T2 que llegue hasta T. Esa es media solución.
- Para hallar el centro O2 tienes dos opciones:
- Dibuja una línea que pase por O1 y T2, donde esa línea corta a la perpendicular que pasa por T’ tienes el centro O2.
- La otra opción es dibujar la mediatriz del segmento que forman T2 y T’. Donde esa mediatriz corta a la perpendicular que pasa por T’ tienes el centro O2.
- Para terminar, dibuja un arco con centro en O2 y radio hasta T’ que vaya de T’ hasta T2. Ese es el otro arco con el que terminas el ejercicio.
Una variante: Cuando conoces un radio
El punto de partida es igual al anterior, pero en este caso conoces uno de los dos radios de la solución, al que llamaremos r1.
- Realiza una perpendicular a la primera línea por T1 y sobre ella mide el radio r1 que conoces. De esa manera hallas O1
- Dibuja la línea que une los dos puntos de tangencia, representados por los extremos de las semirrectas.
- Con centro en O1 y radio r1 traza un arco que corta a la recta anterior en el punto T.
- Dibuja una perpendicular a la segunda línea que pase por T2
- Traza la mediatriz de T2T para hallar en el punto de corte con la recta anterior el centro O2
- Con centro en O2 y radio hasta T dibuja el arco que te falta para completar el ejercicio.
Enlace de una recta y un arco de circunferencia conociendo los puntos de tangencia
Este ejercicio puede ser entre una recta y un arco, o entre una recta y una circunferencia. Es imprescindible que te proporcionen ambos puntos de tangencia, de lo contrario habría infinitas soluciones posibles. El centro de la circunferencia puede ser que no lo conozcas, pero siempre lo puedes deducir usando dos cuerdas de la misma y sus mediatrices. Tu punto de partida debería ser algo parecido a lo siguiente:
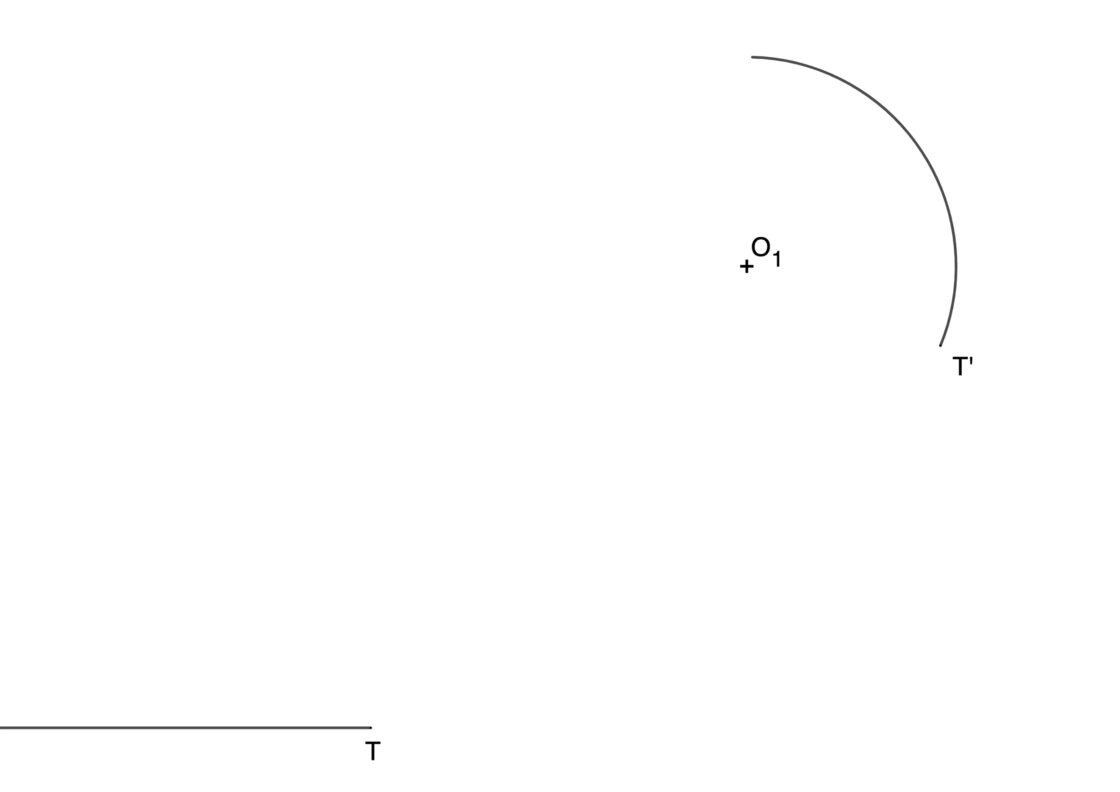
Como siempre, puedes pulsar sobre la imagen para verla a pantalla completa y así imprimirla en un DIN A4 para practicar. A continuación te explico como se soluciona:
- Dibuja la perpendicular a la recta que pase por el punto T. Sobre esa perpendicular se encuentra el centro de la circunferencia que contiene al arco que te falta para completar el ejercicio.
- Une T’ con O1 con una línea y prolóngalo hasta cortar a la perpendicular que acabas de dibujar. El punto donde se cortan es el centro O2 del arco que estás buscando.
- Para terminar, con centro en O2 y radio hasta T dibuja un arco que vaya de T a T’. Esa es la solución que buscas.
Enlace de dos rectas que convergentes con arcos de distinta dirección
Para este ejercicio conoces dos rectas que no son paralelas entre si. También conoces los puntos de tangencia T y T’. Aparte de estos datos te deben proporcionar el radio de uno de los dos arcos, de lo contrario habría infinitas soluciones. El punto de partida sería algo parecido a la imagen siguiente:
Puedes pulsar sobre la imagen anterior para que se abra a pantalla completa y de ese modo imprimirla en un DIN A4 para poder practicar este ejercicio. La forma de solucionar este ejercicio es la siguiente:
- Como sabemos que las circunferencias tangentes a rectas tienen sus centros sobre perpendiculares al punto de tangencia, lo primero que tienes que hacer son perpendiculares a ambas rectas por ambos puntos de tangencia.
- Uno de los radios lo conoces, por lo que si llevas la longitud del radio sobre una de las perpendiculares tendrás uno de los centros. En este ejemplo yo lo he llevado sobre la perpendicular a T’, como puedes ver. De esa manera determinas O1.
- El segundo centro se determina por simetría. Sobre la perpendicular que pasa por T, mide hacia abajo la longitud del radio para determinar el punto P.
- Ahora traza la mediatriz del segmento O1P. Esa mediatriz corta a la perpendicular que pasa por T en el punto O2. Ese es el centro de la segunda circunferencia.
- Dibuja un arco con centro en O1 y radio igual al que te proporcionan.
- Con centro en O2 y radio hasta T dibuja otro arco.
- Si unes con una línea O1 y O2, donde esa línea corta a ambas circunferencias tienes el punto de tangencia T1 donde la curva cambia de dirección.
Enlace de dos rectas paralelas con arcos distintos
Para resolver este problema los datos que conoces son dos semirrectas y los puntos de tangencia T y T’. El punto de partida es el siguiente. Como siempre, puedes pulsar sobre la imagen para abrirla a pantalla completa e imprimirla. Te servirá para practicar este ejercicio.
Se resuelve de la siguiente manera:
- Como en ejercicios anteriores, dibuja perpendiculares que pasen por T y T’, ya que sobre ellas tendrás los centros de los dos arcos.
- Este ejercicio en realidad tiene soluciones infinitas, pero para facilitar la tarea, se suele tomar un punto medio. Es decir, dibuja la mediatriz del segmento que forman T y T’ para hallar el punto medio P.
- Dibuja una recta paralela a ambas rectas que pase por P.
- Con centro en P y radio hasta T, dibuja un arco que corte a la recta que pasa por P en el punto T1. Este punto será el lugar donde se cambia de un arco a otro.
- Halla la mediatriz del segmento que forman T’ y T1. Esa mediatriz corta a la perpendicular que pasa por T’ en el punto O2, centro del arco más pequeño.
- Ahora dibuja la mediatriz del segmento que forman T y T1. Donde esa mediatriz corta a la perpendicular que pasa por T tienes el centro O1.
- Dibuja uno de los arcos con centro en O1 y radio hasta T que llegue hasta T1.
- Para terminar traza el otro arco, con centro en O2 y radio hasta T’ de manera que llegue hasta T1.
