Sección plana de una pirámide de base octogonal con un plano proyectante vertical y verdadera magnitud

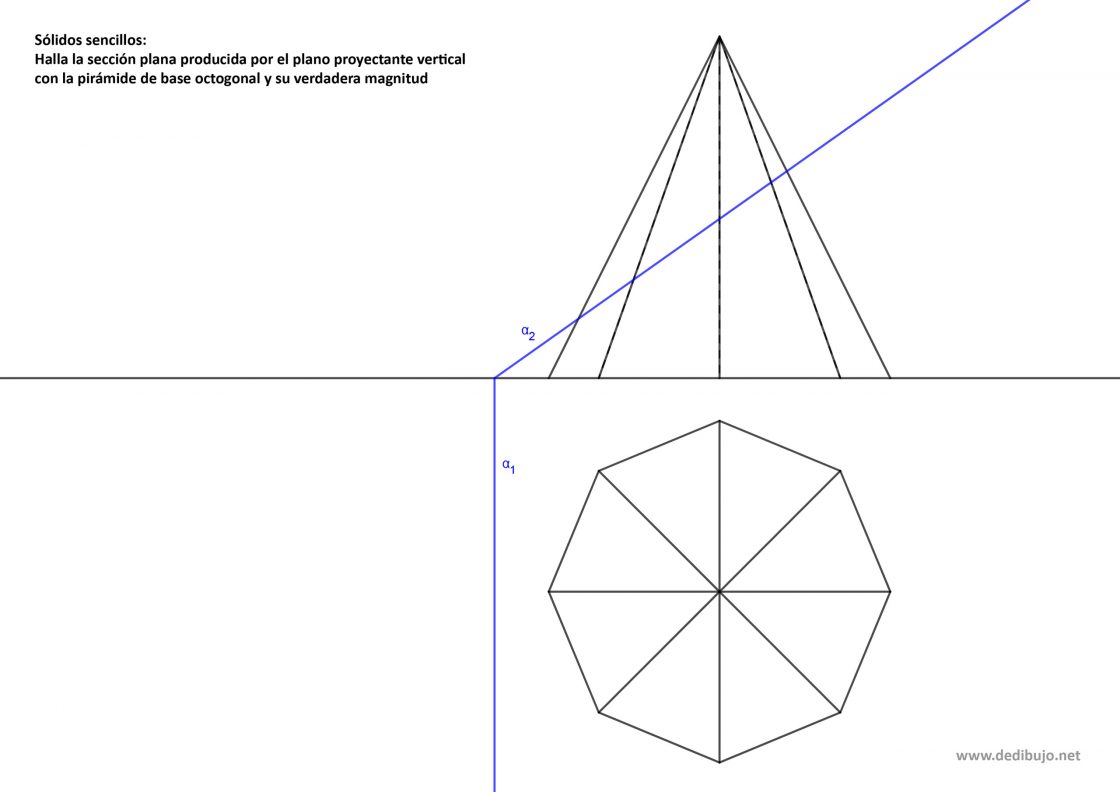
Hallar la sección plana de una pirámide de base octogonal con un plano proyectante vertical, así como su verdadera magnitud es un proceso algo largo. De todas formas, no se trata de un proceso complejo. Te voy a poner a continuación dos posibilidades. En la primera de ellas, ninguna de las aristas es perpendicular al plano vertical, por lo que es algo más sencilla. La segunda opción tiene dos aristas perpendiculares al plano vertical, por lo que para resolverlo debes recurrir a la tercera proyección.

Sección plana de un plano proyectante con con una pirámide de base octogonal en sistema diédrico, y su verdadera magnitud (opción sencilla)

Digo que esta es la opción sencilla porque todas las intersecciones del plano con las aristas de la pirámide se pueden hallar directamente, sin pasos adicionales. Recuerda que al tratarse de un plano proyectante, las intersecciones se pueden hallar directamente en la proyección vertical. Para obtener la correspondencia horizontal, solo hay que trasladar las intersecciones de forma perpendicular a la línea de tierra.

Tu punto de partida es algo parecido a ésto:

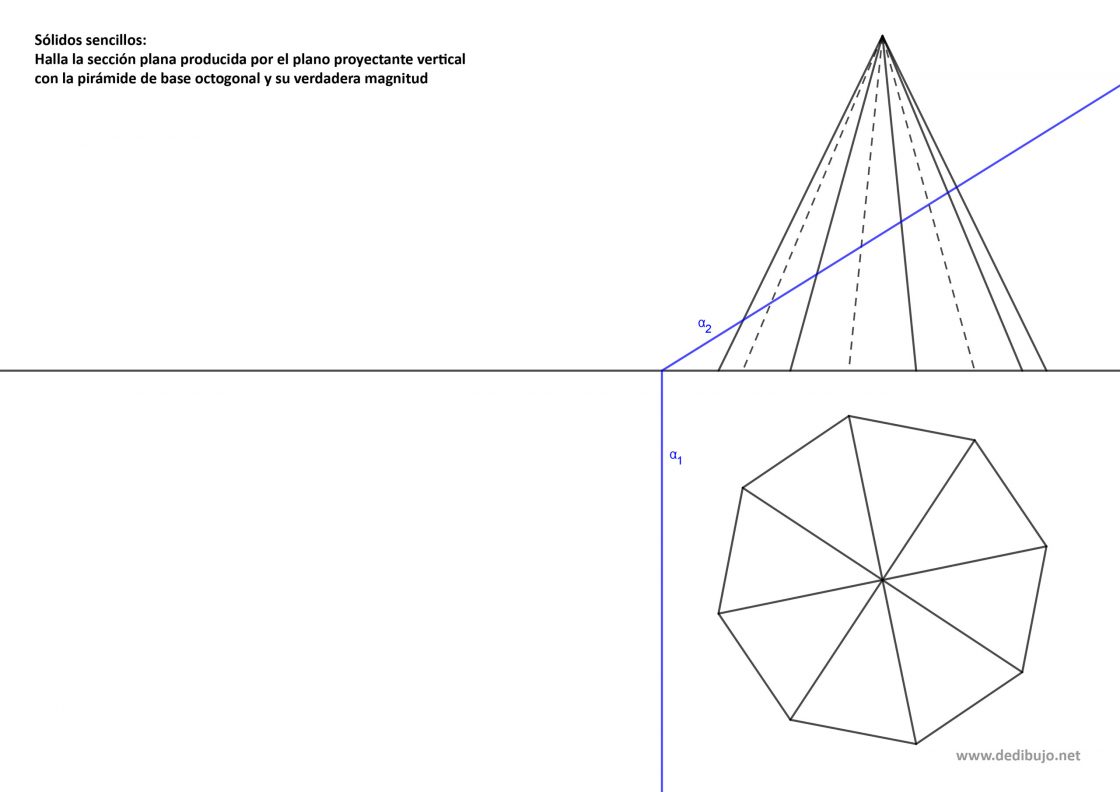
1. Empieza por marcar la intersección de la traza vertical del plano con cada una de las proyecciones verticales de las aristas. Así obtienes A₂, B₂, C₂…
2. Acto seguido dibuja líneas perpendiculares a la línea de tierra que pasen por cada uno de esos puntos. Donde esas perpendiculares cortan a la proyección horizontal correspondiente a cada línea tienes los puntos A₁, B₁, C₁…
3. Uniendo A₁, B₁, C₁… tienes la proyección horizontal de la sección plana.
4. Con centro en O y radio hasta A₂, B₂, C₂… Traza arcos hasta cortar la línea de tierra. A esos puntos puedes llamarlos A, B, C…
5. Para terminar traza perpendiculares a la línea de tierra por A, B, C… y paralelas por A₁, B₁, C₁…
6. Donde esas líneas se cortan tienes los puntos A’, B’, C’… Uniendo todos esos puntos tienes la verdadera magnitud de la sección plana que produce el plano proyectante vertical con la pirámide de base octogonal.

Cuando dos aristas son paralelas al plano de perfil

Esta variante es un poco más complicada porque dos de las aristas de la pirámide se encuentran en un plano paralelo a la proyección de perfil. Por este motivo, para poder solucionarlo es necesario recurrir a la tercera proyección.

Tu punto de partida es semejante a éste: