En el sistema diédrico un plano se representa mediante sus trazas, que son las intersecciones del mismo con los planos de proyección. Es decir, su representación será la de dos rectas, una en el plano vertical y otra en el plano horizontal. Si el plano se llama α estas dos rectas se denominan traza horizontal α1 y traza vertical α2. Con unas pocas excepciones, las dos trazas coinciden siempre en la línea de tierra.
Aquí abajo te dejo una aplicación interactiva para que entiendas como funcionan las trazas del plano. Puedes mover los puntos A y B para ver como se dibuja el plano y sus trazas. Te he incluido también la traza α3 de perfil, que no se suele representar. No obstante considero necesario incluirla aquí para que quede más claro el concepto de los planos en diédrico.
Posiciones particulares del plano
Tal como te comentaba antes, hay determinados planos cuya posición respecto a los planos de proyección tiene características particulares. A continuación vamos a verlos detalladamente.
Plano horizontal
Se trata de un tipo de plano que es paralelo al plano horizontal, por lo que solo tiene traza vertical α2 que además es paralela a la línea de tierra. Se pueden distinguir en el mismo tres posiciones particulares: Cuando se encuentra por encima del plano horizontal, cuando coincide con el mismo y cuando se encuentra por debajo del mismo.
En la aplicación de aquí abajo puedes mover el punto A para ver como se representan las trazas del plano horizontal en diédrico. Puedes moverlo a la línea de tierra y por debajo de ella para ver las tres posiciones particulares.
Plano frontal
Un plano frontal en sistema diédrico es aquel que es paralelo al plano vertical. Por lo tanto solo tiene traza horizontal α1 que es paralela a la línea de tierra. Al igual que pasaba con el plano horizontal, podemos encontrar tres posiciones particulares: Cuando está por delante del plano vertical, cuando está contenido en el plano vertical y cuando se encuentra por detrás del mismo.
Aquí abajo puedes mover el punto A para ver como se comporta la traza horizontal α1 y la traza del plano de perfil α3
Plano proyectante horizontal
Este tipo de planos son perpendiculares al plano horizontal y oblicuos al plano vertical. Su traza vertical será una línea perpendicular a la línea de tierra, mientras que su traza horizontal cortará en ángulo a la línea de tierra. El ángulo que forma el plano proyectante horizontal con el plano vertical se muestra en su verdadera magnitud en la proyección en diédrico. Cualquier punto, línea o figura contenida en este plano tiene su proyección horizontal coincidente con la del plano.
En la siguiente aplicación puedes mover los puntos A y B para ver como se comportan las trazas vertical y horizontal de éste tipo de planos.
Plano proyectante vertical
Este tipo de plano guarda bastante relación con el anterior. La diferencia es que en este caso el plano es perpendicular al plano vertical, por lo que su traza horizontal es perpendicular a la línea de tierra. La traza vertical forma un ángulo con el plano vertical que se ve en verdadera magnitud en la proyección en diédrico. Cualquier punto, línea o forma que se encuentre sobre este plano tendrá su proyección vertical sobre la traza vertical del plano.
Plano paralelo a la Línea de Tierra
De forma independiente a la posición que ocupa este plano, sus trazas son siempre paralelas a la línea de tierra. Dependiendo de donde se encuentren sus trazas, puedes encontrar cuatro tipos distintos de planos paralelos a la línea de tierra.
Plano perpendicular al primer bisector
En este caso se pueden dar dos posiciones particulares. La primera de ellas proporciona dos trazas simétricas respecto a la línea de tierra. Este es el caso de aquí abajo. Puedes mover los puntos A y B1 para ver como se mueven las trazas en este caso. La línea roja representa la dirección que sigue el plano, perpendicular al primer bisector. La línea roja representa la dirección que sigue el plano, que es siempre perpendicular al primer bisector.
En el segundo caso, las trazas también son simétricas respecto a la línea de tierra, pero además son paralelas a la línea de tierra. Aquí abajo tienes una aplicación interactiva para ver como se comportan las trazas. En este caso es más fácil percibir la perpendicularidad de los planos. Aquí abajo puedes mover el punto B1 para ver como se comportan las trazas y el plano.
Plano perpendicular al segundo bisector
Al igual que en el caso anterior, hay dos posibles posiciones. En la primera de ella las dos trazas dibujan una línea. Aquí abajo puedes mover el punto B1 para ver como se comporta el plano y sus trazas.
En el segundo caso las trazas vertical y horizontal son la misma línea al realizar las proyecciones, de forma independiente a la posición que ocupe el plano perpendicular. Aquí abajo puedes mover el punto A y las trazas vertical y horizontal se calcularán de forma automática. Al mover el punto mueves el plano, que siempre es paralelo al segundo bisector.
Plano de perfil
Un plano de perfil es perpendicular tanto al plano horizontal como al plano vertical. Sus trazas son perpendiculares por tanto a la línea de tierra. Cualquier punto, línea o forma contenido en el plano de perfil tendrá sus trazas coincidentes con las del plano. Al ser sus trazas perpendiculares a la línea de tierra no tiene traza en el plano de perfil, ya que es paralelo al mismo.
Plano que pasa por la Línea de Tierra
Este tipo de planos tienen tanto la traza vertical como la horizontal superpuestas a la línea de tierra. Por ese motivo es imprescindible hallar la traza sobre el plano de perfil, para ver su situación real. Aquí abajo puedes mover el punto A para ver como se comporta este tipo de planos.
Representación de planos en diédrico
Hay cuatro formas de representar planos en diédrico. Mediante tres puntos no alineados, con dos rectas que se cortan o con un punto y una recta. El cuarto método es un caso particular del segundo, es decir, a partir de dos rectas paralelas. Para poder continuar es imprescindible que conozcas tanto como se representa el punto en sistema diédrico, como la manera de identificar y representar rectas en diédrico.
Dibujar planos en sistema diédrico conociendo tres puntos no alineados
- Une los puntos de dos en dos para dibujar dos rectas distintas a las que llamaremos r y s.
- Halla las trazas de las rectas r y s.
- Dibuja dos líneas que unan los puntos de corte de las rectas r y s con los planos vertical y horizontal. Esas líneas son las trazas del plano que estás buscando.
Aquí abajo tienes una aplicación interactiva que espero que te ayude a comprender este ejercicio. Puedes mover los puntos A, B y C para mover las trazas del plano. También puedes mover V1 y V2 en la traza vertical. Del mismo modo puedes mover H1 y H2 en la traza horizontal. Dentro de ellos puedes mover S1 y R2, los puntos S2 y R2 se calcularán de forma automática. El punto B y sus trazas se calculan también de forma automática. A la derecha puedes ver como quedaría todo en perspectiva isométrica.
Te recomiendo ponerlo a pantalla completa y hacer zoom sobre cada zona, ya que son demasiados puntos en un espacio muy reducido.
Trazar planos en diédrico a partir de dos rectas que se cortan
Si te das cuenta, el proceso es exactamente igual que en el caso anterior. Tal vez un poco más sencillo, porque en el caso anterior tienes que dibujar las rectas para hallar sus trazas, y aquí ya las tienes dibujadas de partida.
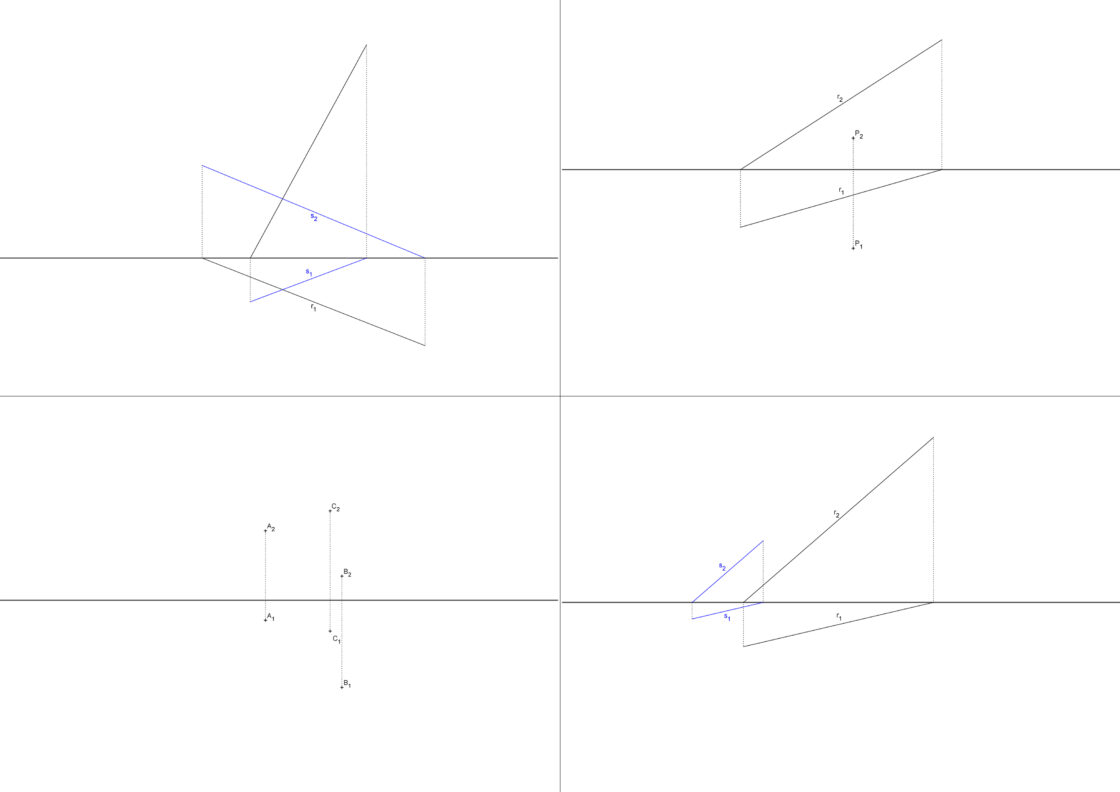
Dibujar un plano en diédrico a partir de una recta y un punto que no pertenece a la misma
Este caso es bastante similar al primero. Lo que debes hacer es marcar un punto cualquiera sobre la recta que conoces. Luego dibujas una línea que pase por ese punto que acabas de marcar y por el otro que te proporcionan. El resto del ejercicio se resuelve igual que el primer caso. Una vez tienes las dos rectas hallas sus trazas y con las trazas hallas el plano.
Aquí abajo los puntos de partida son la recta r, determinada por sus trazas r1 y r2. También se conoce el punto P, representado por sus trazas P1 y P2. El punto R lo he marcado aleatoriamente sobre la recta r. Puedes moverlo para ver que da igual donde esté, el plano siempre es el mismo. También puedes mover las trazas del plano V1 y H2 para modificar las trazas del plano.
Como trazar planos en diédrico a partir de dos rectas paralelas
Lo que debes hacer es convertir esas dos rectas paralelas en dos rectas que si se cortan para poder hallar las trazas. Para ello marca cuatro puntos aleatorios, dos sobre cada recta. Luego los unes formando dos rectas que se cortan. Una vez tienes eso, puedes resolverlo hallando las trazas como en el primer caso.
Determinados tipos de planos son más fáciles de hallar porque las dos rectas paralelas tienen sus trazas tanto sobre el plano horizontal como sobre el vertical. En esos casos solo tienes que unir las trazas directamente para tener la solución.
Aquí abajo tienes una aplicación interactiva de esta última opción. Puedes mover los puntos azules para modificar las trazas de las rectas para ver como cambian también las trazas del plano.
Ejercicios para dibujar planos en diédrico
A continuación tienes una lámina que puedes imprimir para practicar. En ella tienes cuatro ejercicios distintos, uno para cada uno de los problemas típicos que te he explicado más arriba.