Paralelismo entre rectas y planos en sistema diédrico

Lo más habitual en los problemas que te vayas a encontrar referentes al sistema diédrico las rectas y planos tengan posiciones oblicuas entre si. No obstante, en determinadas ocasiones adoptan posiciones de paralelismo o perpendicularidad. Aparte de eso, saber dibujar rectas y planos paralelos o perpendiculares te puede ayudar a resolver algunos problemas comunes en sistema diédrico. En especial son muy útiles a la hora de resolver problemas de distancias entre ellos.

Paralelismo entre rectas

Cuando hablamos de paralelismo entre rectas en sistema diédrico no nos referimos a dos rectas que no se cortan. El hecho de que no se corten no implica que sean paralelas. Dos rectas serán paralelas cuando midiendo la distancia en perpendicular desde una recta a otra, siempre permanece constante de forma independiente al punto que se tome para medir esa distancia.

Así pues, cuando dos rectas son paralelas, sus proyecciones horizontales y verticales son paralelas también entre si dos a dos. En caso de que solo un par fuera paralelo, no estaríamos hablando de rectas paralelas.

Aquí abajo puedes mover los puntos azules para modificar las trazas de las rectas, y sus proyecciones. Date cuenta de que cuando todas sus proyecciones son paralelas, las rectas también lo son.

Para verificar que dos rectas son paralelas entre si, todas las proyecciones de las rectas deben ser paralelas. Por ejemplo, las rectas de perfil tienen las proyecciones vertical y horizontal paralelas entre si. No obstante la proyección sobre el plano de perfil no tiene porqué ser paralela.

Paralelismo entre planos

Dos planos son paralelos en el espacio cuando no se cruzan en ningún punto (dentro o fuera del área de trabajo). Cuando esto ocurre, sus trazas sobre los planos proyectantes serán paralelas entre si. Ten en cuenta que todas las trazas de los planos deben ser paralelas entre si, incluyendo la traza sobre el plano de perfil. Por ejemplo, dos planos perpendiculares al plano de perfil tendrán sus trazas sobre los planos horizontal y vertical paralelos entre si. No obstante sus trazas sobre el plano de perfil no tienen porque ser paralelas. De no ser así, esos planos no serían paralelos.

Aquí abajo puedes mover los puntos para mover las trazas de los planos (y por lo tanto los planos). Fíjate que solo serán paralelos cuando las tres trazas son paralelas entre si.

Como dibujar un plano paralelo a otro que pase por un punto dado

Este es un tipo de problema muy común. Se te proporcionan las trazas de un plano α, α₁ y α₂. También Se te proporciona un punto A representado por sus proyecciones A₁ y A₂. Así pues, tu punto de partida será algo parecido a ésto.

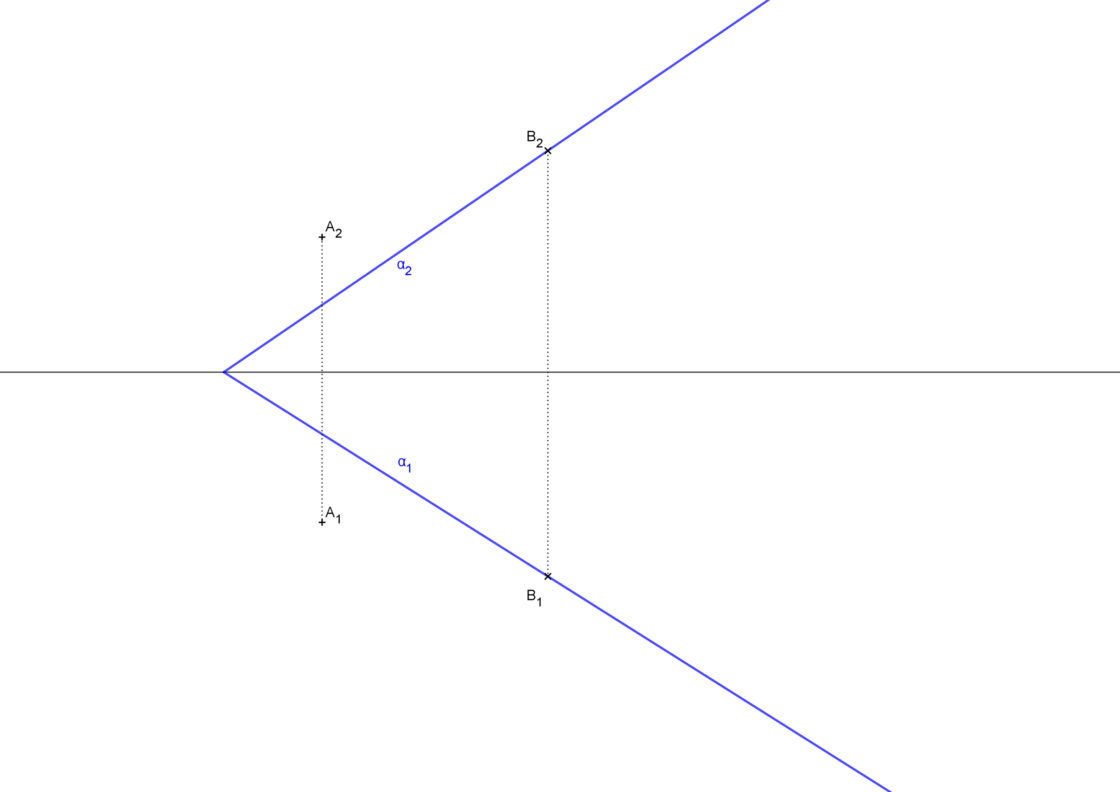
No cometas el error de pensar que haciendo paralelas a las trazas del plano por las proyecciones del punto lo tienes resuelto. Date cuenta de que el punto no se encuentra sobre los planos proyectantes. Si lo vieras en una representación tridimensional sería algo parecido a esto.

Para resolver este problema debes hacer lo siguiente:

1. Dibuja una línea paralela a la traza horizontal del plano que pase por la proyección horizontal del punto. Es decir, una paralela a α₁ que pase por A₁. Donde esa recta corta a la línea de tierra tienes el punto C.
2. Ahora traza una paralela a la línea de tierra que pase por A₂.
3. A continuación dibuja una perpendicular a la línea de tierra que pase por C, y mira donde corta a la paralela que has dibujado en el paso anterior. Ese punto es D.
4. Lo siguiente que debes hacer es trazar una paralela a α₂ que pase por D. Esa será la traza vertical β₂ del nuevo plano β. Donde esa traza corta a la línea de tierra tienes el punto E.
5. Para terminar, dibuja una paralela a α₁ que pase por E. Esa línea será la traza horizontal β₁ del plano paralelo β.

Date cuenta de que lol que has hecho para resolver este ejercicio es dibujar una recta horizontal que pase por A y que esté contenida en el plano β. El punto donde corta al plano vertical te indica un punto de las trazas del plano β. Gracias a este punto puedes hallar ambas trazas.

En realidad, si dibujas una recta contenida dentro del plano α y luego dibujas una recta paralela a esa que pase por el punto A también obtienes dos puntos que pertenecen a las trazas del plano β. Aquí abajo tienes la demostración. Por una parte tienes la solución utilizando un plano proyectante vertical. Las líneas naranjas representan la solución utilizando una recta paralela que pase por P. No obstante, aunque es un método válido, no se suele utilizar porque implica más líneas, más pasos. Es decir, es más complicado.

Paralelismo entre una recta y un plano

Se dice que una recta es paralela a un plano cuando no corta a éste en ningún punto. Ya se que parece absurdo recordarlo, pero no debe cortarlo ni tan siquiera fuera del espacio de trabajo. Si lo corta en algún punto, aunque no puedas verlo, entonces no será paralelo. Otra forma de expresarlo sería decir que para ser paralela al plano, una recta debe ser paralela a una recta contenida dentro de dicho plano. A menos que te impongan algún tipo de requisito más (como que pase por determinados puntos) habrá infinitas soluciones.

Aquí abajo puedes mover los puntos azules para mover tanto el plano como la recta contenida en el mismo y la recta externa. Fíjate que cuando las proyecciones de ambas rectas son paralelas entre sí, la recta es paralela también en el sistema diédrico.

Ejercicio de paralelismo en sistema diédrico; dibujar una recta paralela a un plano que pasa por un punto dado

Para este ejercicio te proporcionan las trazas de un plano y un punto A por el que debe pasar la recta. Date cuenta de que este ejercicio es realmente sencillo, ya que hay infinitas rectas paralelas al plano que pasen por ese punto. Para hallarlo debes dibujar una recta cualquiera contenida en el plano. Una vez tienes las proyecciones de esa recta, debes hacer paralelas a las mismas que pasen por el punto. Tu punto de partida pues será algo parecido a esto.

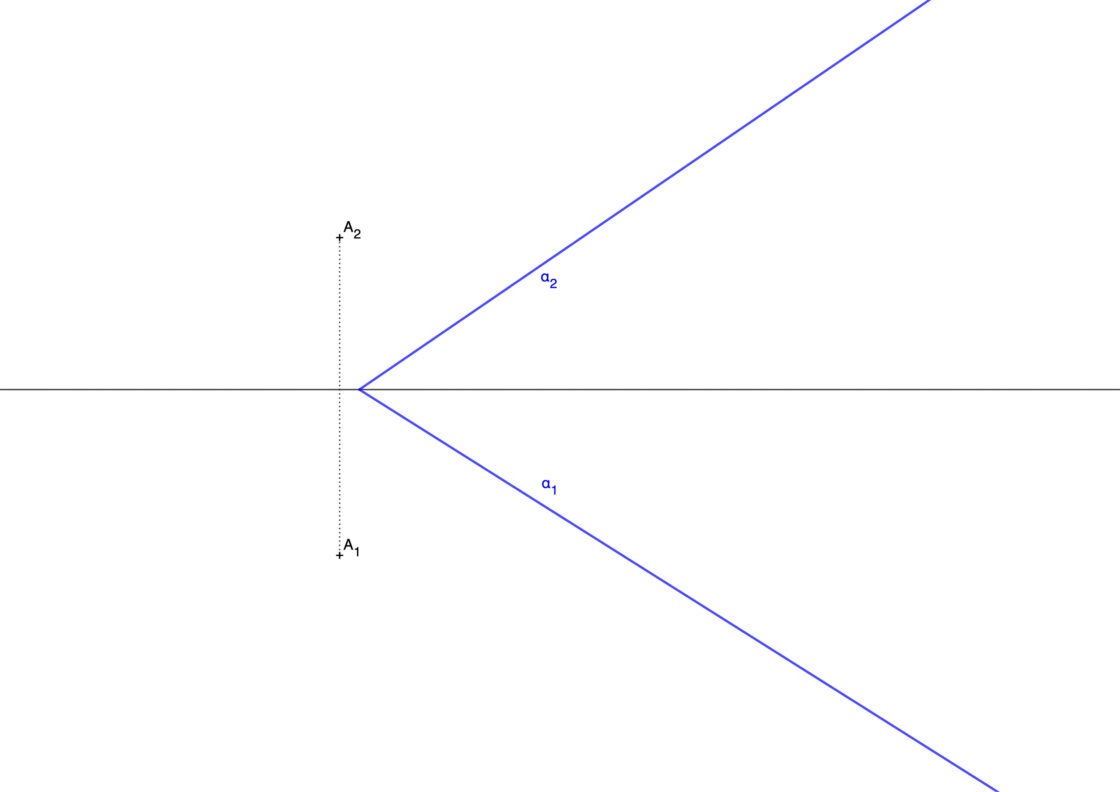
1. Empieza por dibujar una recta cualquiera que corte a la traza vertical del plano en el punto B₂ y a la línea de tierra en el punto C₂.
2. Dibuja una perpendicular a la línea de tierra que pase por el punto C₂. Donde esa perpendicular corta a la traza horizontal del plano tienes el punto C₁.
3. Ahora traza una perpendicular a la línea de tierra que pase por el punto B₂. Donde esa perpendicular corta a la línea de tierra tienes el punto B₁.
4. La línea que une B₂ con C₂ es la proyección vertical de una recta contenida en el plano. Por otra parte, la línea que une B₁ con C₁ es la proyección horizontal de esa misma recta.
5. Traza una paralela a la proyección vertical de la recta que pase por A₂. Esa será la proyección vertical de la recta paralela al plano.
6. Para terminar, dibuja una paralela a la proyección horizontal de la recta que pase por el punto A₁. La recta que has dibujado es la proyección horizontal de la recta paralela.

Como dibujar un plano paralelo a una recta que pasa por un punto dado

Este ejercicio es similar al anterior. En este caso lo que debes hacer es dibujar una recta cualquiera paralela a la que conoces y que pase por el punto. Después dibujas cualquier plano que contenga a esa recta y de esa manera resuelves el ejercicio. Tu punto de partida será algo similar a ésto:

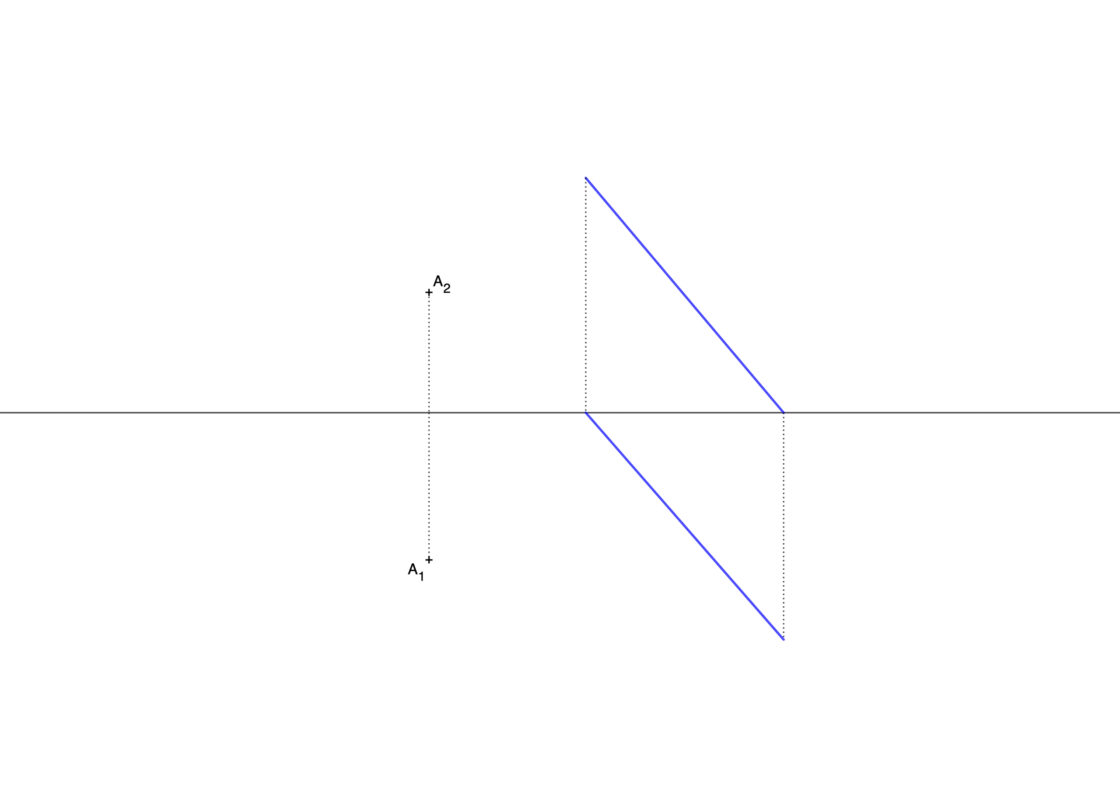
1. Empieza por dibujar una recta paralela a la proyección vertical del plano que pase por A2, Donde esa paralela corta a la línea de tierra tienes el punto B2, que es la proyección vertical de la traza horizontal de esa recta.
2. Ahora dibuja una paralela a la proyección horizontal del plano que pase por A1. Donde esa recta corta a la línea de tierra tienes el punto C1. Ese punto es la proyección horizontal de la traza vertical de la recta
3. A continuación dibuja una perpendicular a la línea de tierra que pase por C1. Donde esa perpendicular corta a la proyección vertical de de la recta tienes el punto C2. Esa es la proyección vertical de la traza vertical de la recta.
4. Continua realizando una perpendicular a la línea de tierra que pase por B2. Donde esa perpendicular corta a la proyección horizontal de la recta tienes el punto B1. Ese punto es la proyección horizontal de la traza horizontal de la recta.
5. Para terminar, marca un punto cualquiera D sobre la línea de tierra. Une el punto D con C2, esa es la traza vertical del plano paralelo. Luego dibuja la línea que une D con B1, esa línea es la traza horizontal del plano paralelo.