Cuando hablamos de hélices en dibujo técnico nos referimos a la curva descrita por un punto que se encuentra sobre una recta. El punto no se encuentra estático sobre la recta, sino que avanza de manera constante sobre ésta. Esta recta, llamada generatriz gira a su vez sobre una línea estática que se denomina eje. Los movimientos alrededor del eje y de la generatriz son proporcionales, de manera que el punto se desplaza una distancia equivalente a la de la recta generatriz en lo que tarda en dar una vuelta de 360 grados alrededor del eje. Los elementos notables de las hélices son:
- Paso: Es la distancia existente entre dos puntos de la hélice que se encuentran sobre la misma generatriz.
- Espira: Se denomina así a cada una de las curvas que describe el punto al dar una vuelta completa sobre la superficie en la que se desplaza.
Trazar una hélice cilíndrica conociendo el diámetro y el paso
El ejemplo más visual de las hélices cilíndricas es un tornillo. En ese caso, el paso es muy pequeño, por lo que las vueltas están muy juntas. En la aplicación de aquí abajo puedes mover el punto P para ver cómo se desarrollan las curvas de las hélices.
Para que no sea tan tedioso realizar este ejercicio, te he preparado una plantilla donde tienes ya desarrollados los pasos del 1 al 3. Así pues, tu punto de partida se parecerá a esto:
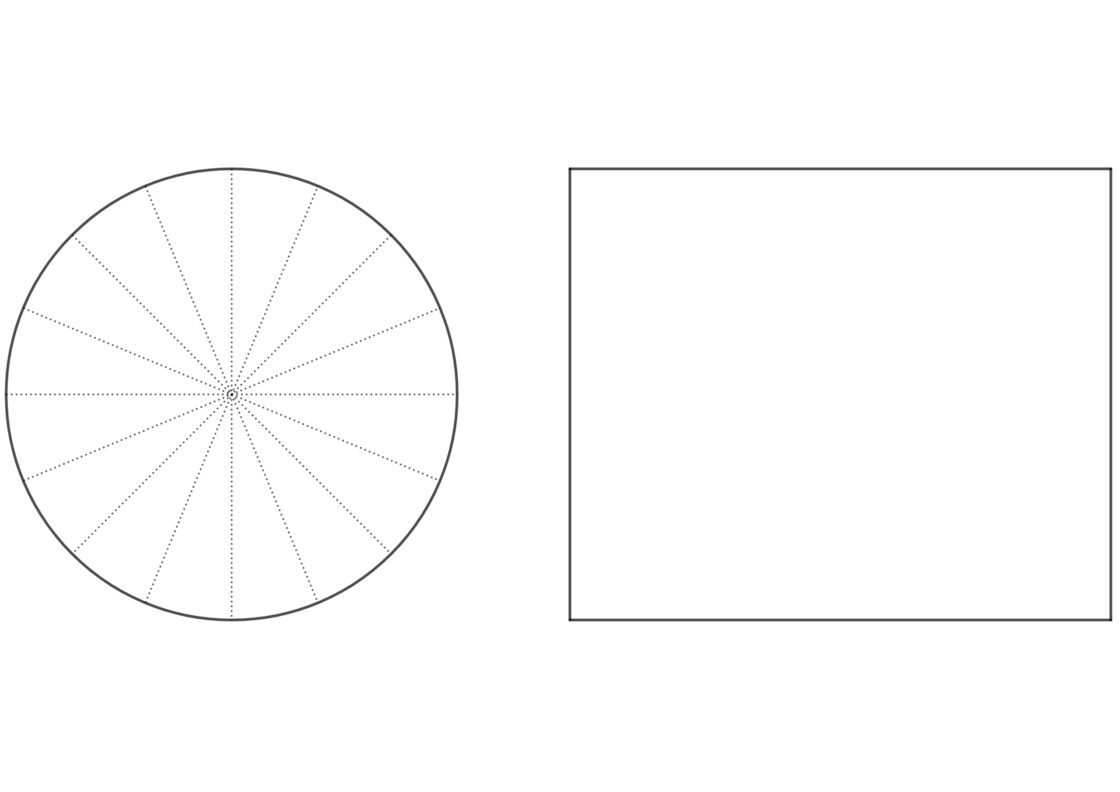
- Empieza por dibujar una circunferencia con el radio que te proporcionan.
- Alineada al lado (o arriba, si lo quieres dibujar en vertical) dibuja un rectángulo que tenga de altura el paso y de ancho el de la circunferencia. Este rectángulo representa el alzado (o el perfil, según cómo lo dibujes).
- Divide la circunferencia en 16 partes iguales usando bisectrices. A cada uno de los puntos que determinan uno de esos sectores llámalo R1, R2, R3…
- Ahora usa el teorema de Tales para dividir la altura del rectángulo también en 16 partes. Cada uno de los puntos que determinan uno de esos segmentos llámalo S1, S2, S3…
- Dibuja paralelas a la base que pasen por S1, S2, S3…
- Traza paralelas a la altura que pasen por los puntos R1, R2, R3… de la circunferencia.
- Donde la paralela que pasa por R2 corta a la que pasa por S2 tienes el punto P2.
- La intersección de la recta que pasa por R3 con la recta que pasa por S3 te permite hallar P3.
- Y así sucesivamente puedes hallar todos los puntos de la hélice.
Como dibujar hélices cónicas sabiendo el paso y la base
Se denomina hélice cónica porque el punto se desplaza sobre la superficie de un cono. Los datos que conoces para solucionar este ejercicio suelen ser el diámetro o el radio de la circunferencia que es la base del cono, y el paso de la hélice, que delimita la altura del cono. Dado que se trata de una figura tridimensional, para poder dibujarla correctamente vamos a necesitar dos vistas, que representarán el alzado y la planta. Aquí abajo puedes mover el punto A1 para ver como se comportan los puntos P1 y P2 que definen la hélice cónica.
Para que no se haga tan largo y tedioso este ejercicio, aquí abajo tienes una plantilla donde ya tienes realizados los pasos del 1 al 4. Tu punto de partida será entonces parecido a esto:
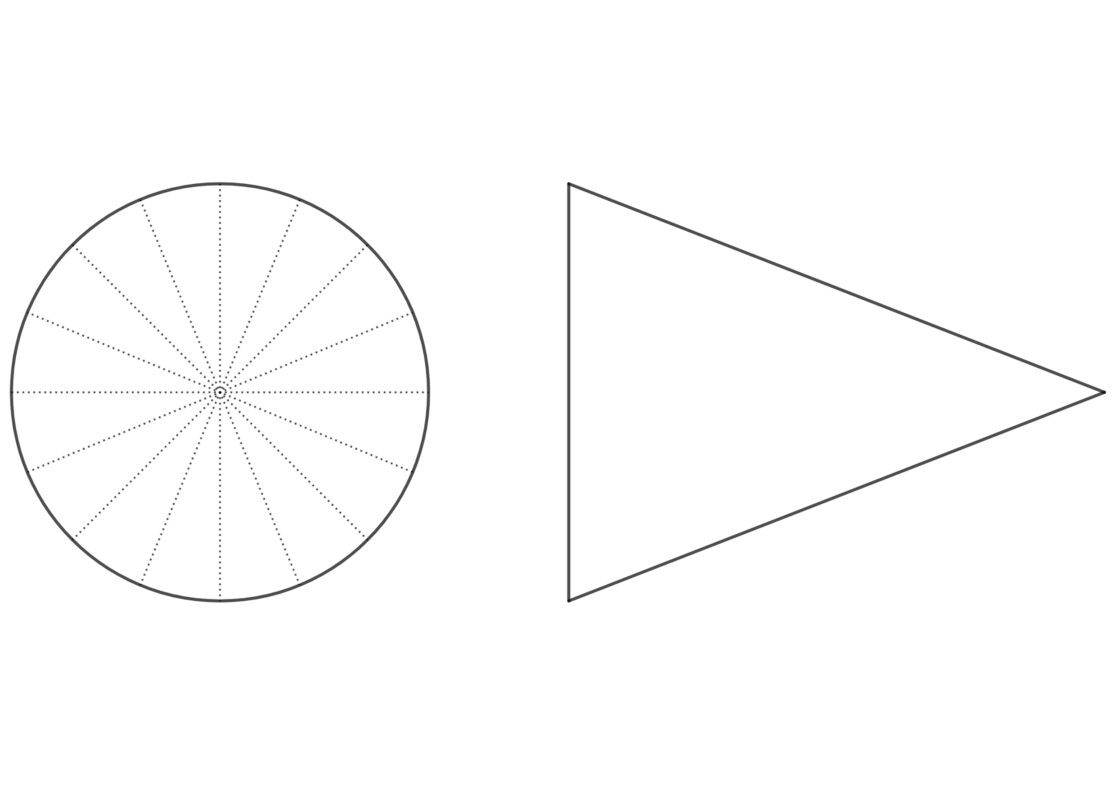
- Utiliza el radio que te proporcionan para dibujar una circunferencia que será la planta. El centro de la circunferencia lo llamaremos O para referirnos a él.
- Dibuja los ejes de esa circunferencia.
- Utilizando bisectrices, divide la circunferencia en 16 secciones iguales. A los puntos que delimitan cada una de esas secciones puedes llamarlos S1, S2, S3… y así hasta el S16.
- Justo al lado del mismo, alineado (o arriba, si prefieres hacerlo en vertical) dibuja un triángulo isósceles cuya base sea el diámetro del círculo, y la altura el paso de la hélice.
- Ahora divide la altura en 16 partes iguales utilizando el teorema de Tales. A cada uno de los puntos de corte que determinan los secciones llámalos A2, A3, A4, y así sucesivamente.
- Por cada uno de esos puntos dibuja una paralela a la base.
- Dibuja perpendiculares a la base del triángulo que pasen por cada uno de los puntos de corte de los sectores que determinan S2, S3, S4, etc. Los puntos donde esas rectas cortan a la base llámalos T2, T3, T4, etc.
- Une esos puntos T2, T3, T4, etc. Con el vértice del triangulo, al que llamaremos A. Date cuenta de que T3 sirve tanto para S3 como para S15. Que T4 sirve tanto para S4 como para S14, y así sucesivamente.
- Donde la línea que va de T2 hacia A corta a la paralela que pasa por A2 tienes el punto P2, también tienes el punto P16 donde corta a la paralela que pasa por A16.
- En la intersección de la línea que va de T3 hasta A con las paralelas que pasan por A3 y A15 tienes los puntos P3 y P15.
- El resto de los puntos los puedes hallar siguiendo el mimo proceso.
Aquí abajo tienes una aplicación interactiva donde puedes ver el proceso. Te recomiendo ponerlo a pantalla completa y hacer zoom sobre cada zona para poder ver mejor los nombres de los puntos.
