Dibujar espirales en dibujo técnico, trazado y definición

En dibujo técnico las espirales se definen como líneas curvas que giran sobre si mismas de manera gradual, alejándose del centro de manera continua y proporcionada. Cualquier espiral está definida por tres valores básicos:

• Paso: El paso se define como la distancia que se aleja la curva del centro en una vuelta completa. También marca la distancia de una vuelta a otra, es decir, entre dos espiras consecutivas.
• Espira: Es la curva que realiza la espiral en una vuelta completa.
• Núcleo: Define el lugar donde empieza la espiral. Los núcleos pueden ser un único punto, pero también pueden ser lineales si son varios centros situados sobre una única recta. También puede darse el caso de los núcleos poligonales, cuando son varios centros que coinciden con los vértices de un polígono.

Trazado de la espiral de Arquímedes

Dibujar una espiral de Arquímedes es un proceso tan fácil como largo. Si quieres dibujarla bien, te recomiendo que emplees como poco un DIN A4 solo para esta espiral. Considera un paso de 10cm, por lo que la circunferencia exterior tendría un diámetro de 20cm. De esa manera la podrás dibujar bien. Si dibujas una espiral más pequeña es fácil que se te mezclen los puntos y acabe siendo bastante caótica.

Para que lo tengas más fácil, aquí te dejo una plantilla que puedes utilizar. Te dejo los pasos del 1 al 4 ya resueltos. Tu punto de partida será parecido a esto:

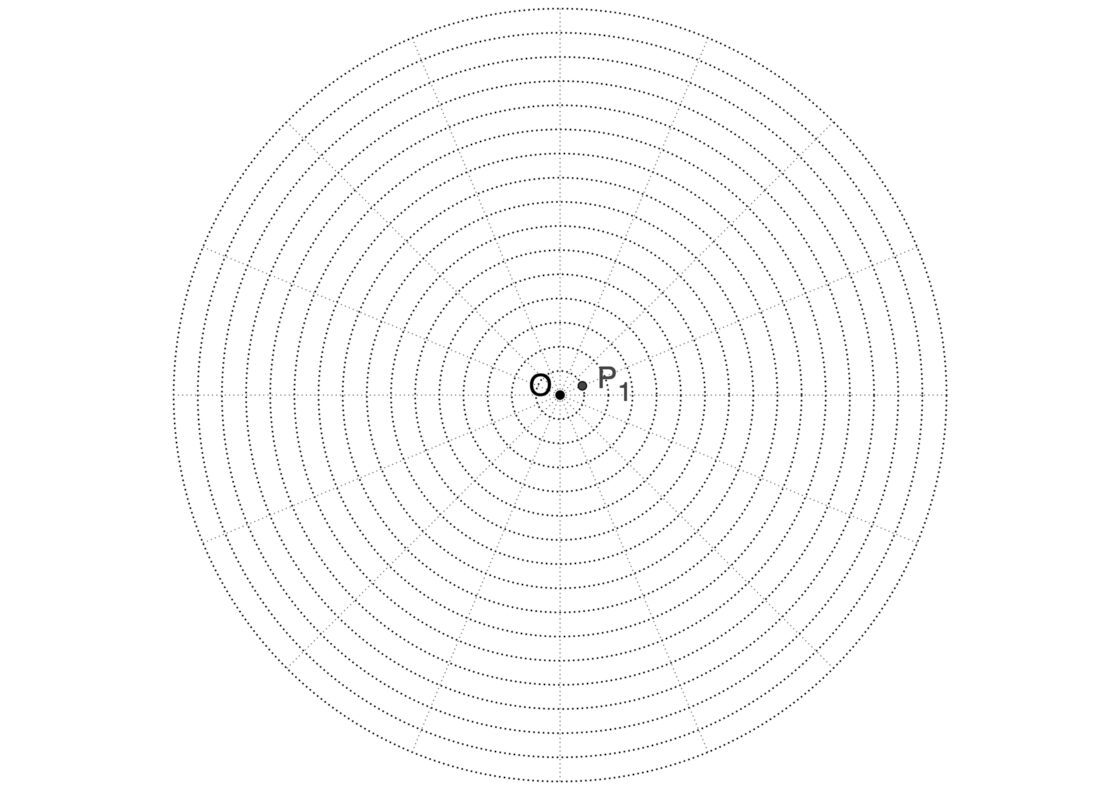
1. Empieza por dibujar la circunferencia exterior. Al centro llámalo O.
2. Dibuja los ejes de la circunferencia. Luego divídelos usando bisectrices hasta obtener 16 segmentos. Cada uno de los extremos de estos segmentos los puedes llamar S₁, S₂, etc.
3. Divide uno de los radios, usando el teorema de Tales, también en 16 partes iguales. Cada uno de los puntos que delimitan una de esas partes puedes llamarlo R₁, R₂, etc.
4. Ahora traza circunferencias de centro O y de radio cada uno de los puntos R₁, R₂, etc. De esa manera tendrás 16 circunferencias concéntricas.
5. Para hallar los puntos de la espiral tienes que ver donde se cruza la circunferencia de radio R₁ con la línea que va hasta S₁. Ese primer punto sería P₁.
6. El punto P₂ estaría en la intersección de la línea que va del centro a S₂ con la circunferencia de radio hasta R₂.
7. Los demás puntos los puedes hallar siguiendo la misma progresión. Aquí abajo tienes la espiral completa por si tienes alguna duda. Te recomiendo ponerlo a página completa y hacer zoom para verlo claro.

Dibujar espirales logarítmicas

Las espirales logarítmicas son un poco peculiares porque el paso no es constante. Es decir, con cada vuelta la distancia entre una espira y otra aumenta de manera proporcional siguiendo una progresión geométrica. Para ponértelo más fácil, aquí tienes una lámina con el triángulo inicial ya dibujado. Tu punto de partida por lo tanto se parecerá a esto:

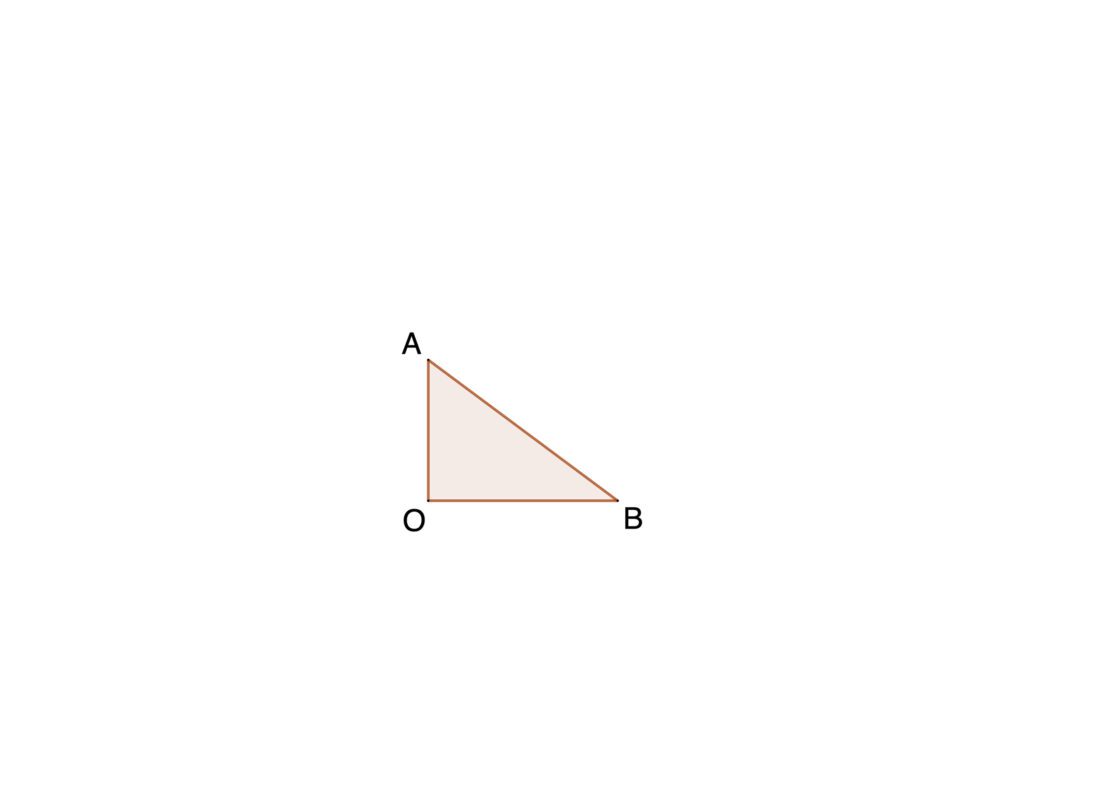
1. Empieza por dibujar dos ejes perpendiculares. Al punto donde se cortan llámalo O.
2. Ahora dibuja un triángulo rectángulo AOB, donde A y B estén sobre los ejes. Ese triángulo será el germen de la espiral logarítmica y definirá su forma. Ten en cuenta que si el segmento OA es más grande que el segmento OB será una espiral decreciente. Si OB es más grande, entonces la espiral se hará cada vez más grande.
3. Dibuja una perpendicular al segmento AB que pase por B. Donde esa perpendicular corta al eje tienes el punto C.
4. Traza la bisectriz del ángulo que forman ABC.
5. Realiza la mediatriz de AB y comprueba donde corta a esa bisectriz. Ese punto es O₁. Con centro el O₁ y radio hasta A, traza un arco de A hasta B.
6. Para continuar, marca una perpendicular al segmento BC que pase por C. Donde corta al eje tienes el punto D.
7. A continuación dibuja la bisectriz del ángulo BCD. Esa bisectriz corta a la de antes en el punto O₂. Con centro en O₂ y radio hasta B, traza un arco de B a C.
8. Supongo que ya has entendido como se continua. Una perpendicular al segmento CD que pase por D te proporciona E. Bisectriz de CDE y donde corta a la de antes tienes O₃. Con centro en O3 y radio hasta E dibujas el arco.

Date cuenta de que las bisectrices de los triángulos que forman las espirales logarítmicas son paralelas entre si. Una vez que ya has hallado las dos primeras, las demás las puedes solucionar trazando paralelas a las que ya tienes.