La afinidad en geometría representa una relación de semejanza entre dos figuras. Se trata de una transformación anamórfica, es decir, que la figura resultante no tiene la misma forma que la figura original. Es una relación de homología con el centro impropio. Esto significa que el centro está infinito, y que por tanto los puntos homólogos siguen una dirección fija. Aparte de anamórfica es homográfica, y cumple las siguientes propiedades:
- Dos puntos afines, A-A’ por ejemplo, siempre se encuentran unidos por una recta que es paralela a una dirección concreta que se llama dirección de afinidad.
- Las rectas que son afines entre si, siempre se cortan en un punto común que se encuentra sobre el eje de afinidad.
- El eje de afinidad se encuentra definido por todos los puntos que son afines de si mismos.
- En una relación de afinidad no existen rectas límite, al contrario que en la homología.
Coeficiente de afinidad
El coeficiente de afinidad es una propiedad más muy interesante. Es un número fijo que viene determinado por un par de puntos afines entre si, y el punto en que corta al eje la línea que los une. En la aplicación interactiva de más abajo tienes la explicación matemática. Puedes mover los puntos para verificar que siempre se cumple.
Para ponerlo en palabras, y utilizando la aplicación que te digo, Si divides el tamaño del segmento QB’ entre el tamaño del segmento BQ obtienes el coeficiente de afinidad k. Este número será constante para cualquier par de puntos. Por ejemplo, si divides RC’ entre CR obtendrás el mismo número. Ojo que no es un número universal como el número pi o el número de oro. En cada ejercicio que resuelvas, el coeficiente de afinidad será distinto.
¿Por que QB’, RC’, SA’y TD’ son negativos?
Ten en cuenta que esos valores son negativos porque se encuentran al otro lado del eje de afinidad. Date cuenta de que el eje de afinidad representa la distancia cero. Por tanto el valor es positivo en dirección a los puntos originales, y negativo al otro lado del eje. Esto da lugar a las siguientes situaciones:
- Si la dirección es perpendicular al eje y k es igual a -1, estamos ante una relación de simetría axial.
- Cuando k es positivo, entonces tanto la figura original, como la afín, se encuentran en el mismo lado del eje.
- En las situaciones en k es igual 1, la figura afín y la original serán la misma.
En la siguiente aplicación interactiva puedes mover los puntos azules para comprender como funciona la afinidad y verificar sus propiedades.
Como dibujar una figura afín a un polígono irregular
En el siguiente vídeo te explico como dibujar la figura afín a un polígono irregular cuando lo que conocemos es una pareja de puntos afines E-E’ en este caso, y el eje de afinidad. Tu punto de partida será algo similar a ésto:
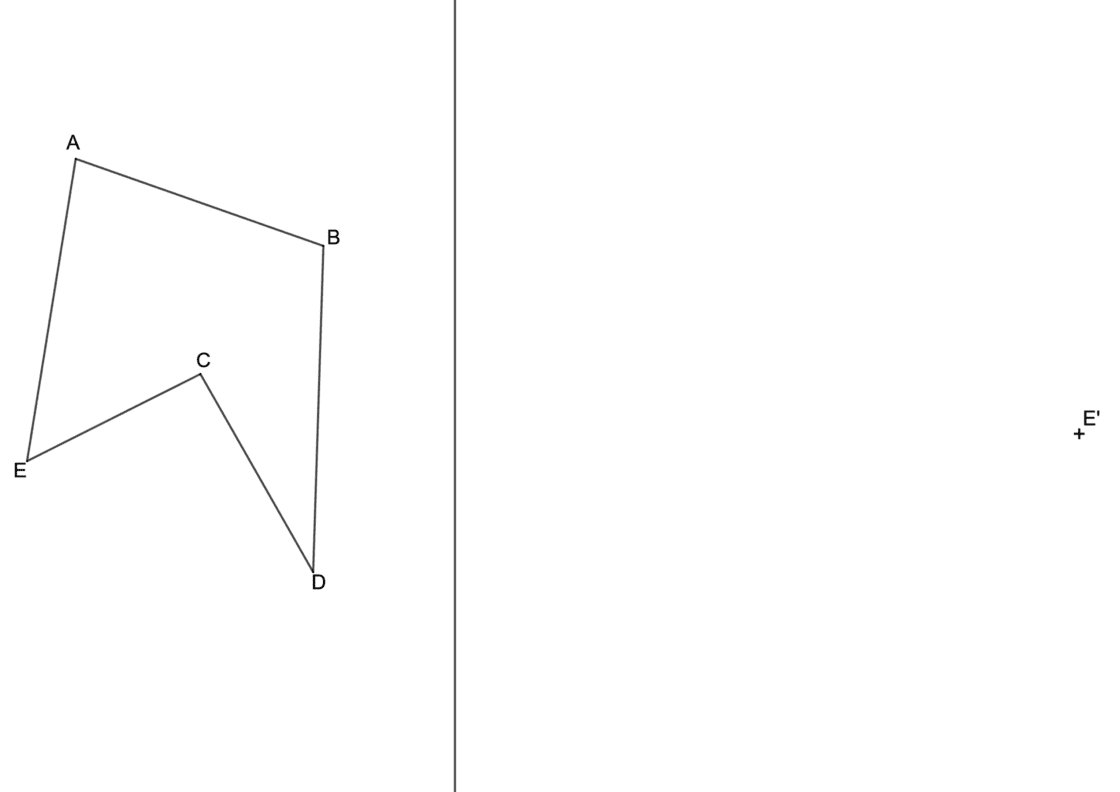
- El primer paso es determinar la dirección de afinidad. Para ello, dibuja la línea que une E con E’
- Ahora dibuja rectas paralelas a esa recta que acabas de dibujar por A, B, C y D.
- Como solo conoces E’, el siguiente punto que debes hallar debe ser uno que forme una recta con E’. En este ejemplo vas a hallar el punto D’. Para ello tienes que trazar una recta que pase por E y D hasta cortar al eje. El punto donde corta al eje llámalo R.
- Une R con E’ y comprueba donde corta a la paralela que pasa por D. Ese punto es D’.
- El siguiente punto que hallaremos será el punto C’. Para ello tienes que prolongar el segmento EC hasta cortar al eje. El punto donde corta llámalo S.
- Une S con E’ hasta cortar a la paralela que pasa por C. Ese punto de corte es C’.
- Cuantos más puntos tienes, más fácil es resolverlo, porque puedes unir con los puntos que acabas de hallar. Te voy a poner un ejemplo, vamos a hallar el punto B utilizando C. Dibuja una línea que pase por C y B hasta cortar al eje. Ese punto de corte llámalo T.
- Ahora une T con C’ con una recta. Donde esa recta corta a la paralela que pasa por B tienes el punto B’.
- Solo falta ahora hallar el punto A’ para terminar la figura afín. Para ello puedes tomar como referencia el punto B. Prolonga la línea que une A con B hasta cortar al eje. Ese punto de corte puedes llamarlo V.
- Dibuja una línea que pase por V y B’ y prolóngala hasta cortar a la paralela que pasa por A. Ese punto de corte es A’.
- Por último, ahora que tienes todos los puntos de la figura afín, solo tienes que unirlos para obtener el resultado.
Por si acaso todavía tienes dudas de como se resuelve, aquí te dejo un vídeo donde puedes ver todo el proceso paso a paso.
Figura afín a una circunferencia
La figura afín a una circunferencia es una elipse. En los enunciados más típicos tienes el siguiente caso; una circunferencia, el eje de afinidad, y una pareja de puntos afines A-A’. También es habitual que la pareja de puntos que proporcionen sean los centros de ambas figuras O y O’. Tu punto de partida será semejante a ésto:
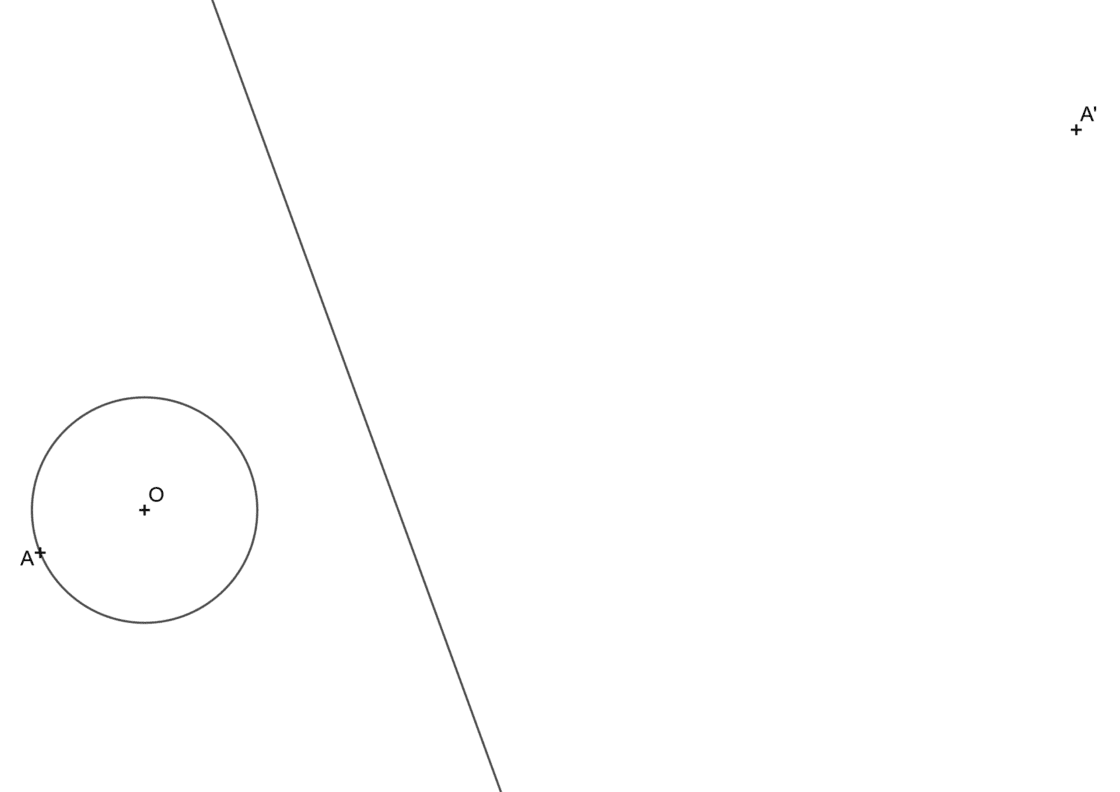
- Dibuja una línea que una A con A’. Esa recta determina la dirección de afinidad, además, donde esa recta corta a la circunferencia tienes el punto B.
- Ahora dibuja una recta perpendicular a esa recta que acabas de dibujar y que pase por el centro O de la circunferencia. Esa perpendicular corta a la circunferencia en los puntos C y D.
- El siguiente paso es dibujar las bisectrices de las dos rectas que acabas de dibujar. Donde esas bisectrices cortan a la circunferencia tienes los puntos E, F, H e I.
- Lo siguiente que debes hacer es dibujar paralelas a la dirección de afinidad que pasen sobre los puntos que has marcado en la circunferencia. Sobre esas paralelas estarán los puntos afines.
- Puedes hallar los puntos en cualquier orden, siempre que empieces uniéndolos con los que conoces. En este caso me refiero al punto A’. Para este ejemplo vas a empezar hallando C. Así pues, dibuja una recta que pase por A y C y prolóngala hasta cortar al eje. Donde esta recta corta al eje tienes el punto R.
- Une R con el punto A’ con una recta. Donde esa recta corta a la paralela que pasa por el punto C tienes el punto C’.
- Como te decía en el ejercicio anterior, cuantos más puntos hallas, más fácil se hace continuar. Ahora que conoces el punto C’, puedes usarlo para hallar otros puntos. En este caso puedes usarlo para hallar el punto E’. Para ello dibuja una línea que pase por E y C hasta cortar al eje. Donde esa línea corta al eje tienes el punto S.
- Traza una recta que pase por S y C’ y prolóngala hasta cortar a la paralela que pasa por E. En ese punto de intersección tienes el punto E’.
- El siguiente punto que vas a hallar será el punto F. Realiza una línea que una A y F y prolóngala hasta cortar al eje. El punto de corte llámalo T.
- Para hallar F’ tienes que unir T con A’ con una recta. Donde esa recta corta a la paralela a la dirección de afinidad que pasa por el punto F tienes el punto F’.
- Ahora vamos a encontrar el punto B. Dibuja una recta que pase por C y B. Donde esa recta corta al eje tenemos el punto U.
- Traza el segmento que une U con C’, donde ese segmento corta a la paralela a la dirección de afinidad que pasa por B tienes el punto B’.
- A continuación vamos a hallar el punto I’. Para ello dibuja una línea que pase tanto por E como por I y prolóngala a cortar el eje. Ese punto de corte llámalo V. Une V con E’ usando una línea. Donde esa línea corta a la paralela que pasa por I tienes el punto I’.
- Para poder dibujar el punto D’ puedes usar como referencia el punto B. Traza una línea que una D con B y corta con ella al eje. Ese punto de corte es W. Si unes W con D’ con una línea, el punto de corte de esa línea con la paralela que pasa por D tienes el punto D’.
- Ya solo queda hallar el último punto, H’. Dibuja una línea que pase por H y F de manera que corte al eje. Ese punto de corte es Y. Ahora une Y con F’ y prolóngalo hasta cortar a la paralela que pasa por H. Donde esas dos rectas se cortan tienes el punto H’.
- Por último para terminar solo tendrías que unir todos esos puntos usando una plantilla de curvas.
Aquí abajo tienes una aplicación interactiva para ver como se construye y como se comporta la construcción dependiendo de la posición del punto A’.
Supongamos que te proporcionan un punto P que pertenece a la circunferencia y su punto afín P’, pero que ambos no están alineados con el centro de la circunferencia. Lo primero que debes hacer es hallar puntos alineados para facilitarte la tarea. Para ello:
- Dibuja la línea que une P con P’, ya que esa línea define la dirección de afinidad.
- Traza una paralela a esa dirección de afinidad que pase por el centro O.
- Donde esa paralela corta a la circunferencia tienes los puntos A y B.
- Utilizando P puedes hallar tanto A’ como B’.
- A partir de aquí lo podrías solucionar como en el ejemplo anterior.
